O que são equações diferencial com variáveis separáveis?
Equação diferencial com variáveis separáveis é uma equação diferencial que
pode ser colocadas na forma;
f(y)dy=g(x)dx
Na maioria das vezes as equações diferencias não são dada na forma
f(y)dy=g(x)dx teremos de recorrer a algumas operações básicas da matemática
para poder colocar a equação na forma f(y)dy=g(x)dx.
Exemplos de equação de diferencial com variáveis separadas

Como resolver uma equação de
diferencial com variáveis separadas?
Tendo já separa as variável ou seja coma equação já na forma f(y)dy=g(x)dx
para resolver se torna muito simples pois para resolver basta integrar ambos
membros.
Resolução de exercícios de equações diferencias com variáveis separadas
a) Resolva a seguinte equação diferencial; (x+x²)dx+ydy=0
Resolução da equação diferencial
(x+x²)dx+ydy=0
Para resolver essa equação diferencial vamos passar o (x+x²)dx para o
segundo membro de mondo que a equação fique na forma f(y)dy=g(x)dx.
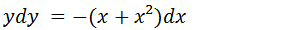
Vamos integrar ambos membros
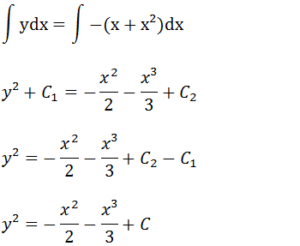
Nota ; C1 e C2 são constantes a diferença de duas constantes resulta em uma
constante.
b)Determine a solução da equação diferencial; x³ yy’+1=y²
Resolução
x³ yy’+1=y²
A equação diferencial acima é uma equação diferencial com variáveis
separada Vamos fazer operações matemáticas de modo a colocar a equação na forma
f(y)dy=g(x)dx e depois integral ambos membros de modo a ter a solução da
equação diferencial
x³ yy’=y²-1
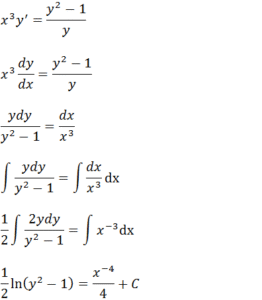
Vamos multiplicar por dois depois isolarmos o y².
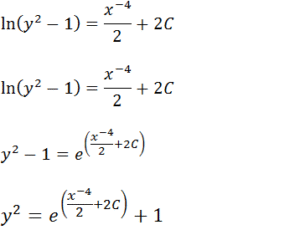
c)Encontre a seguinte equação diferencial; (x+1) y’+y+3=0
Resolução
(x+1) y’+y+3=0
Vamos passar y+3 para o segundo membro
(x+1) y’=-(y+3)
Para facilitar vamos colocar y’ na forma dy/dx
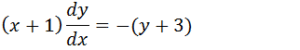
Vamos passar o dx para o segundo membro
(x+1)dy=-(y+3)dx
Vamos passar y+3 para o primeiro membro e x+1 para o segundo membro
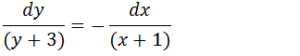
Vamos integrar ambos membros
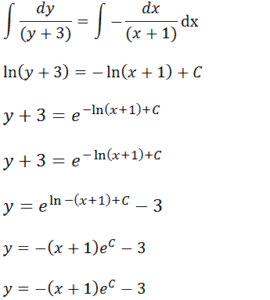

Resolução
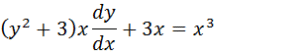
Estamos diante de uma equação diferencial com variáveis separadas para
resolver vamos para o 3x para subtrair no segundo membro, de seguida passar o x
para dividir no segundo membro dor fim passar os dx para o segundo membro para
que a equação diferencial fique na forma f(y)dy=g(x)dx e por fim para resolver
a equação diferencial vamos integral ambos membros
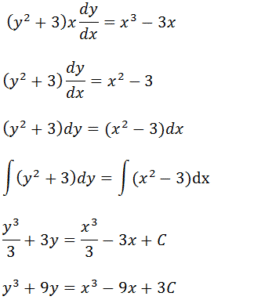
Em alguns casos será necessário determinar o valor da constante C na
solução da equação diferencial

Resolução
Primeiro vamos resolver a equação diferencial e por fim
vamos usar a condição iniciar y(0)=4 para determinar o valor da constante
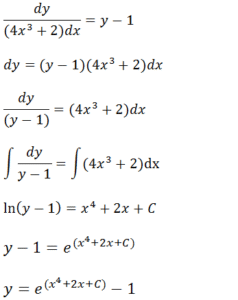
Agora a partir da condição inicial (y(0)=4) vamos determinar o valor de C
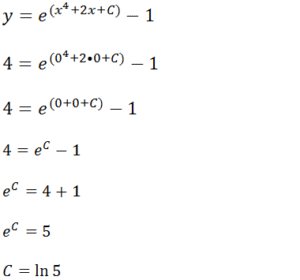
Então a solução da equação diferencial fica ;
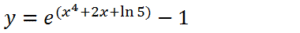
Exercícios sobre equações diferenciais com variável separada para praticar
a) Ache a solução da seguinte equação diferencial (x+2x³+3)dx+y²dy=0
b) Ache a solução da seguinte equação diferencial x³y²y’+4=5y³
c)Resolva a seguinte equação diferencial; (2x²+1) y’+2y=5

f) Ache a soluça da seguinte equação diferencial (x+2x³+3)dx+y²dy=0, y(0)=2
g) Ache a soluça da seguinte equação diferencial 2x³y’+x=5x , y(1)=4
Veja mais uma das nossas aulas
→Classificaçãode uma equação diferencial
→Equação diferencial com variáveis separáveis
→ Aplicação de equações diferencias na física
→ Aulas de Matemática
