1. A formula de passagem da escala Celsius (℃) para escala Fahrenheit (℉) para medir a temperatura ambiente tem a formula linear F=aC+b, (a e b são os coeficientes constantes) sabe se que 0℃ corresponde 32℉ e 100℃ corresponde a 212℉. Qual e a temperatura de um ambiente na escala Fahrenheit se na escala Celsius o seu valor e 50℃
A. 87 B 98 C 118 D 122 E 147
A conversão de temperatura da escala Celsius (℃) para escala Fahrenheit (℉) é feita a partir da fórmula;
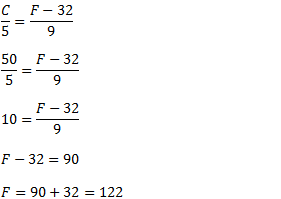
Resposta a temperatura de um ambiente na escala Fahrenheit se na escala Celsius o seu valor e 50℃ é de 122℉.
2. O conjunto (C|R) ∩ T corresponde ao diagrama de Venn, na figura a direita onde T- triangulo R-rectangulo, Círculo
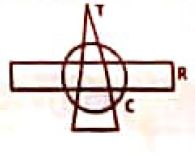

Resposta O conjunto (C|R) ∩ T é a alternativa E.
3. O intervalo de tempo médio estático de uma reacção de um motorista de um carro para começar a travagem extra encontrado de repente um obstáculo no caminho e aproximadamente [1,5; 1,8] segundos, qual o intervalo de distância (em metro) que o percorre carro durante esse intervalo do tempo, se sua velocidade for de 60km/h ?
A. [7; 10] B [11; 17] C [18; 24] D [25; 30] E [31; 43]
O intervalo de distancia será [{d1; d2]
t1=1,5s
t2=1,8s
v=60km/k=50/3 m/s
d1=v•t1=50/3 •1,5=25m
d21=v•t2=50/3 •1,8=30m
Resposta o intervalo de distância é [25; 30]
4. Seja Z1=x1+iY1 e Z2=x2+iY2 dois números do conjunto dos números complexos C . Então Z1>Z2 se
A. ∀x1,x2 ∈ R; y1>y2 B ∀y1,y2 ∈ R; x1>x2 C (x1=x2 e Y1>y2) ˅ (y1=y2 e x1>x2) D x1>x2 e Y1>y2 E operação impossível em C
No conjunto C não em possível fazer a comparação de maior ou menor a única comparação possível é de igualdade, portanto a operação Z1>Z2 é impossível em C
(Veja aula sobre números complexos)
5. Qual é o quinquagésimo temo da sucessão numérica 1, 4, 7, 10…?
A. 157 B 151 C 150 D 149 E 148
A sucessão 1, 4, 7, 10…é uma progressão aritmética de a1=1 e d=3 então o seu termo geral de acorda com a forma do temo geral da progressão altimétrica é
an=a1+(n-1)d
an=1+(n-1)3
an=1+3n-3
an=3n-2
como queremos o quinquagésimo temo da sucessão n=50 vamos substituir n por 50 assim teremos o quinquagésimo termo
an=3n-2
a50=3•50-2=150-2=148
resposta o quinquagésimo temo da sucessão é 148
(Aula sobre progressão aritmética)
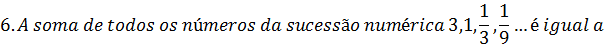
A. 4 B 4,5 C 4,75 D 5 E ∞
Estamos diante da soma de uma PG infinita com a1= 3 e r =1/3 a soma é dado pela formula;
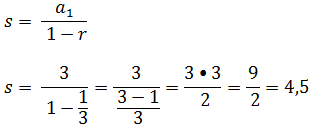
(aula sobre Progressão geométrica)
7. Da cidade A para a cidade B há m diferente caminhos. Para cidade B para a cidade C há n diferentes caminhos, qual é o numero de variantes Q existentes para viajar pelo itinerário A-B-C ? E qual é a probabilidade de um viajante escolher uma dessas variantes
A. Q=m+n, P=1/m+1/n B Q=m•n, P=1/m•n C Q=0,5(m•n), P=0,5(m/n+n/m) D Q=2(m+n), P=2/m+2/n E Q=2mn, P=2mn/m+n
O número de variantes Q existentes para viajar pelo itinerário A-B-C é dado pelo produto de número de caminhos de A para B e de B para C, ou seja Q=m•n
A a probabilidade de um viajante escolher uma dessas variantes será;
P=#CF/#CP
O viajante só poderá viajar por um caminho (não tem como viajar por dois ou mais caminhos em simultâneo) #CF=1
O número de casos possíveis é o número total de caminhos que é #CP=Q=m•n
Logo a probabilidadeé
P=#CF/#CP
P=1/m•n
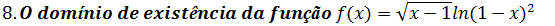
A. Dom=∅ B ]-1; 1] C ]1; ∞[ D Dom={1} E dom=R
Resolução
Para parte da raiz como não existe raiz de número negativo em Ir diremos
x-1≥0 e para parte do logaritmo (1-x)²>0
x≥1 e x\1
Então o Domínio é x>1 em forma de intervalo podemos escrever ; ]1; ∞[
(Veja aula sobre domínio de existência)
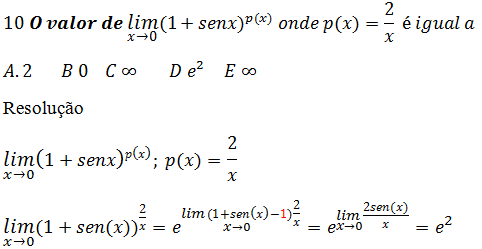
(Veja Como resolver limites exponenciais e limites trigonométricos)
11. A solução da inequação y1> y2 sendo y1 uma função não negative definida sobre a forma implícita satisfazendo a expressão x²+y1²-4=0 e y2=x , é o intervalo de variação da variável x a seguinte;
A. [-∞;∞] B [0; ∞] C [-2; 2] D [-2; √2] E ∅
y1 é uma semicircunferência de raio 2 (x²+y1²-4=0 → x²+y1²=2² ) e y2 é uma recta centrada na origem.
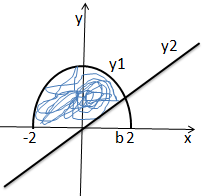
A partir desse gráfico podemos ver que a solução da inequação y1> y2 é de -2 atem b. Vamos calcular o valor de b, sento a a intercepção da semicircunferência e a recta.
x²+x²-4=0
2x² =4
x=±√2
o ponto b é x=2 (como é um ponto do lado positivo de x), lodo a solução da inequação y1> y2 é [-2; √2]

13. Qual é o período e o contradomínio Cf da função y=(sen(x)-cos(x))²
A T=2 π, Cf= [-1, 0] B T= π, Cf= [-1, 1] C T=2 π, Cf= [0, 1] D T=2π, Cf= [0, 2] E T=2π, Cf= [21, 0]
O período de função trigonométrica seno ou cosseno é 2π
A função y=(sen(x)-cos(x))² pode ser escrita como
y=(sen(x)-cos(x))²= sen²(x)- 2 sen(x) cos(x)+cos²(x)=1+ sen(2x)
vamos achar os valores máximos e mínimos da função y uma vem que -1≤sen(2x) ≤1
y=1+ sen(2x)
y=1+ (-1)=0
y=1+ 1=2
0≤y≤2
O contradomínio de f(x) é [0, 2]
14. Em que Dominio Df de variação do argumento x a função f(x)=x² admite a sua inversa f-¹(x), tal que os gráficos dessas funções interceptam-se em dois pontos ?
A. Df ; x ∈ ]- ∞; 0[ B Df ; x ∈ R C Df ; x ∈ [0; +∞[ D Df ; x ∈ ]- 1; 0[ E Não existe
f(x)=x² não e uma função invectiva logo não admite inversa
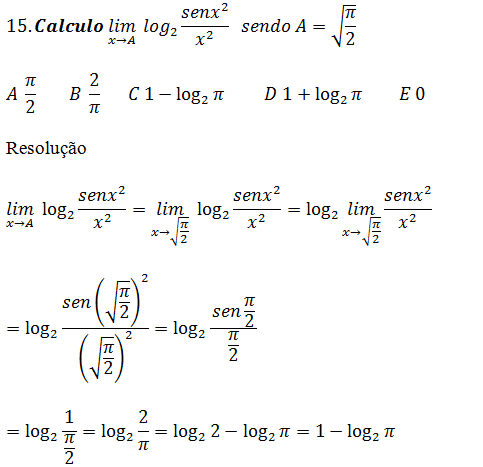
16. Qual é o valor da função A=f(2) para que seja continua a função f(x) definida de seguinte modo;

A. 4 B 0 C 2 D -2 E ∅
A função é continua se A=f(2) for igual ao limite
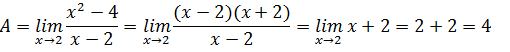
Resposta o valor de A=f(2) é 4
(Aula sobre continuidade de função)
17. Em que intervalo fica (m) o(s) zero(s) da função
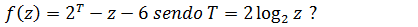
A [0;3[ B [1; 4] C ]-2; 0[ D [-2; 3] E ∅
Domínio
z>0
Agora vamos a equação
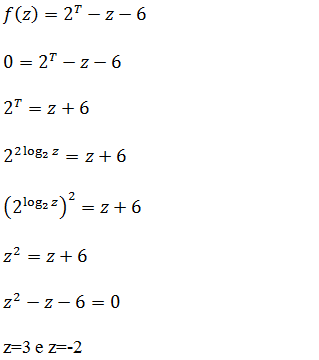
z=3 e z=-2
Como -2 não faz parte do domínio a solução é só 3 e 3 faz parte do intervalo [1,4]

A. ʎ ∈ [2; 3] B. ʎ ∈ ]1; +∞[ C. ʎ=2 D. ʎ ∈ ]- ∞; 1[ E ʎ ∈ [4;- ∞[
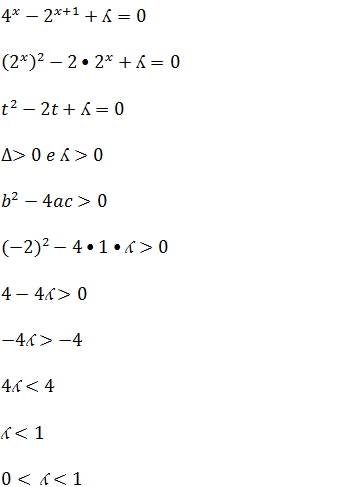

20. A solução da inequação |x|-x≤2 é ;
A. x ∈ [- 1; ∞ [ B Df ; x ∈ [-6;-4] C x ∈ [3; +∞[ D x ∈ [0; 4] E ∅
|x|-x≤2
|x|≤2+x
Df; 2+x>0
x>-2
Agora vamos resolver a equação
|x|≤2+x
x≤2+x ou x≥-2-x
x-x≤2 x+x≥-2
0≤2 2x≥-2
x≥-1
A solução é x≥-1 que representa-se por [-1, +∞[
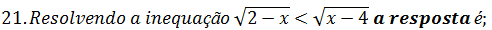
A. x ∈ ]2; 4 [ B Df ; x ∈ [2;4] C x ∈ [3; +∞[ D x ∈ [0; 4] E ∅
Primeiro vamos calcular o domínio
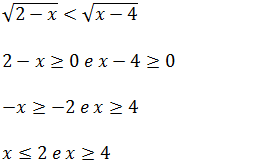
A partir do domínio podemos concluir que a a inequação não tem solução pois nenhum numero é menor que 2 e ao mesmo temo maior que 4

Olhando a gráfico notamos que os valores de t para qual a função f1(x)≥f2 (x) são t ∈ ]0; 1]
(Aprenda mais sobre logaritmos)
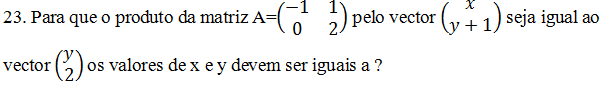
A. 4 e 0 B. 1 e 0 C. 0 e 4 D. 2 e 2 E. 3 e 1
Resolução
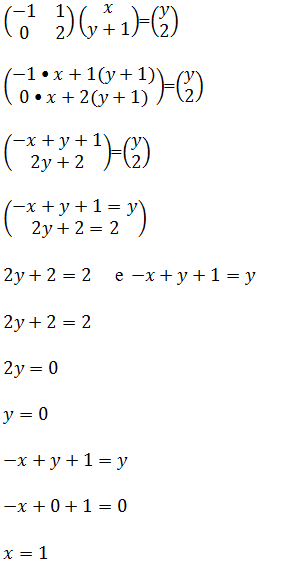
Resposta os valores de x e y devem são 1 e 2.
24.Considere o sistema Linear Segundo o paramento β, e a afirmação verdadeira é;
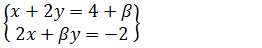
A. Se β =2 o sistema tem uma e só solução
B. Se β =2 o sistema não tem solução
C. Se β ≠2 e β ≠-2 o sistema tem mais do que uma solução
D. Se β ≠2 e β ≠-2 o sistema tem uma e só única solução
E. Se β =2 o sistema tem mais do que uma solução
Resolução
Vamos analisar o sistema Se β =2

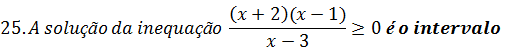
A. ∅ B ] -∞; 2 [ C ]1; 3[ D [-2; 1]U]3,+ ∞[ E ]- ∞; -2]U[1,3[
Vamos calcular os zeros de cada uma das expressões
x+2=0 →x=-2
x-1=0 →x=1
x-3=0 →x=3
a gora vamos construir a tabela
| x | -∞ | -2 | 1 | 3 | +∞ | ||||
| x+2 | – | + | + | + | |||||
| x-1 | – | – | + | + | |||||
| x-3 | – | – | – | + | |||||
| q | – | + | – | + |
Uma função é maior que zero onde for positivo então a solução da inequação será [-2,1]U]3, +∞ [ , (nota no três o intervalo é aberto porque 3 não faz parte do domínio)
(veja como resolver equações usando e método de tabela, método analítico)
26. As Assinptota Vertical Av, Horizontais AH, e oblíquas Ao, da função são

“Sempre” que existir Assinptota horizontal Assinptota oblíqua não existe como nesse exercício existe Assinptota horizontal Assinptota oblíqua não existe.
27. A curva cujo gráfico está representado na figura ao lado tem equação;
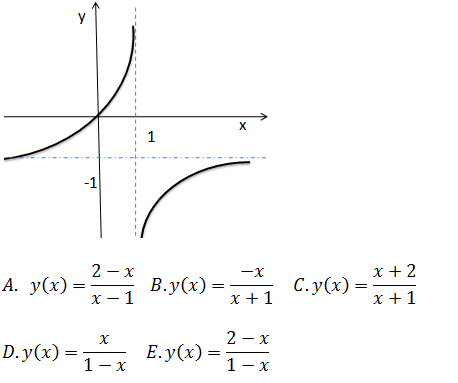
A ordenada a origem do gráfico é 0 então só pode ser alternativa B ou D
O domínio de existência do gráfico é x / 1 então a alternativa correcta é D.
28.As rectas no plano cartesiano y=½ x+5 e y=kx+b são perpendiculares quando
A. k=2, b=5 B. k=2, b=5 C. k=-2, b ∈ R D. k=1, b ∈ R E. k=0,5, b ∈ R
Duas rectas são perpendiculares se m1•m2=-1 (m1=½ e m2=k)
½ •k=-1
k=-2
As rectas no plano cartesiano y=½ x+5 e y=kx+b são perpendiculares quando k=-2 e b ∈ R
29.As abcissas dos pontos de infecção do gráfico da função
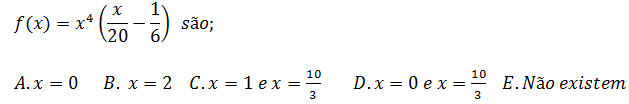
Vamos colar f(x) de uma forma que ira nos facilitar derivar
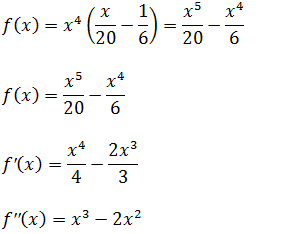
O ponto de infecção e um ponto em que a segunda derivada é igual a zero
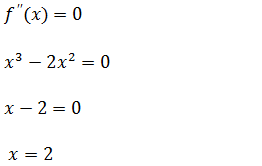
A abcissa do ponto de infecção é x=2
(Aplicação da primeira e segunda derivada)

Conteúdo relacionado:
- Manual de preparação para os exames de admissão
- Explicação para os exames de admissão
- Como fazer a inscrição para Up 2023
- Resolução de exames de admissão UEM
- Edital up 2023
Resultados dos exames de admissão ao Ensino Técnico Profissional 2026 já estão disponíveis
Os resultados dos exames de admissão ao Ensino Técnico Profissional (ETP) 2026 já estão disponíveis …
Resultados up 2026 (Já estão disponíveis)
Resultados dos Exames de Admissão da UP 2026 Os resultados dos exames de admissão à Universidade Ped…
Resolução de Exames de Matemática Admissão ISCISA 2019
Resolução de Exames de Matemática 2019 Admissão ao instituto superior de Ciências de saúde (ISCISA)&…
Resolução de exame de Matemática admissão a Academia Militar
Resolução de exame de Matemática 2018 admissão a Academia Militar 1. Considere o conjunto M = {x: x …
Resolução de Exames de Matemática Admissão UP 2018
1.Três camisas e cinco gravatas custam 4.600,00 Mt, duas camisas e três gravatascustam 3.000,00 Mt. …
Resolução de Exames de Química Admissão ISCISA 2019
1. Indique a alternativa FALSA: A. A água, o açúcar e o sal (dissolvidos) constituem um sistema mono…






