Calcular derivada usando logaritmização ajuda-nos a resolver derivadas que parecem difícil de calcular, a logaritmização simplifica o cálculo de algumas derivadas, usar logaritmização significa aplicar o logaritmo para simplificar a expressão e depois derivar aplicara regra da derivada de funções logaritmicas e outras propriedades da derivada com forme a necessidade de cada exercício
Exercícios Cálculo de derivada usando logaritmização

Essa função não existe uma regra imediata de calcular a sua derivada, vamos procurar uma maneira de simplificar ela usaremos a logaritmização.

Vamos aplicar logaritmo natural nos dois membros

De acordo com as propriedades de logaritmo o sen(x) pode deixar de ser potencia e passar a multiplicar o ln(x)

Agora vamos derivar os dois membros

Agora vamos isolar o y’ passa o y para multiplicar no sendo membro


Vamos derivar usando o mesmo procedimento do exercícios anterior logaritmização
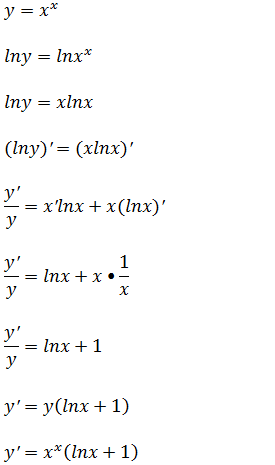


Para facilitar o cálculo dessa derivada vamos usar a logaritmização, usando a regra da derivada de funções irracionais teremos que depois usar a regra do quociente e usar a regra do produto duas vezes (uma vez para derivar o numerador e outra vez para, derivar o denominador) e ainda usar a derivada de funções exponenciais para deriva “e” elevado a x-2, e voltar a usar a regra de derivada de funções irracionais para derivar √(x²-2). Vamos enviar ter que fazer esses procedimentos usando a logaritmização.



Temos praticamente uma função composta por quatro funções derivar usando a regra da derivada do quociente será muito trabalhoso pois teremos que usar a própria regra do quociente e depois usara regra do produto por duas vezes, para evitar esse trabalho desnecessário vamos usar logaritmização para simplificar a
expressão

Exercícios para praticar: Calcule as derivadas das funções abaixo usando o método de logaritmização

