Limites indeterminações do tipo infinito sobre infinito

Limites contendo indeterminações do tipo infinito sobre infinito são limites em que ao substituir a variável pela sua tende temos uma “expressão” do tipo infinito sobre infinito.

Como resolver limites contendo indeterminações do tipo infinito sobre infinito?

Para resolver esse tipo de limites geralmente a aplica-se o mesmo método que a gente aplicou para resolver limites com indeterminações do tipo infinito menos infinito…

Cálculo de limites envolvendo indeterminações do tipo infinito sobre ínfimos

Exercício #1

Resolução do exercício #1 sobre limite

Primeiro vamos substituir onde vem x pela tendência que é infinito

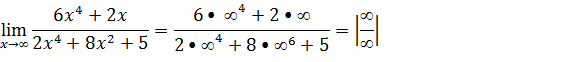
Temos uma indeterminação do tipo infinito menos infinito, para resolver este limites vamos evidenciar o termo de maior grão tanto no numerador assim como no denominador, no exercício em questão o termo de maior grão no numerador é o x⁴ e no denominador também é x⁴.

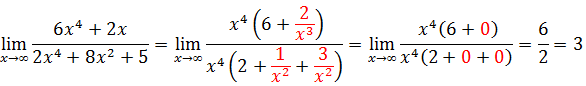
Poderá gostar de ver: Resolução de (Teste I) de Calculo I  

Exercício #2

Resolução exercício #2 sobre limite

Vamos substituir onde vem x pela tendência

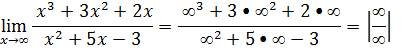
Assim como no primeiro exercício temos uma indeterminação do tipo infinito menos infinito, vamos aplicar o mesmo método para a resolução,  vamos evidenciar o termo de maior grão, no numerador é o x³ e denominador é x².

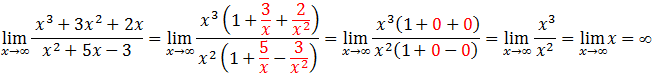
Exercício #3

Resolução exercício #3 sobre limite

Primeiro vamos substituir onde vem x pela tendência

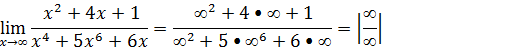
Vamos evidenciar o termo de maior grão tanto no numerador assim como no denominador,  no numerador é o x² e denominador é x⁴.

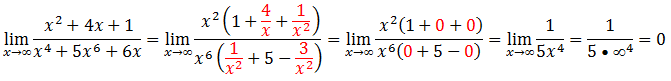
Exercício #4

Resolução exercício #3 sobre limite

Primeiro vamos substituir onde vem x pela tendência

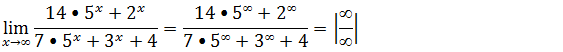
Para resolver este limites vamos evidenciar o termo de maior grão(a maior potencia )  tanto no numerador assim como no denominador,  no numerador a maior potencia é o 4˟ e no a maior potencia denominador é 5˟.

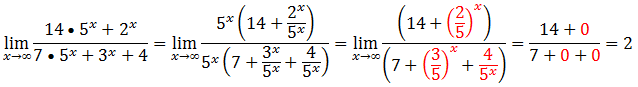
Exercício #5

Resolução do exercício #5  sobre limite

Primeiro vamos Substituir onde vem x pela tendência que é infinito (∞)

Para resolver este limites vamos evidenciar a maior potencia no numerador e no denominador, a maior potencia é o 4˟ no numerador e no denominador é 7˟.

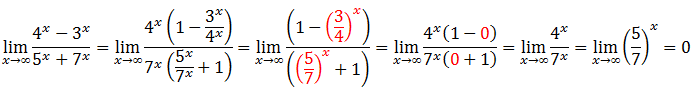
Exercício #6

Primeiro vamos substituir onde vem x pela tendência

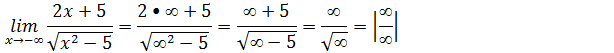
Tendo feito a substituição encontramos uma indeterminação do tipo ∞/∞ para resolver este limite vamos evidenciar a variável x no numerado por ser o temo de maior grão (no numerador) e no denominador vamos enviar o x² depois simplificar

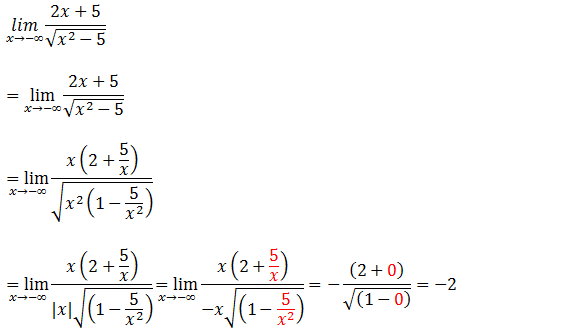
Exercício #7

Primeiro vamos Substituir onde vem x pela tendência que é infinito (∞)

Quando nós temos uma indeterminação do tipo infinito sobre infinito com expressões dentro da raiz vamos recorrer ao par conjugado.

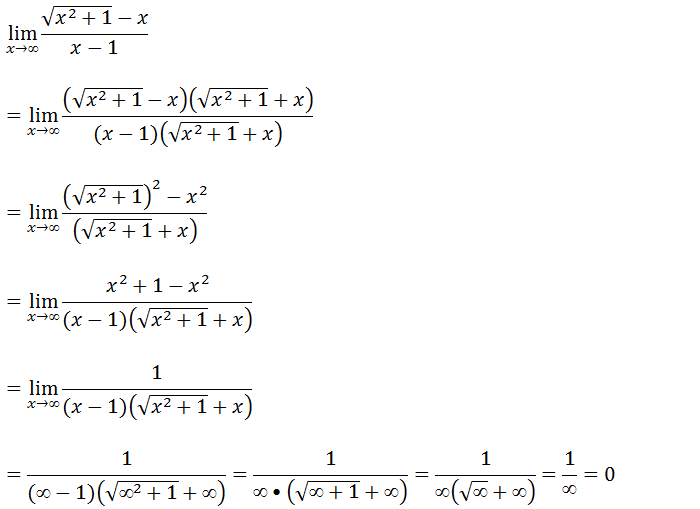
Exercícios de limites indeterminações infinito sobre infinito para praticar

Usamos os conhecimentos adquiridos a partir dessa aula e das aulas anteriores de calcule os seguintes limites:

Veja mais uma das nossa aulas

---