O que são Assimptotas ?
Assimptotas são rectas que o gráfico de uma determinada função tende a tocar e não toca.
Tipos de Assimptotas
Assimptota Oblíqua
A assimptotas Oblíqua (AO) é uma recta oblíqua que o gráfico tende a tocar mais não toca vejamos a assimptota oblíqua no gráfico abaixo;
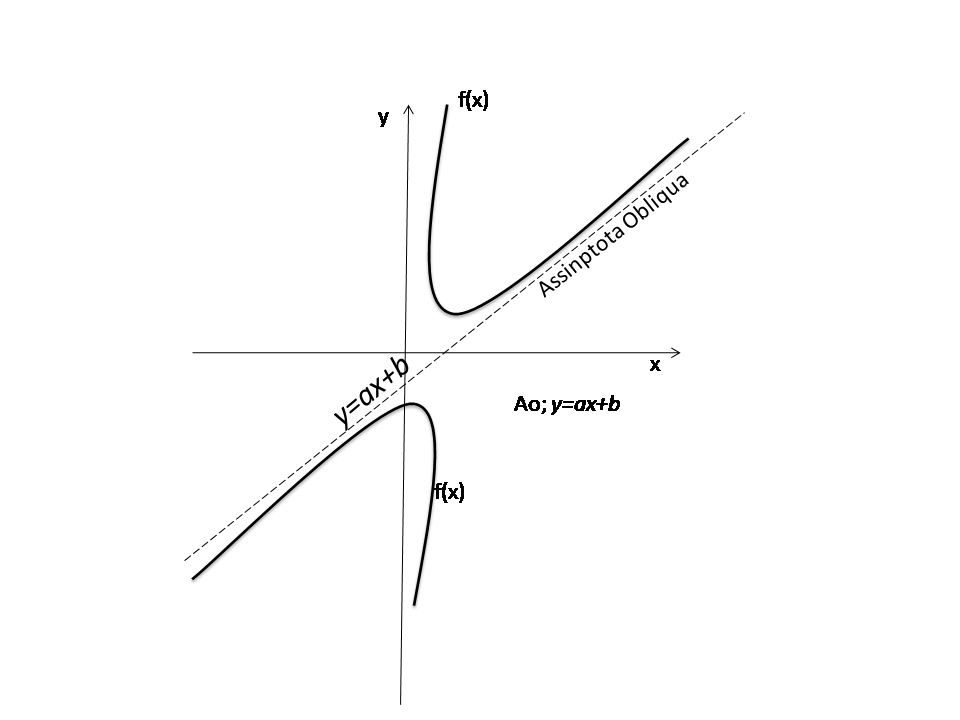
Como calcular / encontrar assimptota Obliqua?
Assimptota Obliqua é uma recta linear “y=ax+b” para encontrar essa recta basta apenas calcular os valores de a e b, que são calculados a partes das formulas;
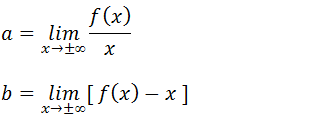
Encontrados esses valores de a e b temos assim a equação da assimptota Obliqua bastando substituir esses valores na formula da recta da assimptota Obliqua y=ax+b.
Assintota horizontal
A assimptotas horizontal (AH) é uma recta horizontal que o gráfico tende a tocar mais não toca vejamos a assimptota horizontal no gráfico abaixo;
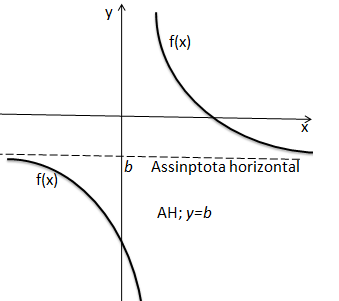
Como calcular / encontrar assimptota horizontal?
Assimptota horizontal (AH) é calculado a partir do limite da nossa função quando x se aproxima de infinito.
Assimptota Vertical
A assimptotas Vertical (AV) é uma recta vertical que o gráfico tende a tocar mais não toca vejamos a assimptota vertical no gráfico abaixo;
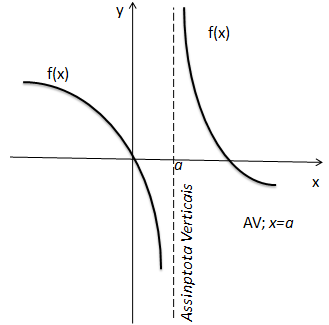
Como calcular / encontrar assimptota Vertical?
A assimptota Vertical (AV) é entrado a partir de uma análise, o limite da nossa função quando x se aproxima da assim vertical é infinito é essa base que usaremos basta encontrar o valor da Assimptota Verticais.
A Assintota Verticais é sempre um valor que não pertence ao domínio.
Resolução de exercícios de calculo de assinptotas
1.Encontre as assimptotas verticais, horizontal, obliquas para a função;
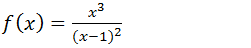
Resolução
Para Encontras as assimptotas verticais, horizontal, obliquas vamos usar as forma e o conhecimento teórico que aprendemos na explicação das assimptotas.
Assimptotas verticais
O valor provável da Assimptotas vertical é o valor que anula no denominador (que faz o denominador ser igual a zero)
Av; (x-1)²=0
x=1
Agora verificar se x=1 é uma Assimptota vertical calcando o limite da função quando x tende a 1.
Como o limite de f(x) quando x tende a 1 da infinito então x=1 é Assimptota vertical
AV; x=1
Assimptotas Horizontal
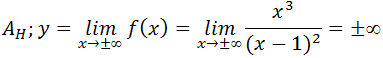
Assimptota Horizontal Não existe gráfico.
Assimptotas Obliqua
Já vimos que a assimptotas Obliqua é uma recta do tipo “y=ax+b” a partir das formulas que vimos quando estudamos sobre assimptotas Obliqua vamos calcular o valor de a e b
Primeiro vamos calcular o valor de ‘a”
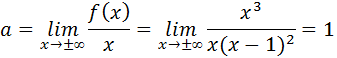
Agora vamos calcular o valor de “b”
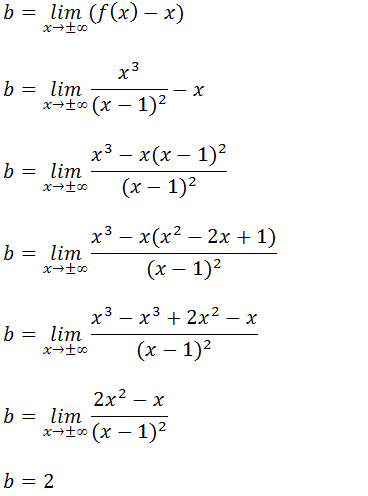

Com os cálculos que fizemos constatamos que para a função
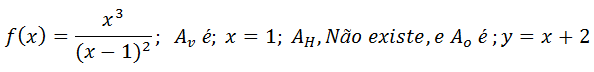
2.Encontre a assimptota vertical para a função;

O valor provável da Assimptotas vertical é o valo que anula no denominador (que faz o denominador ser igual a zero)
x-2=0
x=2
Agora verificar se x=2 é uma Assimptota vertical calculando o limite da função quando x tende a 2.
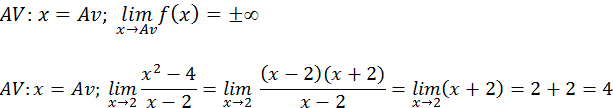
Como o limite de f(x) quando x tende a 2 não resultou em infinito então a recta x=2 não é Assimptota vertical(é apenas um ponto de descontinuidade e que não faz parte do domínio)
AV; Não existe nessa função
3.Encontre a assimptota vertical para a função;
O s valores prováveis da assimptotas verticais é o valor que anula no denominador (que faz o denominador ser igual a zero)
x²-9=0
x=±3
x=-3 ou x=3
Os valores prováveis da assimptotas verticais são x=3 e x=-3 devemos verificar se realmente são calculando limite da são quando “x” tende a esses valores se o limite for infinito é por que são.
**Como o limite de f(x) quando x tende a 3 não resultou em infinito então a recta x=3 não é Assimptota vertical.
**Como o limite de f(x) quando x tende a -3 resultou em infinito então a recta x=-3 é Assimptota vertical.
AV; x=-3
4.Encontre as assimptotas verticais, horizontal, obliquas para a função;
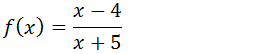
Assimptota verticais
O valor provável da Assimptota vertical é o valo que anula no denominador (que faz o denominador ser igual a zero)
x+5=0
x=-5
Agora verificar se x=-5 é uma assimptota vertical calculando o limite da função quando x tende a -5.
Como o limite de f(x) quando x tende a -5 da infinito então x=-5 é Assimptota vertical
AV; x=-5
Assimptota Horizontal
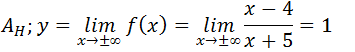
AH; y=1
Assimptota Oblíqua
Como nesse gráfico demos Assimptota Horizontal então assimptota Obliqua.
AO; Não existe.
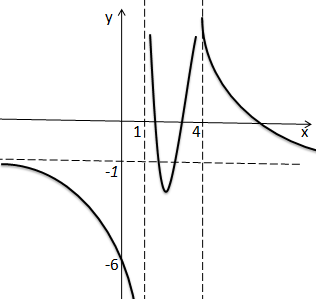
5. Indique as assimptotas, Vertical, Horizontal e Obliqua para o gráfico abaixo;
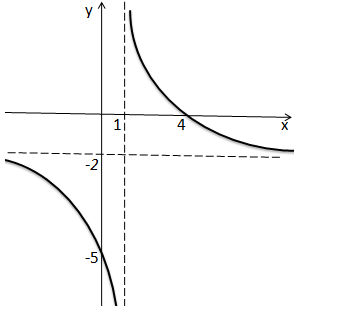
* A assimptotas Vertical é uma recta vertical que o gráfico tende a tocar mais não toca para o gráfico acima a recta é x=1
AV; x=1
* A assimptotas Horizontal é uma recta horizontal que o gráfico tende a tocar mais não toca para o gráfico acima a recta é y=-2
AH; y=-2
* A assimptotas Obliqua é uma recta Obliqua que o gráfico tende a tocar mais não toca, e no gráfico acima não existe nenhuma recta oblíqua que o gráfico tende a tocar e não toca logo não existe assimptota Obliqua.
Ao; Não existe, nesse gráfico
Exercícios para praticar calculo de assintotas
1.Encontre as assimptotas verticais, horizontal e obliquas para a função;
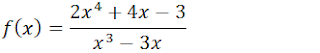
2.Encontre a assimptotas vertical horizontal e oblíquas, para a função;
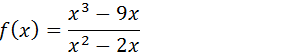
3.Encontre a assimptotas vertical para a função;
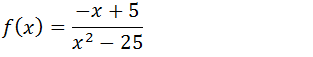
4.Encontre as assimptotas verticais, horizontal e obliquas para a função;
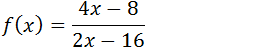
5. Indique as assimptotas, Vertical, Horizontal e Obliqua para o gráfico abaixo;