Derivada de uma função logarítmica
Nessa aula iremos aprender como derivar funções logarítmicas primeiro veremos como derivar funções logarítmicas.
Seja uma função logarítmica

Para achar a derivada função logaritmo vamos usar a definição de derivada usando limites
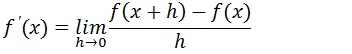
Substituindo pela nossa função, que é a função logaritmo para achar a derivada temos:
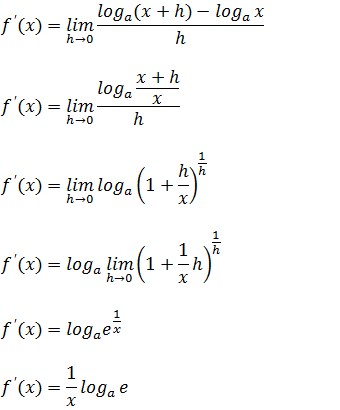
Vamos aplicar a propriedade de logaritmos de mudança de bases

Demonstração rápida e pratica de derivada de funções logaritmos
Uma forma muito rápida e de fazer a demonstração da derivada de funções logarítmicas é transformar a expressão logaritmo em uma expressão exponencial depois derivas ambos membros por fim isolar y derivada (y’)
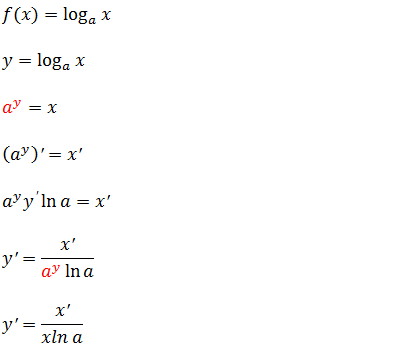
Derivada do logaritmo natural
Para derivar uma função logaritmo de com bane natural aplicamos a mesma forma que usamos para derivar uma função logaritmicas de base não natural a única diferença é que se a base for natural não precisamos de dividir por logaritmo natural da base, pois se a base for natural (a base for e) logaritmo natural da base vale um ( lne=1);
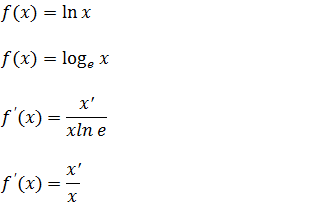
Exercícios de derivada de funções logarítmicas
a) Calcule a derivada da função ; f(x)=ln(x²+3x)
Vamos derivar essa função logarítmica aplicando longo a forma de derivada do logaritmo que é de derivar o logaritmo sobre o logaritmano sem derivar {f(x)=lnu f’(x)=u’/u }
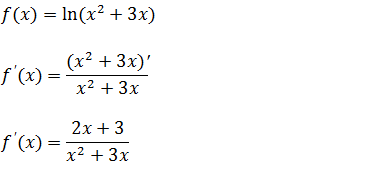
b) Calcule a derivada da função; g(x)=ln (4x³-x+2)
A derivada da função logaritmo g(x)=ln (4x³-x+2) será ada derivada de (4x³-x+2) sobre (4x³-x+2);
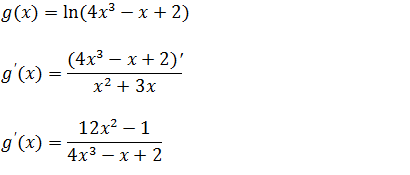
c) Calcule a derivada da função;y=ln(x+1)
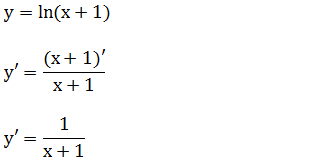
d) Calcule a derivada da função; f(x)=ln(2x⁵-3x²)⁴
Para simplificar a derivada dessa expressão logarítmica primeiro vamos tirar o expoente do logaritmano aplicando a propriedade do logaritmo[lnuⁿ=n•ln u]ou seja; ln(2x⁵-3x²)⁴= 4ln(2x⁵-3x²) dai temos uma constante a multiplicação uma função a derivada dessa função é só multiplicação a constante pela derivada da função.
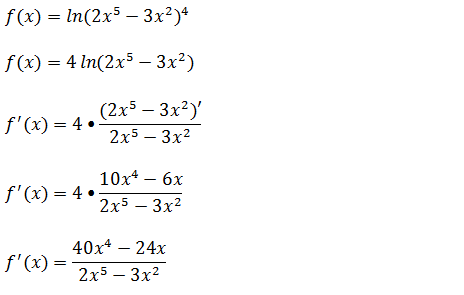
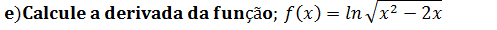
Para resolver essa derivada do logaritmo primeiro vamos transformar a raiz em potência e por conseguinte aplicar a propriedade de a potência multiplicação o logaritmo, depois derivar
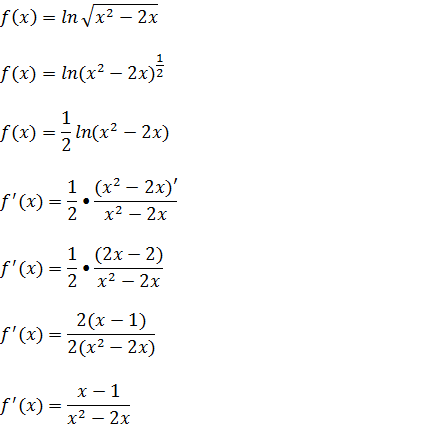

Derivar essa função logaritmo assim como esta pode nos dar muito trabalho desnecessário, para fazer a derivação dessa função vamos separa o logaritmo em duas partes que será o logaritmo do numerador menos o logaritmo do denominador depois derivar cada uma das parte assim teremos a derivada dessa expressão logarítmica.
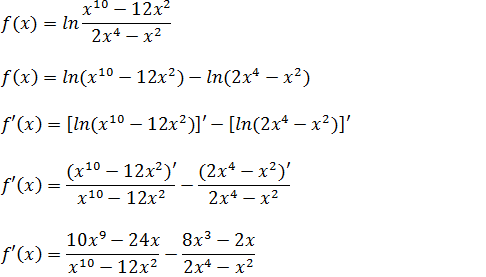
Exercícios para praticar derivadas de funções logarítmicas
Usado o conhecimento de derivadas de função logarítmica derive as funções abaixo; aplicando a formula de derivada de funções logarítmicas calcule;
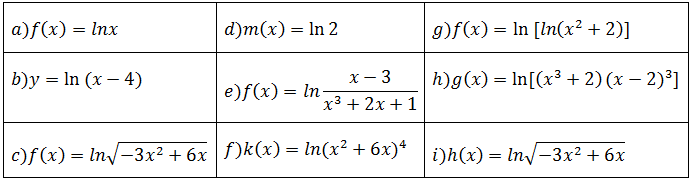
Assintota (Assintota horizontal, Assintota Vertical e Assintota Oblíqua)
O que são Assintotas? Assintotas são rectas que o gráfico de uma determinada função tende …
Derivada da função arctan(x) e arcctg(x)
Derivada de Funções Trigonométricas Inversas: Arctangente e Arcocotangente Após estudarmos as deriva…
Derivada de funções trigonométricas inversas y=arcsen(x) e y=arccos(x)
Dando início ao estudo das derivadas de funções trigonométricas inversas, começaremos pelas funções …
Derivada da função tangente e co-tangente
Nesta aula, aprenderemos a derivar as funções tangente e co-tangente. Para isso, utilizaremos exercí…
Derivada de funções trigonométricas (derivada de senx e cosx)
Derivada da função senx e cosx Nessa aula aprenderemos a derivar as funções trigonométricas do …
Derivada do quociente de função (Regra do quociente)
Derivada do quociente Para acharmos a derivada de y (derivada do quociente de u e v) Vamos…





