Derivada da função senx e cosx
Nessa aula aprenderemos a derivar as funções trigonométricas do tipo seno e a função cosseno.
Derivada da função senx
Para achar a derivada da função sen(x) vamos usar a definição de derivada usando limite.
Demonstração de derivada de senx
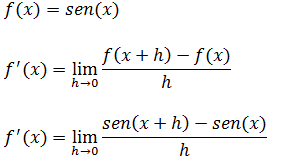
Seno da soma de dois ângulos é
sen(x+h)=sen(x)cos(h)+sen(h) cos(x)
Substituindo isso na nossa derivada temos
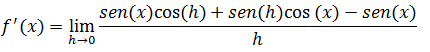
Vamos organizar a equação para podermos evidenciar o senx
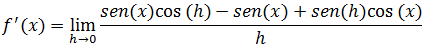
Vamos colocar o cosseno de x em evidência
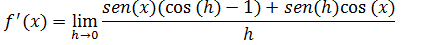
Vamos separar a fracção em duas fracções e tirar senx para fora do limite na primeira fracção na segunda tirar o cosx.
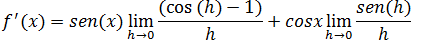
Na primeira fracção para podermos calcular o limite vamos multiplicar pelo par conjugado a na segunda vamos ter em conta que em um limite trigonométrico notável e da 1.
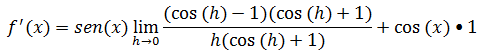
Recordando os casos notável
(com(h)-1)(com(h)+1)=cos²(h)-1²= cos²(h)-1=- sen²(h) e subistituindo isso no nosso mite temos;
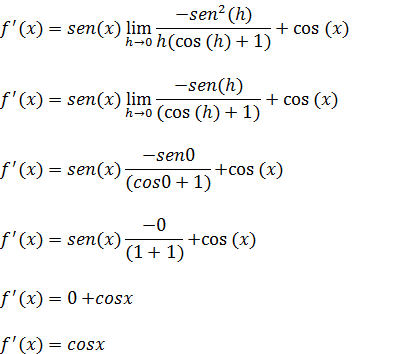
“A Derivada da função senx é a função cosx “
Derivada da função cosx
Tal como fizemos para achar a derivada da função senx iremos usar a definição de derivada para achar a derivada da função cosx
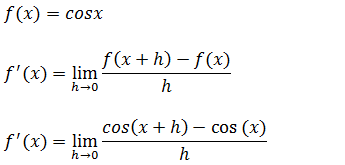
cosseno da soma de dois ângulos é
cos(x+h)=cos(x)cos(h)-sem(h)sen(x)
Substituindo isso na nossa derivada temos
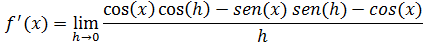
Vamos organizar a equação para podermos evidenciar o senx
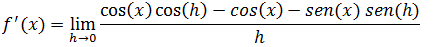
Vamos colocar o cosseno de x em evidência
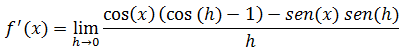
Vamos separar a fracção em duas fracções e tirar cosx para fora do limite na primeira fracção na segunda tirar o cosx.
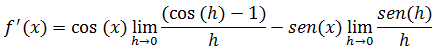
Na primeira fracção para podermos calcular o limite vamos multiplicar pelo par conjugado a na segunda vamos ter em conta que em um limite trigonométrico notável que da 1.
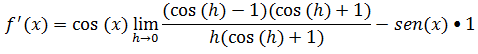
Recordando os casos notável
(com(h)–1)(com(h)+1)=cos² (h)–1²= cos² (h)–1=– sen² h e substituindo isso no nosso limite temos;
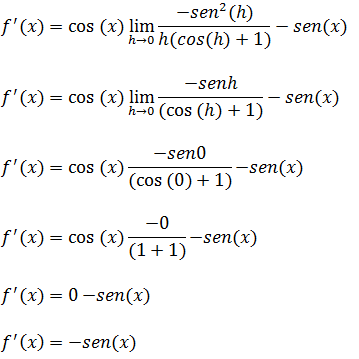
” A derivada da função cosx é a função –senx “
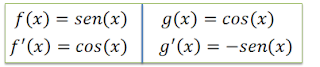 |
| Derivada de senx e cosx |
Derivada de funções trigonométricas compostas
Se tivermos uma função trigonométrica f(x)=sen (u) ou g(x)=cos (u) onde u é uma outra função qualquer que depende de x então ai estamos diante de uma função trigonométrica composta as derivas dessa função devem ser calculadas tendo em conta que são funções compostas, a derivada da função f(x)=sen(u) é a função f’(x)=u’cos(u) e a derivada da função g(x)=cos(u) é a função gʹ(x)=-u’sen(u);
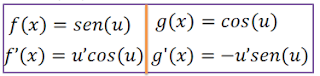
Forma alternativa de demonstrar a derivada da função y=cosx
Sabendo a derivada de funções trigonométricas podemos derivar a função cosseno conhecendo apenas a derivada da função senx, basta a penas transformai a função cosseno em função seno através da relação trigonométrica cosx=sen(90-x) dai como já conhecemos a derivada da função seno podemos derivar.
ƒ(x)=cosx=sen(90-x)
ƒ ‘(x)=(90-x)’cos(90-x)
ƒ ‘(x)=-cos(90-x)
ƒ ‘(x)=-senx
Exercícios sobre derivadas de funções trigonométricas
a) Calcule a derivada da função y=sen(x²-4x)
Estamos diante de uma função trigonométrica composta f(x)=sen(u) onde de acordo com o que vimos a sua derivada é f’(x)=u’cos(u) onde o nosso u vale x²-4x vamos usar esse conhecimento de derivada trigonométricas composta para derivar
y=sen(x²-4x)
yʹ=(x²-4x)ʹcos(x²-4x)
yʹ=(2x-4)cos(x²-4x)
b) Calcule a derivada da função y=sen(5x)
Para esse exercício y=sen(5x) de derivadas trigonométrica o nosso u vale 5x e vamos derivar usando a formula de derivada de funções trigonométricas y=sen(u) → yʹ=uʹcos(u) vamos ver a seguir a derivação;
y=sen(5x)
yʹ=(5x)ʹcos(5x)
yʹ=5cos(5x)
c) Calcule a derivada da função y=cos(2x³-1)
Usando a formula de derivada de funções trigonométricos y=cos(u) → yʹ=-uʹsen(u) temos;
y=cos(2x³-1)
yʹ=-(2x³-1)ʹsen(2x³-1)
yʹ=-(6x²-0)sen(2x³-1)
yʹ=-6x²sen(2x³-1)
d) Calcule a derivada da função y=sen(3x²+2x+7)³
Comparando com nossa forma y=cos(u) o nosso u vale (3x²+2x+7)³
então a derivada é yʹ=-uʹsen(u) seguiremos esse procedimento para derivar;
y=sen(3x²+2x+7)³
yʹ=[(3x²+2x+7)³]ʹcos(3x²+2x+7)³
yʹ=3(3x²+2x+7)² (3x²+2x+7)ʹcos(3x²+2x+7)³
yʹ=3(3x²+2x+7)² (6x+2)cos(3x²+2x+7)³
e) Calcule a derivada da função y=cos[e˟ (x+1)]
Para acharmos a derivada desse função não basta apenas saber a derivada da função trigonométrico é necessário também recordarmos da derivada do produto pois na nossa função temos um produto (no argumento).
y=cos[e˟ (x+1)]
yʹ=-[e˟ (x+1)]ʹsen[e˟ (x+1)]
yʹ=-[(e˟)ʹ (x+1)+ e˟ (x+1)ʹ]sen[e˟ (x+1)]
yʹ=-[e˟ (x+1)+ e˟ ]sen[e˟ (x+1)]
yʹ=-[e˟ (x+1+ 1) ]sen[e˟ (x+1)]
yʹ=-e˟ (x+2 )sen[e˟ (x+1)]
f) Encontre a derivada da função y=sen(cos(x))
A derivada dessa função trigonométrica será a derivada do argumento desse caso derivada da função cos(x) que multiplica cosseno do argumento nesse caso conforme já dissemos cos(x)
y=sen(cos(x))
yʹ=( cos(x))ʹcos(cós(x))
yʹ=-sen(x)cos(cosx)
g) Calcule a derivada da função y=sen(lnx)
Temos uma função trigonométrica onde o argumento é uma função logarítmicas e nos já aprendemos derivada de funções logarítmicas, então será fácil derivar derivada de funções
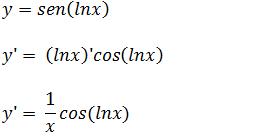

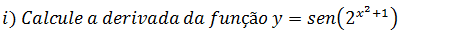
Nesse caso o argumento da função trigonométrica seno é uma função exponencial
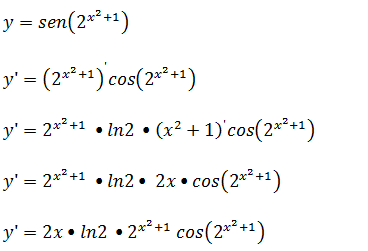
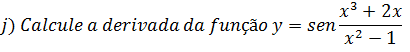
Para derivar essa função trigonométrica demos conhecer a derivada de um coeficiente pois temos um coeficiente no argumento.
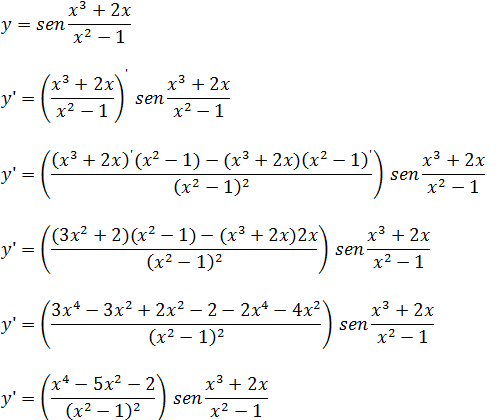
k) Calcule a derivada da função ƒ(x)=cos(e˟)
Com tudo que já aprendemos atem aqui essa função não nos dará nenhum trabalho para derivar
ƒ(x)=cos(e˟)
ƒ´(x)=- (e˟)ʹsen(e˟)
ƒ´(x)=- e˟sen(e˟)
l) Calcule a derivada da função ; ƒ(x)=(2x–1) sen(x³+2)
Estamos diante de um produto de duas funções então para derivar devemos usar a regra do produto.
ƒ(x)=(2x–1) sen(x³+2)
ƒ´(x)=(2x–1)ʹ sen(x³+2)+ (2x–1) [sen(x³+2)]ʹ
ƒ´(x)=2sen(x³+2)+ (2x–1) (x³+2)ʹcos(x³+2)
ƒ´(x)=2sen(x³+2)+ (2x–1) 3x²cos(x³+2)
ƒ´(x)=2sen(x³+2)+ (6x³–3x²) cos(x³+2)
m) Ache a derivada da função ƒ(x)= sen³(x²-3x)
Estamos diante de uma função composta do tipo y= uⁿ a sua derivada é yʹ= nuⁿ¯¹u’ onde a função a função trigonométrica sen³(x²-3x) é o nosso u , aplicaremos essa forma para derivar
ƒ(x)= sen³(x²-3x)
ƒ(x)=3 sen²(x²-3x)[ sen(x²-3x)]ʹ
ƒ(x)=3 sen²(x²-3x)[ (x²-3x)ʹ cos(x²-3x)]
ƒ(x)=3 sen²(x²-3x)[ (2x-3) cos(x²-3x)]
ƒ(x)=3 (2x-3) sen²(x²-3x) cos(x²-3x)
ƒ(x)=(6x-9) sen²(x²-3x) cos(x²-3x)
Exercícios para praticar derivadas de funções trigonométricas (derivada de senx e cosx)
Usado o conhecimento de derivadas de função trigonométricas seno e cosseno e outras funções aprendidas anteriormente derive as funções abaixo;
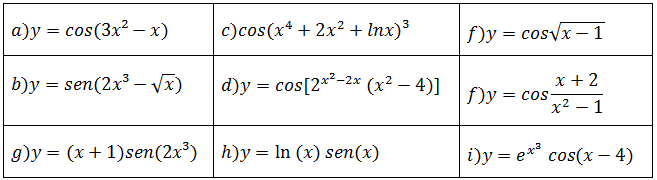
Assintota (Assintota horizontal, Assintota Vertical e Assintota Oblíqua)
O que são Assintotas? Assintotas são rectas que o gráfico de uma determinada função tende …
Derivada da função arctan(x) e arcctg(x)
Derivada de Funções Trigonométricas Inversas: Arctangente e Arcocotangente Após estudarmos as deriva…
Derivada de funções trigonométricas inversas y=arcsen(x) e y=arccos(x)
Dando início ao estudo das derivadas de funções trigonométricas inversas, começaremos pelas funções …
Derivada da função tangente e co-tangente
Nesta aula, aprenderemos a derivar as funções tangente e co-tangente. Para isso, utilizaremos exercí…
Derivada de funções trigonométricas (derivada de senx e cosx)
Derivada da função senx e cosx Nessa aula aprenderemos a derivar as funções trigonométricas do …
Derivada do quociente de função (Regra do quociente)
Derivada do quociente Para acharmos a derivada de y (derivada do quociente de u e v) Vamos…





