Derivada de uma expressão irracional simples
Vamos primeiro a achar a fórmula que nos permite derivar uma expressão irracional do tipo;

Vamos transformar a raiz em uma potência uma vez que nos ainda não sabemos derivar uma expressão com raiz;

Agora que já transformamos a raiz em potência , podemos já derivar aprendemos que a derivada de y=xⁿ é y’=nxⁿ¯¹ o nosso a para a expressão em questão é p/n, aplicando essa formula temos;
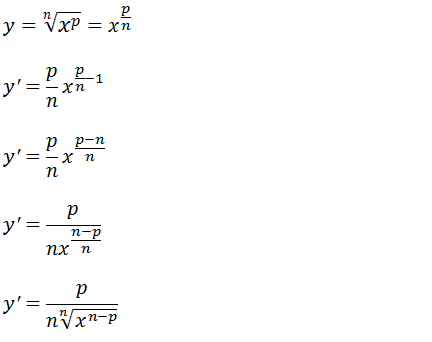
Demonstramos que ;

Calculo de derivas de funções irracionais simples
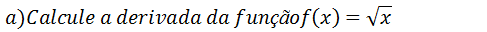
De acordo com a demonstração que fizemos para a derivada de funções irracionais temos;

Para a função do nosso exercício p=1 e n=2 (na raiz quadrada o índice é dois)vamos derivar aplicando essa formula

Vamos usar as formas de derivadas de funções com raiz tendo em conta que agora é uma raiz cúbica.
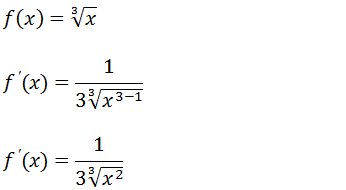
Derivada de uma função irracional composta

Acima vimos como derivar uma expressão que contem raiz e a expressão que esta dentro da raiz não é uma simples função (é uma função composta), agora vemos quando a expressão que esta dentro da raiz é uma expressão composta para isso vamos transformar a raiz em uma potência.
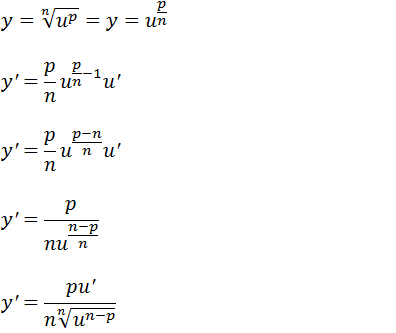
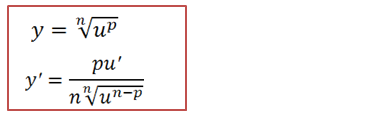 |
| Derivada de função irracionais composta |
Agora se for uma função u(x) de uma expressão que esta dentro de uma raiz quadrada

Tendo em conta que para uma função u dentro da raiz quadrada o índice da raiz é dois (n=2) e o expoente é um (p=1) temos;
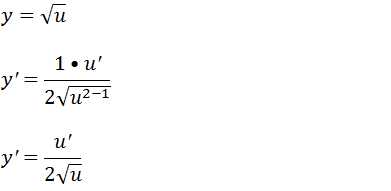
Calcule a derivada das seguintes funções irracionais
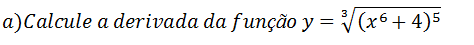
Para calcular a derivada dessa função irracional vamos usar a forma de derivadas de funções que contem raiz que fizemos a demonstração acima

Essa também é uma expressão irracional então sua derivada é obtida usando a mesma formula.
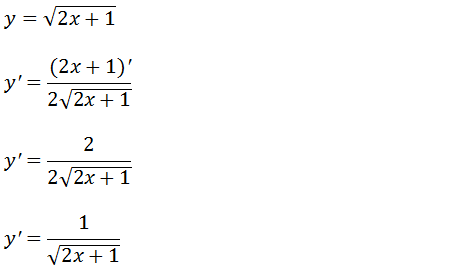

Para derivar essa função vamos seguir a mesma linha de raciocino de derivada de funções irracionais.

Podemos passar a raiz para o numerador mudando o sinal do expoente ta base para facilitar a derivação dessa função irracional;

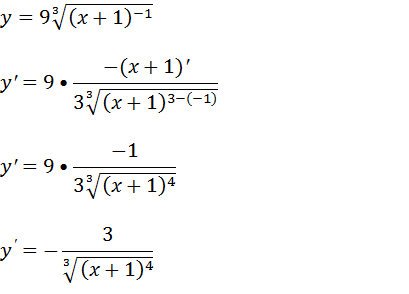
Exercícios para praticar derivadas de funções irracionais
Usado o conhecimento de derivadas de função irracional derive as funções abaixo aplicando a formula de derivada de funções irracionais;
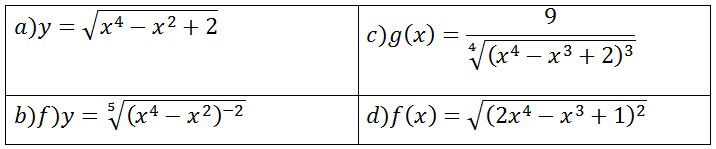
Assintota (Assintota horizontal, Assintota Vertical e Assintota Oblíqua)
O que são Assintotas? Assintotas são rectas que o gráfico de uma determinada função tende …
Derivada da função arctan(x) e arcctg(x)
Derivada de Funções Trigonométricas Inversas: Arctangente e Arcocotangente Após estudarmos as deriva…
Derivada de funções trigonométricas inversas y=arcsen(x) e y=arccos(x)
Dando início ao estudo das derivadas de funções trigonométricas inversas, começaremos pelas funções …
Derivada da função tangente e co-tangente
Nesta aula, aprenderemos a derivar as funções tangente e co-tangente. Para isso, utilizaremos exercí…
Derivada de funções trigonométricas (derivada de senx e cosx)
Derivada da função senx e cosx Nessa aula aprenderemos a derivar as funções trigonométricas do …
Derivada do quociente de função (Regra do quociente)
Derivada do quociente Para acharmos a derivada de y (derivada do quociente de u e v) Vamos…





