Acompanhe a resolução do Exame de Matemática 2020 Admissão a Universidade Pedagógica (Up), em caso de duvida com a resolução de alguma questão desse exame ou outro envie a sua duvida para nossa pagina do faceboock.

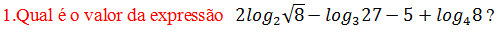
A. 2/7 B. -7/2 C . -2/7 D 7/2
Resolução da Q1 admissão UP 2020
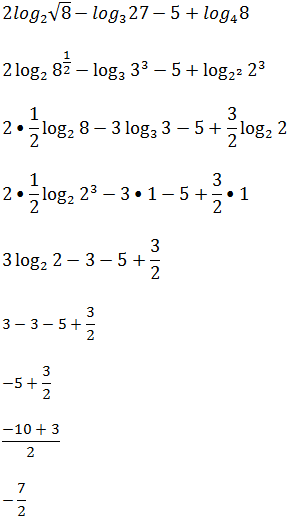
Resolução
3. Das três sentenças abaixo:
I sen 30′ = cos600 II √2+√3=√5 III{1,2}∈[1,2]
A somente a II é Verdadeira; B somente a III é falsa
C somente a III é verdadeira D somente a I é falsa
Demos conhecer a propriedade trigonométrica que diz
SenA=Cos(90°-A)
Vamos aplicar esse conhecimento
sen30°= cos (90°-30°)= cos60°
Então a alinha “A” é verdadeira sen 300= cos600 Verdadeira
A alinha “B” é falso √2+√3=√5 Falso
A alinha “C” é verdadeira {1,2}∈[1,2] Uma vez que no conjunto [1,2] os intervalo estão todos fechados significa que os números 1, 2 fazem parte do conjunto e o conjunto {1,2} pertence a um conjunto que cotem os números 1 e 2.
Resposta; A única afirmação falsa é alinha II
4.A razão entre a idade de Pedro e a de seu pai é igual a 2/9. Se a soma das duas idades é igual a 55 anos, então Pedro tem
A. 12 anos B.13 anos C. 10 anos D.15 anos
Representaremos a idade do Pedro por x e a idade do pai por y
A razão entre a idade de Pedro e a de seu pai é igual a 2/9 significa que x/y=2/9
a soma das duas idades é igual a 55 anos escrevemos matematicamente como x+y=55
Temos um sistemas de duas equações com duas incógnitas
{x/y=2/9
{x+y=55
Isolando x na primeira equação temos x=2y/9 substituindo essa expressão na segunda equação temos
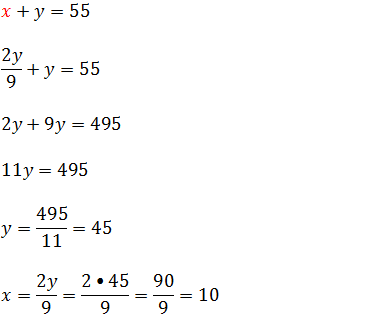
Representamos a idade do Pedro por x então o Pedro tem 10 anos
Resposta C

A.15/2 B.13/2 C.11/2 D.8/2
Resolução Q5 do exame de admissão Up
Estamos diante de uma fracção mista e para transformar a fracção mista em uma simples fracção demos o denominador da fracção e o numerador passa a ser o produto do numero que vem antes da fracção multiplicado pelo denominador, somado com numerador da fracção mista.
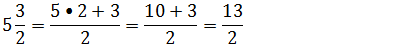
Resposta. B
6. Qual é a negação de Pᴧq
A. ~Pᴧq B. ~Pᴧ~q C. Pᴠ~q D. ~Pᴠ~q
Resolução Q6 do exame de admissão Up
A negação de Pᴧq é ~( Pᴧq)= ~Pᴠ~q
Resposta; D
7. Para construir a pipa representada na figura ao lado pelo quadrilátero ABCD, foram utilizadas duas varetas, linha e papel.
As varetas estão representadas pelos segmentos
AC e BD .A linha utilizada liga as extremidades A, B, C e D das varetas, e o papel reveste a área total da pipa.
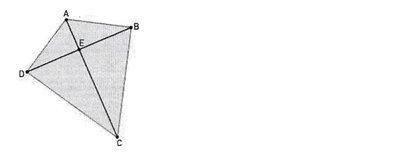
Os segmentos AC e BD são perpendiculares em E, e os ângulos ABC e ADC são rectos. Se os segmentos AE e EC medem, respectivamente, 18 cm e 32 cm, determine o comprimento total da linha, representada por AB + BC + CD+ DA.
A. 80cm B. l00cm C. 120cm D. l40cm
Resolução Q7 do exame de admissão Up
O quadrado da medida de AB é igual ao produto de AE e AC, e o quadrado da medida de BC é igual ao produto de EC e AC onde a partir da figura notamos claramente que AC=AE+EC=18+32=50cm
AB²=AE• AC=18•50→AC=30
BC²=CE• AC→BC=40
AB + BC + CD+ DA como AB=DA=30cm, BC=CD=40cm
AB + BC + CD+ DA=30cm+40cm +40cm +30cm=140cm
Resposta D

Vamos construir a tabela para resolver a inequação
| x | -∞ | 0 | 4 | +∞ | |||
| x-4 | – | 0 | – | 0 | + | ||
| 3x | – | 0 | + | 12 | + | ||
| q | + | ∅ | _ | 0 | + |
A equação é menor ou igual a zero onde não for positivo. ou seja solução é
X∈ ]0,4]
9.Sabe-se que o resto da divisão de um polinómio P(x) por binómio do tipo x-a é P(a). Qual é o resto da divisão de P(x) =5x3— 5x 2 + 5 por x+1
A. -1 B. 5 C. 1 D. -5
Resto é p(a) para temos o valor de a vamos igual a zero a expressão x+1
x+1=0
x=-1
a=x=-1
R=P(a)= 5•(-1)3— 5•(-1) 2 + 5=5•(-1)— 5•1 + 5=-5-5+5=-5
Resposta D
10.Na tabela abaixo, estão indicados os preços do rodízio de pizzas de um restaurante
| Dias da semana | Valor unitário do Rodízio(Mzn) |
| segunda-feira, terga-feira, Quarta-feira e quinta-feira | 277,5 |
| Sexta feira, sabado e domingo | 330 |
Considere um cliente que foi a esse restaurante todos os dias de uma mesma semana, pagando um rodízio em cada dia.
Determine o valor médio que esse cliente pagou, em reais, pelo rodízio nessa semana.
A.300 B.400 C.100 D.200
O clente foi ao restantate de segunda a domingo e de segunda a quita ele pagou 277,5 por dia entao nesse Cinco dias no total ele pagou 4•277,5Mt
E de sexta a domingo ele pagou 330Mt por dias nesses três dias no total ele pagou 3•330Mt
O Cliente no total pagou
Pt=4•277,5Mt +3•330Mt =2100,00Mt
A media será esse valor sobre o numero total de dia que são 7 (uma semana são 7 dias)
Md=2100,00Mt/7=300MT
Resposta A
11.A figura ao lado exibe o gráfico de uma função y =f(x) .
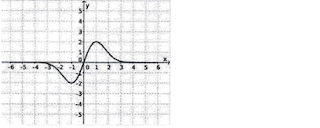
Então o gráfico de y=2f(x -1) é dado por
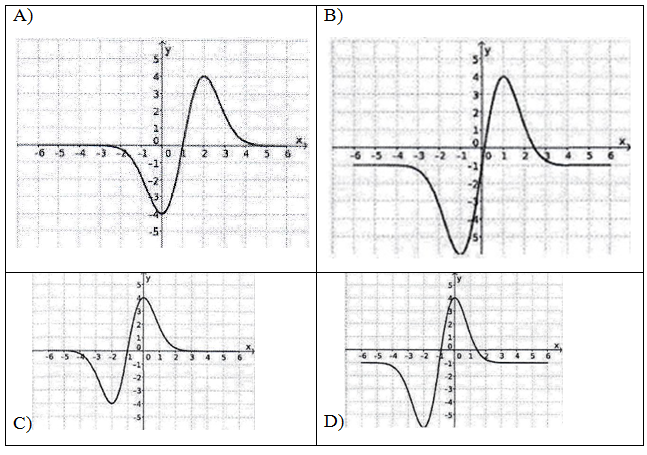
Primeiro na função f(x) vamos trasladar um unidade para direita
Depois vamos multiplicar a função por dois
Primeiro passo primeiro achar f¹=f(x-1)
f¹(2)= f(2-1)=f(1)=2
f¹(1)= f(1-1)=f(0)=0
a vamos vamos multiplicar por dois
y(2)=2 f¹(2)=2•2=4
y(2)=2 f¹(1)=2•0=0
A função onde temos os pontos y(2)=4 e y(0)=0 é alinha D
Resposta D
12.Considere um triângulo ABC, temos AC =3m, BC= 4m e B^=60°. Qual é o valor do sen(Å)
Primeiro vamos desenhar o triângulo com com os dados indicados
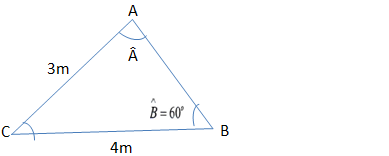
Vamos aplicar o teorema dos senos:
subistituindo os valores temos:
Note que:
O seno de o ângulo é sempre um valor menor ou igual a um como o valor encontrado é maior que 1, logo não existe um ângulo que o seno seja maior que 1. Logo a alternativa correcta é alinha D.
13. Para comprar os produtos A e B em uma loja, um cliente dispo e da quantia x, em meticais. O preço do produto A corresponde a 2/3 de x, e o do produto B corresponde a fracção restante. No momento de efectuar o pagamento, uma promoção reduziu em 10% o prego de A. Sabendo que, com o desconto, foram gastos 350,00Mts na compra dos produtos A e B, Qual é o valor, em meticais, que o cliente deixou de gastar.
A.25,00mt B.35,00mt C.45,00mt D.15,00mt
O preço
A=2x/3
B=(1-2x/3)
A=2x/3-0.1•2x/3=1.8x/3
A+B=350
1,8x/3+2x/3=350
2,8x/3=350
2,8x=3•350
2,8x=3•350
x=375
A=2x/3
A=2•375/3=250
O cliete deixou de gastar 10% do preco de A (o descont que ele teve)
Dp=10%A=0.1•250=25mt
Resposta A
14. Considere o gráfico da função. Para quais valores de x a função é crescente?
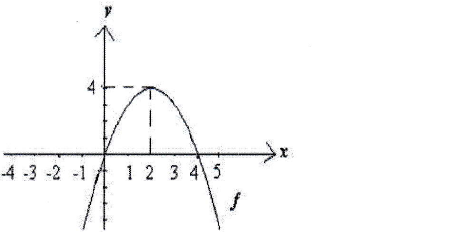
A. ]-∞ ; 0[ B. ]-∞ ; 2[ C. ]2 ; +∞[ D. ]4 ;+∞[
A função é crescente de ]-∞,2[
15. Sejam A:[0,8], B:[2,+∞[ e o Universo U=IR.Qual é o resultado da operação
A[-0; 2[ B. ]0 ; 2] C. ]0 ; 2 [ D. [0 ;2 ]
Vamos representar os conjuntos na recta real
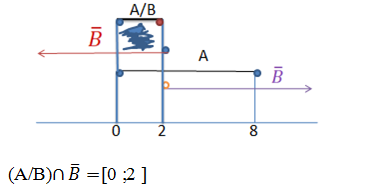
Resposta D
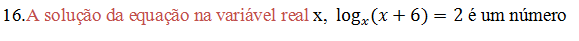
A. Primo B. Par C. Negativo D. Irracional

x+6=2˟
6=2˟-x
Para x=1
6=2¹-1=2-1=1
Para x=2
6=2²-2=4-2=2
Para x=3
6=2³-3=8-3=5
Para x=4
6=2⁴-4=16-4=12
A solução é um numero que esta no intervalo de ]3,4[ e nesse intervalo não tem números pares, primos, nem ímpar então a solução só pode ser um numero irracional
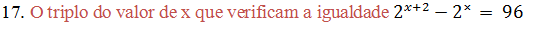
A.6 B.12 C.15 D.18

2˟•2²-2˟ = 96
2˟(2²-1) = 96
2˟(4-1) = 96
2˟•3= 96
2˟= 96 /3
2˟= 32
2˟= 2⁵
x=5
O triplo do valor de x é 3•5=15
Resposta C
18. Qual das seguintes expressões representam designação?
A. 3x- 4>2 B. 5x-2=9 C. 3 + 15 = 18 D.7-3•4
Na alinha “a” temos uma inequação, na alinha “B” uma equação na alinha “C” temos uma preposição NA alinha “D” é que temos uma designação.
Resposta D
19.Qual é a proposição verdadeira?
A.∀x ∈ IN : x²-5x = 0 C .∀x ∈ Z : x²- 5x =0
B ∄x ∈ IN : x²-5x = 0 D.∃x ∈ IN : x²-5x=0
Primeiro vamos resolver a equação
x²-5x=0
x(x-5)=0
x=0 ou x-5=0
x=5
Esses numeremos pertencem a ao conjunto IN e ão conjunto são apenas dois números não são todos então o quantificador que iremos usar e existencial ∃x ∈ IN : x²-5x=0
Resposta; D

A.]0;1[U]1;3[ B.]0,3[ C.]-3;3[ D.]- ∞;-3[U]3;+ ∞ [
9-x²>0
Vamos fazer o gráfico da função f(x)= 9-x²
9-x²=0
x²=9
x=±3

É maior que zero onde for positivo podemos ver no gráfico que é positivo no intervalo de ]-3;3[
Resposta; C