Trigonometria no triângulo rectângulo
Para estudamos e compreendermos as relações trigonométricas no triângulo, vamos desenhar a um triângulo.

O lado a chamaremos de cateto adjacente ao ângulo (x)
O lado b chamaremos de cateto oposto ao ângulo (x)
O lado c chamaremos de hipotenusa
Relações trigonométricas no triângulo rectângulo
- Seno do ângulo x representa a razão entre o cateto oposto (b) e a hipotenusa (c) ;

* Cosseno do ângulo x representa a razão entre o cateto adjacente (a) e a hipotenusa
(c) ;

- Tangente do ângulo x representa a razão entre o cateto oposto (b) e o cateto adjacente (a);

- Co-tangente do ângulo x representa a razão entre o cateto adjacente (a) e o cateto oposto (b);

Identidade trigonométrico fundamental
Demonstração de identidade trigonométrica fundamental
Visto que temos um triângulo rectângulo podemos escrever então é valido o teorema de Pitágoras
a²+b²=c²
Vamos dividir ambos membros por “c²”

No primeiro membro vamos colocar o numerador e denominador na mesma potencia, e no e no segundo membro temos pois c²/ c²=1.

Vimos que cos(x)=a/c e sen(x)=b/c então temos; cos²(x)+sen²(x)=1
Essa equação é chamado de identidade trigonométrico fundamental
cos²(x)+sen²(x)=1
A identidade trigonométrica tem muita aplicação em diverso ramos da matemática e não só.
Exercícios resolvidos sobre trigonometria no triângulo
1.Para a figura abaixo determine o valor de cos(x); sen(x) e tag(x)

A figura é um triangulo rectângulo e o lado x representa a hipotenusa portado pode ser calculado usando o teorema de Pitágoras.
Dados
b=3cm
a=4cm
Formula
cos(x)=c/a
O valor achar o valor de “c” usaremos o teorema de Pitágoras;
c²=a²+b²
c²=3²+4²
c²=9+16
c²=25
c=5
Agora tenho todos os valores do lado triângulo podemos facilmente calcular os valores desejada.
* cos(x) é a razão entre o cateto adjacente e a hipotenusa no nosso triângulo o cateto adjacente é “a” e a hipotenusa é “c”então cos(x) será;
cos(x)=a/c=4/5
- sen(x) é a razão entre o cateto oposto e a hipotenusa no nosso triângulo o cateto oposto é “b” e a hipotenusa é “c” então sen(x) será calculado como;
sen(x)=b/c=3/5
* tan(x) é a razão entre o cateto oposto e o cateto oposto no nosso exercício olhado o triângulo podemos ver que o cateto oposto é “b” e o cateto adjacente é “a” então tan(x) será encontrado a partir dessa razão;
tan(x)=b/a=3/4
Resposta; Os valores são; cos(x)=4/5 ;
sen(x)=3/5 ;tan(x)=3/4
2.Encontre os valores de h e b

Dados
h=?,b=?, c =6cm
A medida de h pode ser determinada recorrendo a função trigonométrica seno uma vez que temos a hipotenusa e o ângulo.

A medida de b (por se tratar do cateto adjacente) pode ser determinada recorrendo a função trigonométrica cosseno uma vez que temos a hipotenusa e o ângulo.

Observação; poderíamos também determinar a medida de b recorrendo ao teorema de Pitágoras.
3. Calcule a medida da altura do triângulo ADC de h

Vamos desenhar o triângulo com um ângulo oposto a altura que chamaremos de ß

Para o triângulo AEB tanβ corresponde a razão entre BE e AB;

Para o triângulo ADC tanβ corresponde a razão entre CD e AC;

O beta (β ) é o mesmo nas duas equações então vamos igualar as duas equações temos e calcular o valor da altura;

A medida de h é 10m
4.Calcule a altura da casa utilizando os conhecimentos de trigonometria

Dados
A altura da casa representa a media de AB, e este corresponde ao cateto oposto do triângulo ABC, e como temos o cateto adjacente e o ângulo podemos determinar a medida dessa altura usando a função tangente
h=AB=?
AC=4m
α =30˚

A altura da casa é de 4√3 m

já que temos a função seno para determinar o valor de cosseno podemos usar a identidade trigonométrica fundamental;

Exercícios sobre trigonometria no triângulo para praticar
1.Para a figura abaixo determine o valor de cos(x); sen(x) e tag(x)

2. Encontre os valores das medias da altura e da hipotenusa.

3.Sabendo que o valor de sen(x) é 0,8 entre o valor de cos(x)
4.Calcule a altura da casa utilizando os conhecimentos de trigonometria

5. Em um triângulo ABC sabe se que a medida de AB é 25cm e o ângulo  vale
30˚ determine a medida da altura desse triângulo.
Para terminar veja mais uma aula;
👉Teorema de Pitágoras (Resolução de exercícios e demonstração)
👉Tabela de ângulos especiais em grãos
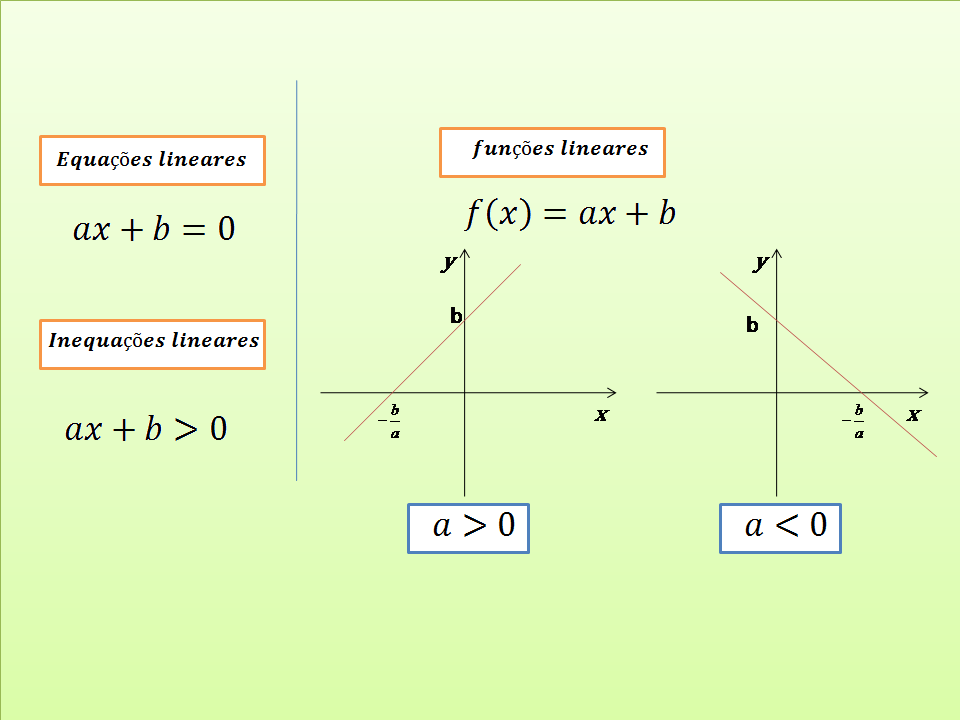
Equações lineares, Inequações lineares e funções lineares
O que são equações lineares Equações lineares são equações do tipo ax+b=0 com a≠0 Com…
Trigonometria tabela de ângulos especiais
Tabela de ângulos especiais em grãos Tabela de ângulos especiais em radiano Agora que já&…
Trigonometria no triângulo rectângulo ( Identidade trigonométrica fundamental )
Trigonometria no triângulo rectângulo Para estudamos e compreendermos as relações trigonométricas no…
Equação diferencial de Bernoulli
A equação diferencial de Bernoulli é Equação diferencial não linear que esta ou pode ser escrita na …
Cálculo de derivada usando logaritmização
Calcular derivada usando logaritmização ajuda-nos a resolver derivadas que parecem difícil de calcul…
Resolução de Exames de Matemática Admissão UP 2018
1.Três camisas e cinco gravatas custam 4.600,00 Mt, duas camisas e três gravatascustam 3.000,00 Mt. …