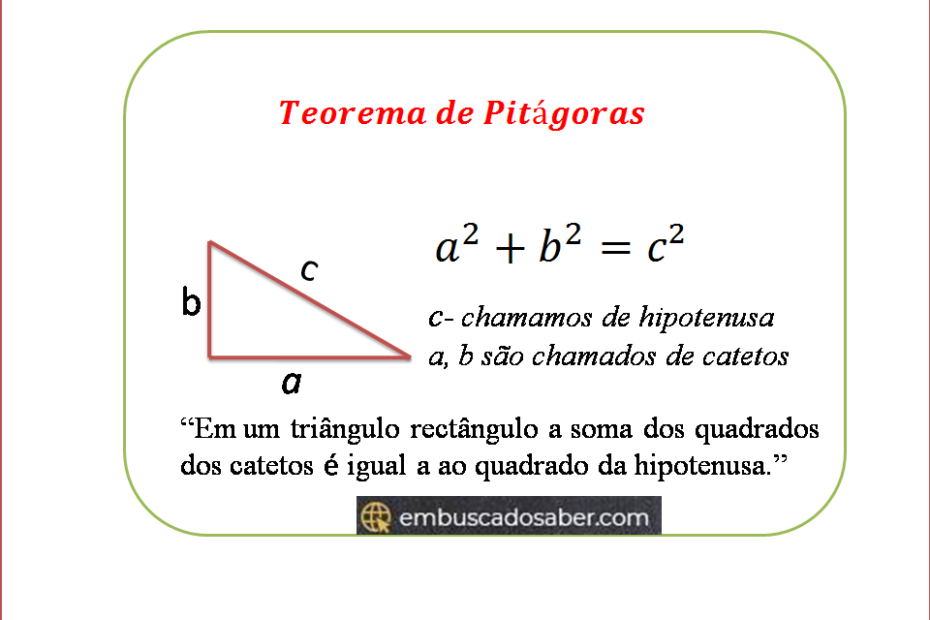
O teorema de Pitágoras ajuda-nos a resolver diversos exercícios de geométrica.
Enunciado do Pitágoras
Para um triângulo rectângulo a soma dos quadrados dos catetos é igual a ao quadrado da hipotenusa.
Demonstração teorema de Pitágoras
Para fazer a demonstração do teorema de Pitágoras, vamos desenhar um quadrado e dentro dele desenhar um outro quadro menor e inclinamos ele de modo que surjam 4 triângulos rectângulos idênticos
A área do quadrado é lado ao quadrado
* Para o quadrado externo o lado é (a+b) então a área do quadrado externo será Aex=(a+b)²
* Para o quadrado interno o lado é “c” então a área do quadrado externo será Ain=c²
“A área do quadrado externo é igual a soma da área dos 4 triângulos e do quadrado interno”
O que estamos a ver no triângulo é que;
c- chamamos de hipotenusa
a, b são chamados de catetos
O Teorema demonstrado acima é chamado de teorema de Pitágoras
Exercícios resolvidos sobre teorema de Pitágoras
1.Para a figura abaixo determine a mede do lado x
A figura é um triangulo rectângulo e o lado x representa a hipotenusa portado pode ser calculado usando o teorema de Pitágoras.
Dados
a=3cm
b=4cm
x=?
Formula
x²=a²+b²
Resolução
x²=3²+4²
x²=9+16
x²=25
x=√25
x=5
A medida do lado x do triângulo a vale 5cm
2.Calcule a mediada do cateto “y”
A figura é um triangulo rectângulo e sendo assim a lado y pode ser encontrado usando o teorema de Pitágoras, tendo em que a hipotenusa vale 25cm e um dos catetos vale 20cm e outro cateto é o y.
Dados
h=25cm
C1=20cm
y=?
Formula
h²=C²1+y²
Resolução
25²=20²+y²
625=400+ y²
y²=625-400
y²=225
y=√225
y=15
Feito os cálculos (recorrendo ao teorema de Pitágoras) constatamos que medida do lado y do triângulo a vale 15 cm
Trigonometria no triângulo rectângulo
3. Qual é a mediado do maior lado de um triângulo rectângulo os dois lados menores valem 12cm e 16cm.
O maior lado de um triângulo rectângulo é a hipotenusa, vamos desenhar um triângulo com as medidas dadas para facilitar a compressão
Dados
C2=16cm
C1=12cm
h=?
Formula
h²=C²1+ C²2
Resolução
h²=12²+16²
h²=144+256
h²=144+256
h²=400
h=√400
h=20 cm
A medida do maior lado do triângulo corresponde a medida da hipotenusa e feito os cálculos usando o teorema de Pitágoras podemos ver que a medida da hipotenusa (maior lodo do triângulo) vale 20 cm.
4.Calcule a altura da Maria
Dados
Observando a figura podemos notar que a altura da Maria representa um dos catetos do triângulo, portando pode ser determinado usando o teorema de Pitágoras.
Representaremos a altura da Maria como H, a hipotenusa como h (a partir da figura h=245) e o outro cateto como C1 (C1=147 de acordo com a figura).
h=245cm
C1=147cm
H=?
Formula
h²=C²1+H²
Resolução
245²=147²+H²
60025=21609+ H²
H²=60025-21609
H²=38416
H=√38416
H=196cm
A altura da Maria é de 1m e 96cm
5.Usando o teorema de Pitágoras, calcule a medida dos catetos de um triângulo rectângulo sabendo que a media de um dos catetos é dobro do outro e a hipotenusa vale 20 dm
Dados
C2=2C1
Resolução
h²=C²1+ C²2
20²= C²1+ (2 C1)²
400= C²1+4 C²1
400= 5 C²1
5 C²1=400
C²1=400/5
C²1=80
C1=√80
C1=√(16•5)
C1=4√5
Inicialmente dissemos que a medita do cateto dois é o doutro do cateto um, a partir dessa relação vamos determinar a medida do cateto dois.
C2=2C1
C2=2•4√5
C2=8√5
As medidas dos catetos são 4√5 dm e 8√5 dm.
6. Em um triângulo rectângulo ABC sabe se que a medida de AC é 6cm e AB é 8cm determine a medida do lado BC
Primeiramente vamos desenhar o triângulo rectângulo
A medida BC é a hipotenusa do triângulo rectângulo ABC, para a determinação (para o calculo da sua medida) usaremos o teorema de Pitágoras
Dados
AB=6cm
AC=8cm
BC=?
Formula
BC²=AB²+ AC²
Resolução
BC²=6²+8²
BC²=36+64
BC²=100
BC=√100
BC=10cm
A partir do teorema de Pitágoras podemos determinar o valor de BC e é 10cm
Exercícios sobre teoremas de Pitágoras para praticar
1.Para o triângulo abaixo determine a mede do lado y
2.Qual é a mediado do menor lado de um triângulo rectângulo sendo que os dois lados maiores a este medem 350cm e 256cm
3.Calcule a altura da casa utilizando o teorema de Pitágoras
4.Usando o teorema de Pitágoras calcule a medida do dos catetos de um triângulo rectângulo sabendo que a medida da hipotenusa é o triplo da medida de um dos catetos e o outro vale 5 cm.
5. Em um triângulo ABC sabe se que a medida de AB é 25cm e BC é 32cm determine a medida do lado AC sabendo que este é um triângulo rectângulo.