Nesta aula, aprenderemos a derivar as funções tangente e co-tangente. Para isso, utilizaremos exercícios práticos que nos ajudarão a entender o processo de derivação dessas funções trigonométricas.
Derivada da função tag(u)

Para achamos a derivada da função tangente vamos recordar que a função tangente é a razão entre a função seno e cosseno, uma vez que nos já aprendemos a derivar a função seno e cosseno já podemos derivar.
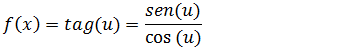
Agora que transformarmos tangente em um coeficiente da função seno e cosseno podemos derivar aplicando a regra da derivada do coeficiente.
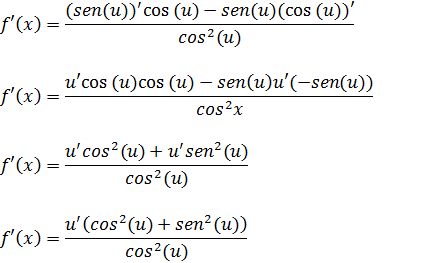
No numerador temos a identidade trigonométrico fundamental que da um.
cos²(u)+sen²(u)=1 iremos substituir cos²(u)+sen²(u) por 1 e então no numerador ficamos apenas com u’.

A Derivada da função y=tan(u) é y’=u’/ cos²(u)
Derivada da função ctg(u)

Seguindo o mesmo pensamento que o anterior vamos relembrar que a função tangente é a razão entre a função cosseno e seno.
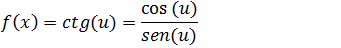
Vamos derivar aplicando a regra da derivada do coeficiente.
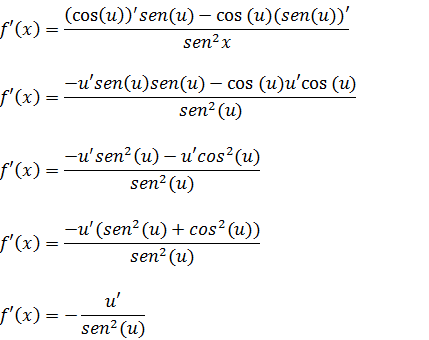
A Derivada da função y=ctg(u) é y’=-u’/ sen²(u)
| Derivada de função tag(u) e ctg(u) |
Derivada de função tag(x)
y=tag(x)
Para encontrar a deriva dessa função iremos usar a forma que nos demonstramos acima y=tag(u) → y’=u’/cos²(u) onde para o caso da função y=tag(x) o nosso u é o x
Derivada de função ctg(x)
y=ctg(x)
Para achar essa deriva iremos usar a forma que nos demonstramos acima y=ctg(u) → y’=-u’/ sen²(u) onde para o caso da função y=ctg(x) o nosso u é o x
y=ctg(x)
| Derivada de função tag(x) e ctg(x) |
Exercícios sobre derivada da função tangente e função co-tangente
a)Calcule a derivada da função y=tag(x³+3x)
Podemos resolver logo aplicando a formula y=tag(u) → y’=u’/ cos²(u);
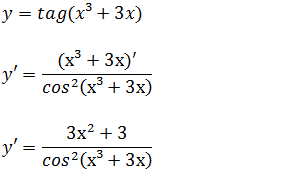
b)Calcule a derivada da função y=ctg(-x²+1)⁴
Para achamos a deriva da função y=ctg(-x²+1)⁴ vamos aplicar a forma da derivada função co-tangente y=ctg(u) → y’=-u’/ sen²(u) onde o nosso u é a função composta (-x²+1)⁴ iremos precisar de saber como derivar funções compostas.
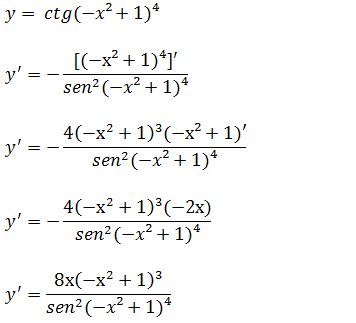
c)Calcule a derivada da função y=(x+2) tag(x)
Aqui temos um produto entre a função (x+1) e a função tag(x) para derivar devemos recorrer a regra do produto.
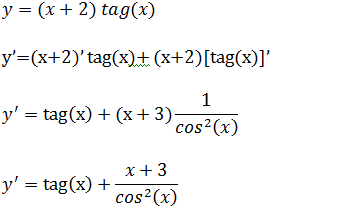
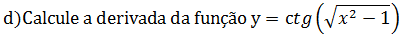
Vamos derivar aplicando a fórmula da derivada da função co-tangente, e iremos precisar saber a derivada da função irracional uma vez que temos uma raiz.
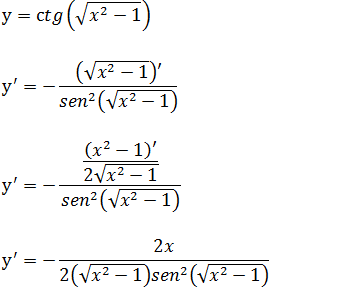

Vamos seguir a mesma metodologia para derivar, a formula de derivada de tangente y=tan(u) → y’=u’/ cos²(u) sendo que o nosso u para o exercício é [1/(x²-4)] .
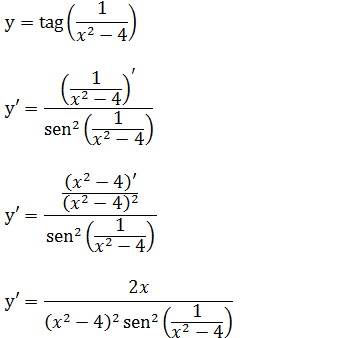

Temos um coeficiente entre a função ln(x) e a função tan(x) então para derivar vamos usar a regra do coeficiente.
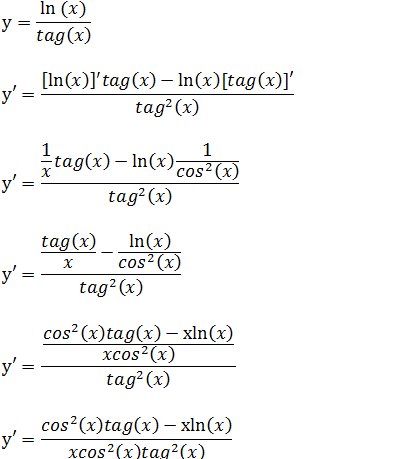
Podemos simplificar essa expressão uma vez que cos²(x) uma vez que tag(x)= cos(x)sen(x) e cos²(x) tag²(x)=sen²(x) substituindo isso na equação temos;
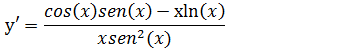
Exercícios para praticar derivadas de funções trigonométricas derivada de tag(u) e ctg(u)
Usado o conhecimento de derivadas de função trigonométricas co-tangente e tangente e outras funções aprendidas anteriormente derive as funções abaixo;
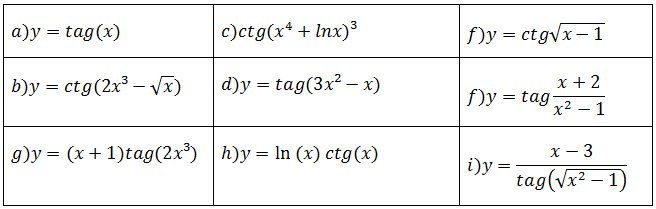
Assintota (Assintota horizontal, Assintota Vertical e Assintota Oblíqua)
O que são Assintotas? Assintotas são rectas que o gráfico de uma determinada função tende …
Derivada da função arctan(x) e arcctg(x)
Derivada de Funções Trigonométricas Inversas: Arctangente e Arcocotangente Após estudarmos as deriva…
Derivada de funções trigonométricas inversas y=arcsen(x) e y=arccos(x)
Dando início ao estudo das derivadas de funções trigonométricas inversas, começaremos pelas funções …
Derivada da função tangente e co-tangente
Nesta aula, aprenderemos a derivar as funções tangente e co-tangente. Para isso, utilizaremos exercí…
Derivada de funções trigonométricas (derivada de senx e cosx)
Derivada da função senx e cosx Nessa aula aprenderemos a derivar as funções trigonométricas do …
Derivada do quociente de função (Regra do quociente)
Derivada do quociente Para acharmos a derivada de y (derivada do quociente de u e v) Vamos…





