Regra L’Hospital para o calculo de limite
A regra de L’Hospital consiste em utilizar o conhecimento de derivadas para o cálculo de limites.
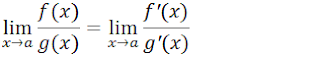
A regra de L’Hospital vem facilitar o cálculo de limites, a regra de L’Hospital simplifica o cálculo de diverso limites, porem a regra de L’lostital não se aplica para todo tipo de limites, mais a pesar disso é muito vantajosa usar regra de Hospital no cálculo de limites.
Quando é que podemos aplicar a regra de L’Hospital ?
Conforme a dissemos a regra de L’Hospital não se aplica para todo tipo de limites a regra de Hospital só se aplica para limites com indeterminações do tipo zero sobre zero ou infinito sobre ínfimo.
Exercícios resolvidos de cálculo de limite usando L’Hospital
1.Utilizando a técnica de L’Hospital (se possível) calcule
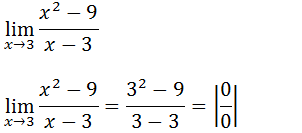
Como temos uma indeterminação do tipo zero sobre zero podemos usar a regra de L’Hospital
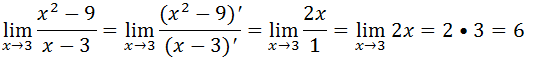
2. Recorrendo a regra de L’Hospital calcule o limite
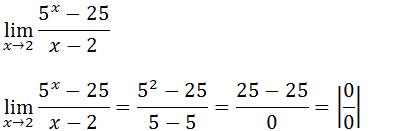
Como temos uma indeterminação do tipo zero sobre zero podemos usar a regra de L’Hospital
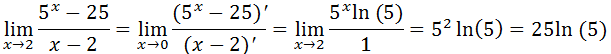
Veja como resolver esse limite sem usar a regra de L’Hospital (limite exponencial)
3. Calculo o limite
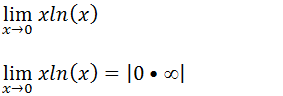
Não temos uma indeterminação do tipo zero sobre zero nem infinito sobre ínfimo então a função como se apresenta não podemos usar a regra de L’Hospital.
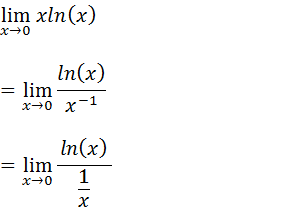
Agora temos uma indeterminação do tipo infinito sobre infinito já podemos usar a regra de L’Hospital Onde a função f(x)=ln(x) e a função g(x)=1/x vamos achar as suas derivadas
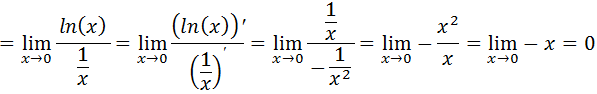
4.Calculo o limite usando a técnica necessária
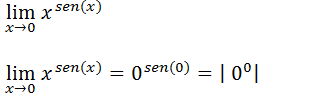
Temos uma indeterminação do tipo zero elevado a zero a zero não podemos usar a regra de L’Hospital pois a regra de L’Hospital so se aplica para indeterminação do tipo zero sobre zero ou infinito sobre ínfimo. Entao porá podemos usar a regra de L’Hospital vamos colocar a funcao de uma forma que tenhamos uma para indeterminação do tipo zero sobre zero ou infinito sobre ínfimo.
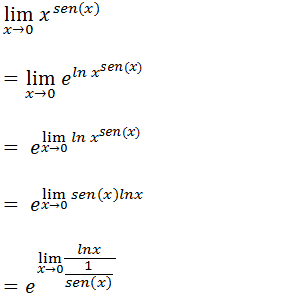
Agora temos uma indeterminação do tipo infinito sobre infinito já podemos usar a regra de L’Hospital Onde a função f(x)=ln(x) e a função g(x)=1/sen(x).
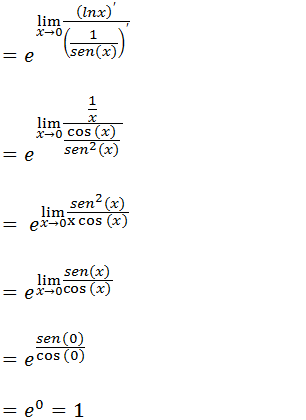
5.Usando a regra de H’lospital Calcule o limite a baixo
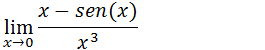
Vamos verificar o tipo de indeterminação
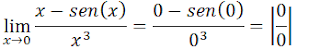
Como temos uma indeterminação do tipo zero sobre zero podemos usar a regra de L’Hospital
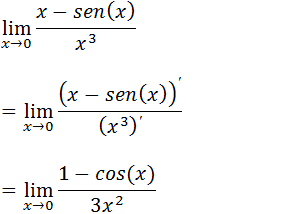
Ao Substituir pela tendência voltamos a ter uma indeterminação 0/0 então vamos Voltar a usar a regra de L’Hospital (derivar o numerados e denominar)
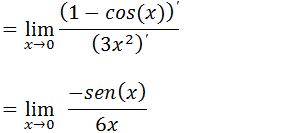
Ao Substituir pela tendência voltamos a ter uma indeterminação 0/0 então vamos Voltar a usar a regra de L’Hospital (derivar o numerados e denominar)
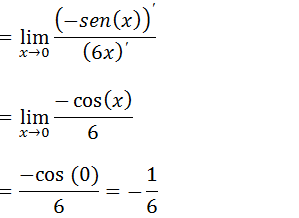
6.Calcule o limite utilizado derivadas
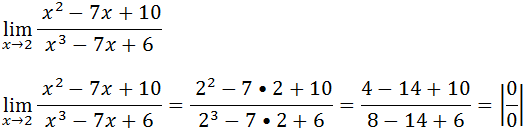
Como temos uma indeterminação do tipo zero sobre zero vamos usar a regra de L’Hospital
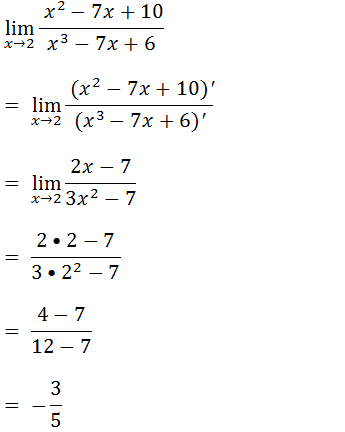
7.Calcule o limite recorrendo a derivada (regra de L’Hospital)
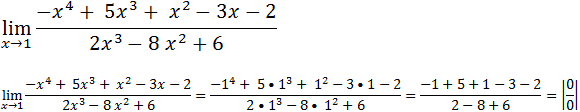
Como temos uma indeterminação do tipo zero sobre zero podemos usar a regra de L’Hospital
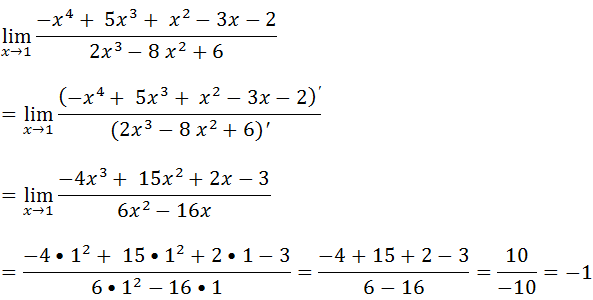
Veja outra forma de resolver sem usar a regra de L’Hospital
Exercícios para praticar limites usando L Hospital (usando derivada)
1.Utilizando a técnica de L’Hospital (se possível) calcule
2. Recorrendo a regra de L’Hospital calcule o limite
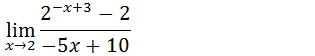
3. Calculo o limite
4.Calculo o limite usando a técnica necessária
5.Usando a regra de H’lospital Calcule o limite a baixo
6.Calcule o limite recorrendo a derivada (regra de L’Hospital)
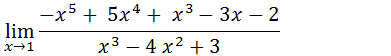
7. Calcule o limite de;
