Limite notável (limite exponencial)

O Limite notável é base para a resolução de diversos limites exponencial é praticamente impossível resolver limites exponenciais sem conhecer o limite notável.

Como resolver limites notável  contendo indeterminações do tipo zero sobre zero?

Limite notável

Demonstração

Primeiro vamos substituir o x pela tendência

Para calculamos este limite notável vamos fazer a substituição;

Vamos substituir no nosso limite

Limite notável com base Euler

Tenha sempre em mente os seguintes limites notáveis já demonstrados;

Exercícios resolvidos de aplicação de limites notável

Exercício #1 Limite notável

Primeiro vamos substituir o x por zero (que é tendência)

Para resolver esse limite vamos tirar o dois para fora do limite depois temos um limite notável.

Exercício #2 Limite notável

Vamos substituir o x pela tendência 

Esse é um limite notável vimos acima e já demonstramos.

Exercício #3 Limite notável

Primeiramente vamos substituir o x pela tendência 

Vamos dar um arranjar uma forma de termos um limite notável para isso vamos multiplicar por dois o limite e multiplicar por dois o denominador (multiplicar por dois e dividir por dois)

Exercício #4 Limite notável

Primeiro vamos substituir o x pela tendência

Vamos aplicar as propriedades de potência, vamos e separar o cinco elevado x mais cinco em duas potencias de base cinco e depois evidenciar o cinco elevado a três (que é cento e vinte cinco)

Exercício #5 Limite notável

Primeiro vamos substituir o x pela tendência 

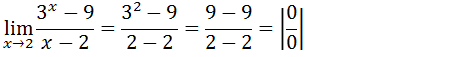
Vamos substituir x-2 por uma outra variável assim já teremos uma tendência para zero quem pode originar um limite notável

Aula em video

Exercícios de limites notável para praticar

Usamos os conhecimentos adquiridos nesta aula de limites notáveis juntamente com os conhecimentos básicos de matemática que tens calcule os seguintes limites:

Veja uma dessas aulas;