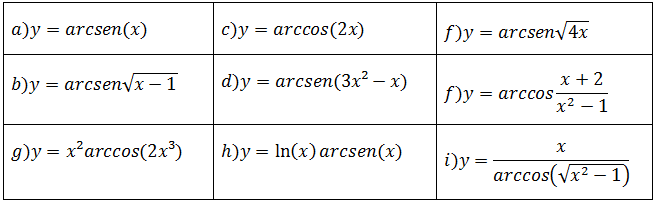Dando início ao estudo das derivadas de funções trigonométricas inversas, começaremos pelas funções inversas y=arcsen(x) e y=arccos(x).
Primeiramente, faremos a demonstração das fórmulas que utilizaremos para derivar essas funções. Em seguida, aplicaremos esse conhecimento na prática, resolvendo e explicando os exercícios abaixo.
Derivada da função inversa de seno (Derivada de função arcseno)
y=acsen(x)
Para calcular a Derivada da função y=arcsen(x) vamos colocar a função na forma x em função de y conforme sabemos se y=arcsen(x) então x=sen(y).
x=sen(y)
Tendo a função nessa forma já podemos derivar uma vez que conhecemos a derivada da função trigonométrica sen(y) e a derivada de x, então derivaremos ambos membros;
x’=(sen(y))’
x’=y’cos(x)
Vamos isolar a Derivada da função y (isolar y’) passando o cos(y) para dividir no outro membro

Vamos recorrer a identidade trigonométrica fundamental para calcular o valor de cos(y) em relação a x.
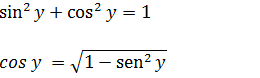
No segunda passa dessa demonstração dissemos que x=sen(y) então onde tem sem(y) iremos substituir por x
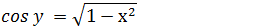
Então na expressão da Derivada da função inversa onde tem cos(y) iremos substituir por essa expressão e assim temos a derivada da função arcsenx
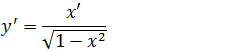
Derivada da função inversa de seno (Derivada de função arcseno)
y=arccos(x)
Para calcular a Derivada da função y=arccos(x) vamos colocar a função em na forma x(y) como fizemos para achara derivada da função arcseno .
x=cos(y)
Tendo a função nessa forma já podemos derivar uma vez que conhecemos a derivada da função trigonométrica cos(y) e a derivada de x, então derivaremos ambos membros;
x’=(cos(y))’
x’=–y’sen(y)
Vamos isolar y’ passando o sen(y) para dividir no outro membro
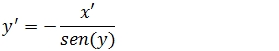
Vamos recorrer a identidade trigonométrica fundamental para calcular o valor de sen(y) em relação a x.
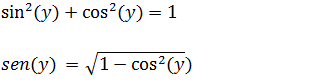
No segunda passa dessa demonstração dissemos que x=cos(y) então onde tem cos(y) iremos substituir por x
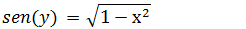
Então na expressão da Derivada da função inversa onde tem sen(y) iremos substituir por essa expressão e assim temos a derivada da função arccos(x)
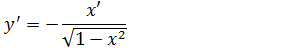
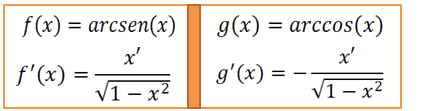
Exercício práticos derivadas de funções inversas arcseno e arccoseno
a)Calcule a derivada da função y=arcsen(3x)
Sabemos que se y=arcsen(u) então a sua derivada é y’=u’/√(1-u² ) vamos aplicar essa forma tendo em conta que para o nosso exercício o u é 3x.
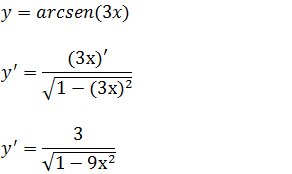
b)Calcule a derivada da função y=arccos(-x)
Se y=arccos(u) então a sua derivada é y’=-u’/√(1-u² ) vamos aplicar essa forma tendo em conta que para o nosso exercício o u é -x.
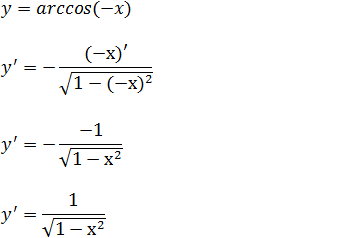
c)Calcule a derivada da função y=arccos(x²+1)
aplicando o mesmo procedimento que os das alinhas anteriores [ y=arcsen(u) então a sua derivada é y’=u’/√(1-u² ) ] temos;
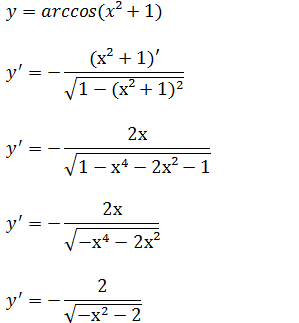
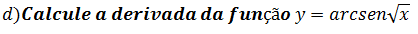
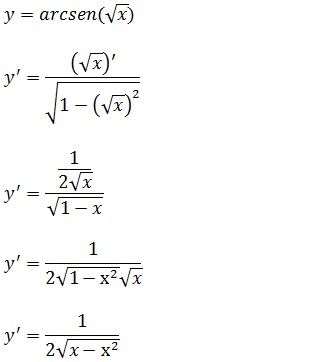
e)Calcule a derivada da função y=(x+2) arcsen(x)
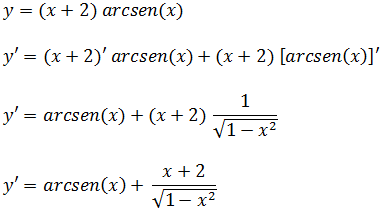
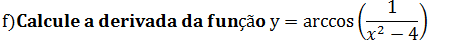
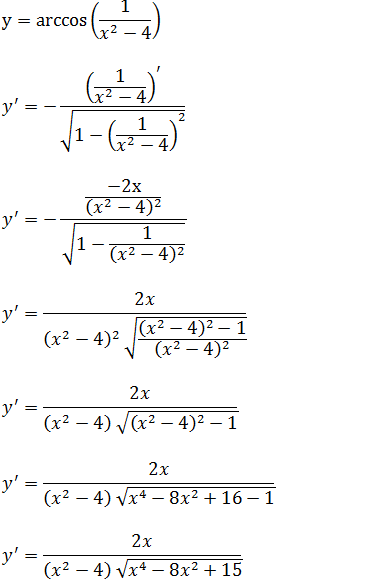
g)Calcule a derivada da função y=arcsen[ln(x)]
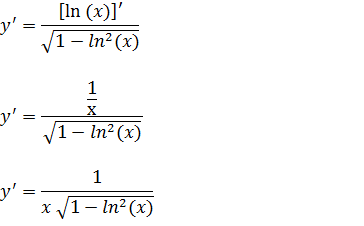
Derivada da função arcsen(x) e arccos(x) exercícios para praticar
Calcule a derivas das funções trigonométricas inversas abaixo;