Equações exponenciais são equações onde a variável esta no expoente. Ou seja são equações do tipo;
2x=1
5x+23x=2
Vale a pena recordar que se;
ac
a-> chamamos de base
c->chamamos de expoente. Exemplo:
23
2-> Chamamos de base
3->Chamamos de expoente.
Como fazer a leitura de potência:
ac
De forma geral (independentemente do expoente) podemos fazer a leitura da seguinte número. “a” elevado a “c” Exemplo de leituras de potência
| Potencias | Forma geral | Ou |
| 71 | Sente elevado a um | ——– |
| 72 | Sente elevado a dois | Sente ao quadrado |
| 73 | Sente elevado a três | Sente ao cubo |
| 74 | Sente elevado a quatro | Sente a quarta |
| 75 | Sente elevado a cinco | Sente a quita |
| … | … | …. |
Propriedades das potências
Pode também ver propriedades de logaritmos
Como resolver exercícios de equações exponenciais.
A principal base que nos devemos ter para resolução dos exercício;
ax=ay
x=y
Se nos tivermos as mesmas bases significa que os expoentes também são iguais.
Exercícios Ex1
a) 2x = 24
Como as bases são iguais os expoentes também devem ser iguais por isso dissemos x=4.
2x=24
x=4
Solução (4)
Ex2
b) 3x=27
Aqui nos temos bases diferentes vai em possível decompor o 27 e termos base 3 em ambos membros
Solução (3)
c) 125x-6-9=16
Que nos temos que reorganizar o exercício vamos passar o nove para o segundo membro e quando ele para o segundo membro fica positivo ou seja somamos nove e dezasseis que da vinte cinco e vinte cinco e cindo e vinte cinco podem ser decomposto em base cinco
No segundo para o terceiro passo não aplicamos a propriedade IV que esta indicada na tabela de propriedade de potencia.
Solução (7)
d)0.5*22x+1-5*2x=-4
Podemos aplicar a propriedade II e separar a parte do dois elevado a 2x+1 em em dois elevado a dois 2x vezes dois elevado a 1 conforme vimos na tabela de propriedades
0.5*22x+1-5*2x=-4
0.5*22x*2-5*2x=-4
Podemos simplificar um sobre dois com 0,5 dai temos:
22x-5*2x=-4
Não há nada que possamos que possamos fazer para que possamos ter a mesma base, e que temos como somar sem subtrair, mais olhando bem a nossa equação;
(2x)2-5*2x=-4
Podemos substituir dois elevado a x por uma outra variável
Seja; 2x=t
A equação fica
(t)2-5t=-4
Assim já temos uma equação quadrática bem simples vamos passar o quatro para o primeiro membro
t2-5t+4=0
Dai vamos calcular o valor de “t” (os zeros da função)
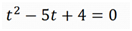
a=1; b=-5;c=4
∆=b²-4ac
∆=(-5)²-4×1×4
∆=25-16=9
t1=(5+3)/2 = 4
t2=(5-3)/2 = 1
Calculamos o valor de t mais o que nos queremos é calcular o valor de x vamos voltar na nossa condição onde dissemos que dois levados a x é igual a t e a partir dela calcular o valor de x.
Solução (0 ; 2)
Veja mais uma aula
Resultados dos exames de admissão ao Ensino Técnico Profissional 2026 já estão disponíveis
Os resultados dos exames de admissão ao Ensino Técnico Profissional (ETP) 2026 já estão disponíveis …
Resultados up 2026 (Já estão disponíveis)
Resultados dos Exames de Admissão da UP 2026 Os resultados dos exames de admissão à Universidade Ped…
Resultados UniLicungo 2026
Resultados dos exames de admissão a Universidade Licungo Os resultados dos exames de admissão à Univ…
Guia de Entrevista do Instituto de Formação de Professores (IFP)
📚 Guia Completo de Preparação para Entrevista do Instituto de Formação de Professores (IFP) Este liv…
Resultados dos Exames de Admissão ao IFP 2026
Os Resultados dos exames de admissão aos Institutos de Formação de Professores (IFP) para o ano lect…
Como consultar os resultados UP 2026
Como consultar os resultados dos exames de admissão a UP 2026 Os resultados dos exames de admissão a…





