Equações exponenciais são equações onde a variável esta no expoente. Ou seja são equações do tipo;
2x=1
5x+23x=2
Vale a pena recordar que se;
ac
a-> chamamos de base
c->chamamos de expoente. Exemplo:
23
2-> Chamamos de base
3->Chamamos de expoente.
Como fazer a leitura de potência:
ac
De forma geral (independentemente do expoente) podemos fazer a leitura da seguinte número. “a” elevado a “c” Exemplo de leituras de potência
| Potencias | Forma geral | Ou |
| 71 | Sente elevado a um | ——– |
| 72 | Sente elevado a dois | Sente ao quadrado |
| 73 | Sente elevado a três | Sente ao cubo |
| 74 | Sente elevado a quatro | Sente a quarta |
| 75 | Sente elevado a cinco | Sente a quita |
| … | … | …. |
Propriedades das potências

Pode também ver propriedades de logaritmos
Como resolver exercícios de equações exponenciais.
A principal base que nos devemos ter para resolução dos exercício;
ax=ay
x=y
Se nos tivermos as mesmas bases significa que os expoentes também são iguais.
Exercícios Ex1
a) 2x = 24
Como as bases são iguais os expoentes também devem ser iguais por isso dissemos x=4.
2x=24
x=4
Solução (4)
Ex2
b) 3x=27
Aqui nos temos bases diferentes vai em possível decompor o 27 e termos base 3 em ambos membros
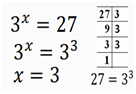
Solução (3)
c) 125x-6-9=16
Que nos temos que reorganizar o exercício vamos passar o nove para o segundo membro e quando ele para o segundo membro fica positivo ou seja somamos nove e dezasseis que da vinte cinco e vinte cinco e cindo e vinte cinco podem ser decomposto em base cinco
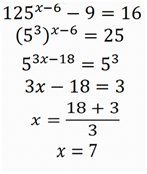
No segundo para o terceiro passo não aplicamos a propriedade IV que esta indicada na tabela de propriedade de potencia.
Solução (7)
d)0.5*22x+1-5*2x=-4
Podemos aplicar a propriedade II e separar a parte do dois elevado a 2x+1 em em dois elevado a dois 2x vezes dois elevado a 1 conforme vimos na tabela de propriedades
0.5*22x+1-5*2x=-4
0.5*22x*2-5*2x=-4
Podemos simplificar um sobre dois com 0,5 dai temos:
22x-5*2x=-4
Não há nada que possamos que possamos fazer para que possamos ter a mesma base, e que temos como somar sem subtrair, mais olhando bem a nossa equação;
(2x)2-5*2x=-4
Podemos substituir dois elevado a x por uma outra variável
Seja; 2x=t
A equação fica
(t)2-5t=-4
Assim já temos uma equação quadrática bem simples vamos passar o quatro para o primeiro membro
t2-5t+4=0
Dai vamos calcular o valor de “t” (os zeros da função)
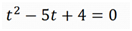
a=1; b=-5;c=4
∆=b²-4ac
∆=(-5)²-4×1×4
∆=25-16=9
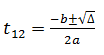
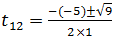
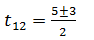
t1=(5+3)/2 = 4
t2=(5-3)/2 = 1
Calculamos o valor de t mais o que nos queremos é calcular o valor de x vamos voltar na nossa condição onde dissemos que dois levados a x é igual a t e a partir dela calcular o valor de x.
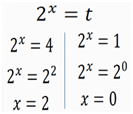
Solução (0 ; 2)
Veja mais uma aula
Resolução do exame de admissão ao ifp 2023
Acompanhe a resolução do exame de matemática admissão ao Instituto de formação de professores (IFP) …
Manual de preparação para exames de admissão de matemática ao IFP ano lectivo de 2024
Temos manual de preparação para exames de admissão de matemática ao IFP para o ano lectivo de 2024. …
Generalidades em equações paramétricas
Generalidades em equações paramétricas Podemos ter casos complexos em que o parâmetro se transforme …
Equações paramétricas
O que é uma Equações paramétricas ? Denomina-se por equação paramétrica a toda equação quadrática qu…
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Equações Lineares ou equação do 1º grau
Equação linear ou equação do 1º grau é toda a equação do tipo ax+b=0 onde: a é o coeficiente de x e…
Edital Acipol 2025
Informação sobre Edital de exames de admissão a academia de ciências policias (ACIPOL) para o ano le…
Resolução dos exames de Matemática de Admissão a Academia Militar 2024
Acompanhe a resolução do exame de Matemática 2024 admissão a Academia Militar no fim caso tenha inte…
Exames de admissão a academia militar de 2020 a 2024
Enunciado dos exames de admissão a academia militar dos anos 2020, 2021, 2022 , 2023 e 2024 em pdf B…
Edital de exames de Admissão Academia Militar 2025
Edital 2025 Academia Militar O edital de exames de admissão a Academia Militar para o ano lectivo de…
Bolsas de estudos para o Japão
1.bolsas de estudos para estudar no Japão O Instituto de Bolsas de Estudo, Instituto Público (IBE, I…
Bolsa de estudos para Itália 2024-2025
O Instituto de Bolsas de Estudo, Instituto Público (IBE, IP) tornou público que estão abertas candid…












