Resolução de Exames de Matemática 2019 Admissão ao instituto superior de Ciências de saúde (ISCISA) 

1. Qual da seguintes afirmações é verdadeira?

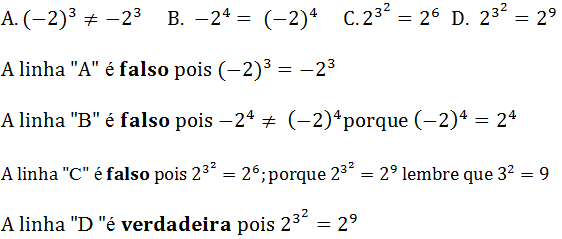
2.Numa pesquisa feita na cidade Maputo constatou-se que num universo de 100 jovens, 10 tem casa própria 8 tem casa própria e carro próprio, e 18 não tem casa própria nem caro próprio. Qual é o numero de jovem que tem somente carro próprio.

A. 72                  B.64         C. 68                     D. 66

Resolução

Vamos construir um diagrama

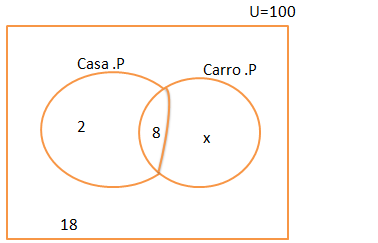
18+2+8+x=100

x=100-18-2-8

x=72

Resposta tem somente casa própria 72 jovens.

3.A Marília e a Nàira possuem juntas 2800,00Mt. A Marília tem 600,00Mt a mais do que a Nàira. A quantia da Marília é;

A. 2200                  B.1100         C. 1700                     D. 1900

Representemos a quantia da Marília por M e a quantia da Nàira Por N

A Marília e a Nàira possuem juntas 2800,00Mt ou seja M+N=2800

 A Marília tem 600,00Mt a mais do que a Nàira ou seja M=N+600

Temos um sistema de duas incógnitas vamos resolver;

M+N=2800

M=N+600

Na primeira equação vamos substituir M por N+600 e calcular o valo de N ( A quantia da Nàira para depois calcular a quantia da Marília)

N+600+N=2800

N+N=2800-600

2N=2200

N=1100

Tendo agora a quantia da Nàira vamos Calcular a quantia da Marília adicionado 600 (pois A Marília tem 600,00Mt a mais do que a Nàira )

M=N+600=1100+600=1700

R; A Marília tem 1700,00Mt

4. Observe a figura ao lado, qual é a medida de h ?

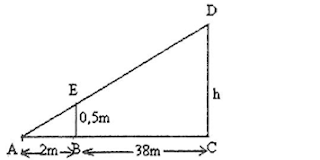
A. 20        B 10     C 30       D 5

Resolução

Vamos desenhar o triângulo com um ângulo ß

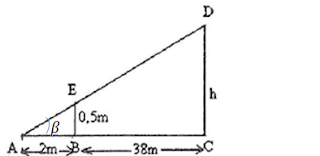
Para o triângulo AEB podemos dizer que;

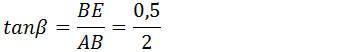
Para o triângulo ADC podemos dizer que;

Igualando as duas equações temos;

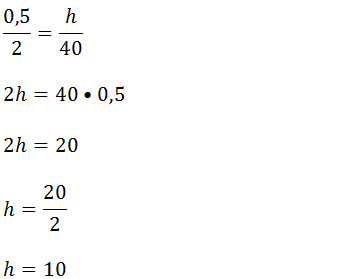
Resposta; a medida de h é 10m

7. As notas de 10 estudantes de uma turma de gestão hospitalar no exame de Estatística
aplicada são os seguintes; 12, 16, 20, 15. 19, 18,20,18, 15, 20. Os valores de B e D respectivamente, da tabela ao lado são;

A. 3 e 0,2       B. 3 e 0,3        C. 2 e 0,3            C. 2 e 0,2

Xi	12	15	16	18	19	20
fi	A	2	1	B	1	3
fri	0,1	C	0,1	0,2	0,1	D

 

B representa o
numero de vezes que a nota 18 se
repente então B de acordo com os dados a nota 18 se repente duas vezes B=2

D representa a Razão
entre o numero de vezes que a nota
20 se repente (que é 3) e o numero total de notas (que são 10)
então D=3/10=0,3

Resposta Os valores de B e D respectivamente são 2 e 0,3

8. As notas de 10 estudantes de uma turma de gestão hospitalar no exame de Estatística aplicada são os seguintes; 12, 16, 20, 15. 19, 18,20,18, 15, 20. O valor da mediana, da tabela ao lado é;

A. 18       B. 17        C. 16            C. 15

A mediana é o valor centrar (com dados organizados em ordem crescente)

Então para achar a mediana vamos organizar as notas depois indica o valor central (que é a mediana)

12, 15, 15, 16. 18, 18,19,20, 20, 20

Resposta: O valor da mediana é 18

 9.A soma dos elementos do conjunto solução da equação x⁴+3x²-4=0 é  

A. 5     B. 0     C. 4    D 1

x⁴+3x²-4=0

seja x²=t

t²+3t-4=0

t=-4 ou t=1

x²=t

x²=1

x=1 ou x=-1

a soma e 1+(=1)=0

Resposta: A soma dos elementos do conjunto solução da equação x⁴+3x²-4=0 é zero.

10. Considere a equação 3x²-(m+1)x+m-2=0 , qual é o valor de m de modo que a equação tenha raízes simétricas ?

A. m=2     B. m=-5     C. m=-1     D m=5

Uma equação quadrática tem raízes simétricas se b=0

E na equação b=-(m+1)

-(m+1)=0

-m-1=0

-m=1

m=-1

 Resposta o valor de m é -1

11. A figura representa os estudantes do ISCISA que frequentam o curso de Administração Hospitalar (AH), Tecnologia Biomédica (TB) e Saúde materna (SM). De acordo com afigura o número de estudantes que frequentam a Administração Hospitalar é de;

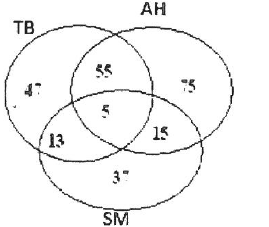
 A. 150         B.5       C.145        D. 60

Para achar o número de estudantes que frequentam a Administração Hospitalar vamos somar todos os estudantes que estão no “circulo” de Administração Hospitalar(AH)

#AH=55+5+15+75=60+90=150

Resposta: o número de estudantes que frequentam a Administração Hospitalar é de 150

12. A diferença (x-y) dos elementos do conjunto solução do seguinte sistema linear é;

{3x+y=1

{2x-3y=8

A  -1        B 1        C 3   D -3

Resolução

{3x+y=1

{2x-3y=8

Vamos multiplicar por três a primeira equação depois fazer adição ordenada
coma segunda equação;
{9x+3y=3

{2x-3y=8

————-

11x=11

x=11/11

x=1

Agora vamos achar o valor de y a partir da primeira equação substituindo x por 1

{3x+y=1

3•1+y=1

3+y=1

y=1-3

y=-2

logo:  x-y=1-(-2)=1+2=3

Resposta: A diferença (x-y) dos elementos do conjunto solução é 3

13. Observe a figura ao lado, a expressão analítica de f(x) é;

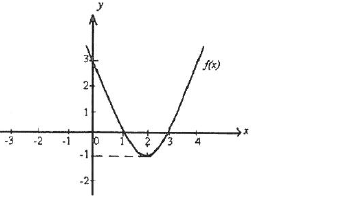
A f(x)=x²+4x+3         B
f(x)=x²+4x-3       C f(x)=x²-3x+4    D f(x)=x²-4x+3

Dados

X1=1

X2=3

Yv=-1

Xv=2

Podemos determinar a expressão analítica a partir de ;

Y= a (x-x1)(x-x2)

-1=a(2-1)(2-3)

-1= a •1•(-1)

-1= -a

a=1

Agora tendo o valo de a vamos voltar na nossa formula f(x) = a (x-x1)(x-x2) e substituir “a”pelo seus valor(a=1) e as raízes também pelo seus valores (x1=1, x2=3)

f(x)= 1 (x-1)(x-3)

f(x)=(x-1)(x-3)

f(x)=x²-3x-x+3

f(x)=x²-4x+3

A expressão analítica da função f(x) é f(x)=x²-4x+3

 14. O conjugo solução da inequação ½ x-4≥3x+1

A x ∈]-∞,-2]         B x ∈]-∞,2]         C x ∈]-∞,-2[        D x ∈]-∞,2[

Resolução

½ x-4≥3x+1

x-8≥6x+2

x-6x≥2+8

-5x≥10

5x≤-10

x≤-10/5

x≤-2

Em forma de intervalo podemos escrever ; x ∈]-∞,2] 

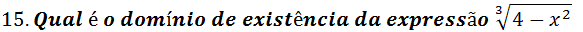
A x ≥±2            B x ≤±2        C B -2 ≤ x ≤2      D IR

R; O domínio de existência é IR veja aula sobre domínio de existência

 16 Considere as seguintes preposições;

P; Samora Machel foi primeiro presidente de Moçambique independente

Q: Moçambique é um  pais africano

Qual é a escrita simbólica de Samora Machel foi primeiro presidente de Moçambique independente e Moçambique não é um país africano

A. Pᴧq     B~Pᴧp     C~pᴧq   D pᴧ~q

Simbólica	Forma escrita
P	Samora Machel foi primeiro presidente de Moçambique independente
ᴧ	e
~q	Moçambique não é um país africano

Então a escrita simbólica de Samora Machel foi primeiro presidente de Moçambique independente e Moçambique não é um país africano é Pᴧ~q.

 17 Qual das preposições é equivalente a  pᴧ(pᴧ~q)

A. Pᴧ~q     B~Pᴧp     Cpᴧq   D~ pᴧ~q

pᴧ(pᴧ~q)

(pᴧp)ᴧ(pᴧ~q)

pᴧ~q

A preposição pᴧ(pᴧ~q) equivale a pᴧ~q

18 Considere o conjunto M={-2, -1, 0, 1, 3}. Qual é a proposição verdadeira?

A. ∀x ∈ M: ∀ 2x=10     B. ∃x ∈ M: 2x=4  C. ∀x ∈ M: x²+9=17 D. ∃x ∈ M: x² >
x+1

A alternativa “A” é falsa pois não são todos números que pertencentes a M que ao multiplicar por dói o resultado é 10.(Olhando para o conjunto M não existe nem numero)

A alternativa “B” é falsa pois não são Nenhum números que pertencente a M que ao multiplicar por dois o resultado é o resultado 4.

A alternativa “C” é falsa pois não são todos números que pertencentes a M que o seu quadrado somado com nove o resultado é 17. (Olhando para o conjunto M não existe nem numero)

A alternativa “D” é verdadeira pois existe um número que pertencente a M que o seu quadrado é maior que ele mesmo mais 1. (por exemplo 3²>3+1)

 

19. Considere as seguintes expressões;

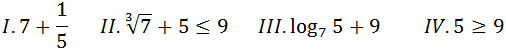
Quais representam designação?

A. II e II        B I e III  C  I e II      D II e IV

As expressões que representam designação são I e III

21. Considere a inequação -|x|<0, qual é a solução ?

A IR+       B IR       C IR-      D ∅

Resolução

-|x|<0

|x|>0

Modulo de qualquer numero é positivo então x pode ser qualquer numero ou
seja x ∈ IR

 22. De quantas maneiras diferentes três amigos podem se posicionar numa fila para tirar uma fotografia.

A 6       B 3       C 9     D 12

Resolução: São permutações de três elementos

P3=3!=3•2•1=6

Três amigos podem se posicionar numa fila para tirar uma fotografia de 6 maneiras diferentes 

23. Um estudante do ISCISA e seleccionado de um grupo de 5 estudantes do curso de administração Hospital e 7 estudantes do curso de Tecnologia Biomédica. Qual a probabilidade do estudante escolhido seja do curso de Tecnologia biomédica?

A. 1/5      B. 5/12        C. 1/7          D. 7/12

P(A)=#(A)/#Total

Casos favoráveis de A “#(A)”são os estudantes do curso de Tecnologia biomédica que são 7.

Casos totais “#Total” é a soma de todos os estudantes do grupo 5 estudantes do curso de administração Hospital mais 7 estudantes do curso de Tecnologia Biomédica ou seja são 12 #total=12

P(A)=#(A)/#Total

P(A)=7/12

A probabilidade do estudante escolhido seja do curso de Tecnologia Biomédica é de 7/12.

 

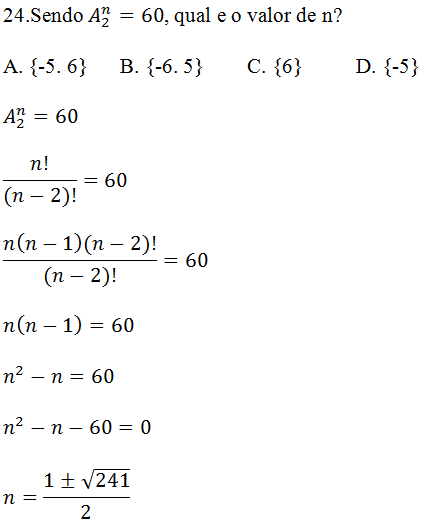
Como a valor de n encontrado não é natural a expressão não tem solução (Veja aula sobre arranjos)

 25. Qual a ordem do termo 4 na sucessão Un=2n-6

A. 5      B. 3        C. 2          D. 6

un=2n-6

4=2n-6

2n=6+4

2n=10

n=10/2

n=5

A ordem do termo 4 na sucessão un=2n-6 é 5

26. Qual o termo gerar da sucessão 2; 6; 18…?

A. 3•2ⁿ-¹     B. 2•3ⁿ-¹             C. 3•3ⁿ-¹                       D. 2•2ⁿ-¹    

Resolução

A sucessão 2; 6; 18…é uma progressão geometria de razão três (r=3) e primeiro termo dois a1=2

E a forma do termo geral de uma PG é an=a1•rⁿ-¹ substituindo a valo de r e a1 temos;

an=2•3ⁿ-¹    

Resposta: o termo geral da sucessão 2; 6; 18… é an=2•3ⁿ-¹  

27. Numa progressão aritmética sabe-se que o quarto termo é 17 o décimo terceiro termo é 62, Quais são respectivamente os valores do primeiro termo e da diferença

A  -5 e 5     B 2 e 5     C 1 e 7

an=a1+(n-1)d

17=a1+(4-1)d

62=a1+(13-1)d

17=a1+3d

62=a1+12d

-17=-a1-3d

62=a1+12d

_________

45=9d

d=45/9

d=5

17=a1+3d

a1=17-3d=17-3•5=17-15=2

O primeiro termo é 2 e a diferença é 5

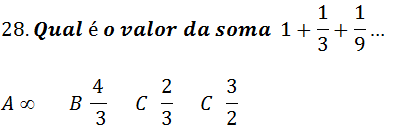
Estamos diante da soma de uma PG infinita com a1= 1 e r =1/3 a soma é dado pela formula;

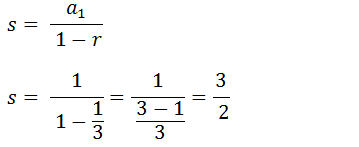
 29. Sabendo que o lucro semanal de venda de automóveis cumpre a ordem (2000, 4000, 8000…), qual é o lucro obtido durante as primeiras 10 semanas?

A.102400       B. 1024     C. 2046     D. 2046000

Resolução: O lucro semanal forma uma progressão geométrica PG de razão 2 com primeiro
termo 2000 e pretendemos o lucro obtido na décima semana.

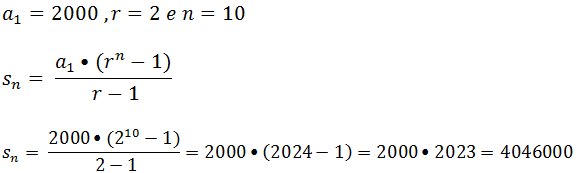
Resposta; O lucro obtido durante as primeiras 10 semanas é de 4046000 (Soma de uma progressão geométrica)

 

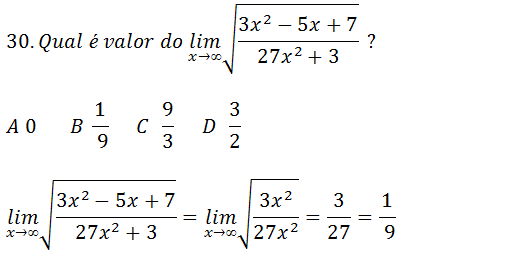
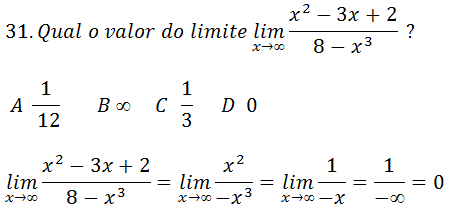
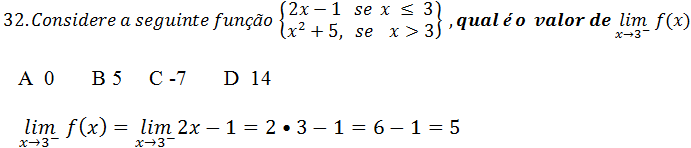
(limites laterais)

33. Qual é a primeira derivada da função f(x)=ln(x²-1)     

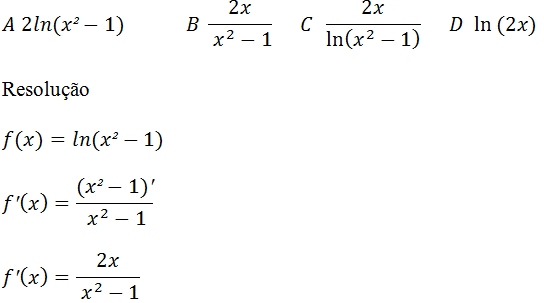
34. Qual é a equação da recta tangente ao gráfico da função f(x)=x³-3x+5 em x=2

A 9x-y+11=0       B 9x+y+11=0      D 9x-y-11=0       D -9x+y-11=0

A equação da recta é y-yo=m(x-xo)

xo=1

yo=f(xo)= 2³-3•2+5=8-6+5=7

m=f’(xo)

f(x)=x³-3x+5

f’(x)=3x²-3

m=f’(xo)= 3•2²-3=12-3=9

y-yo=m(x-xo)

y-7=9(x-2)

y-7=9x-18

y-9x+11=0

A equação da recta tangente ao gráfico da função f(x)=x³-3x+5 em x=2 é
y-9x+11=0
35. A Maria decompôs o número 20 em duas parcelas x e y, Quais são esses valores de modo que o produto seja máximo?

A x=10 e y=10     B x=8 e y=12    C x=0 e y=20    D x=4 e y=16

x+y=12

P=x•y

A partir da primeira equação podemos escrever y=20-x em então o produto de x e y pode ser escrito;

P=x•(20-x)

P=20x-x²

Uma função é máxima em um ponto se a derivada nesse ponto for zero

P’=20-2x

P’=0

20-2x=0

2x=20

x=10

y=20-x=20-10=10

Resposta x=10 e y=10