Derivada da função arctan(x) e arcctg(x)

Derivada de Funções Trigonométricas Inversas: Arctangente e Arcocotangente

Após estudarmos as derivadas das funções inversas seno e cosseno, vamos agora nos aprofundar nas derivadas das funções inversas tangente e co-tangente.
Primeiro, veremos e demonstraremos as fórmulas das derivadas das funções:

• y=arctan⁡(x))
• y=arcotg(x)

Derivada da função inversa de tangente (Derivada de função arctangente)

y=acrtan(x)

Derivada da função y= acrtan(x) demonstração

Para calcular a Derivada da função y= acrtan(x) vamos colocar a função em função de y conforme sabemos se y= acrtan(x) então x=tan(y).

x=tan(y)

Tendo a função nessa forma já podemos derivar uma vez que conhecemos a derivada da função trigonométrica tangente tan(y) e a derivada de x, então derivaremos ambos membros;

x’=(tan(y))’

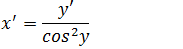
Vamos isolar a derivada da função y (isolar y’) passando o cos²(y) para multiplicar no outro membro

y’=x’cos² y

Vamos recorrer a identidade trigonométrica fundamental para calcular o valor de cos²(y) em relação a x.

sin²y+cos²y=1

Dividindo ambos membros por cos²y temos ;

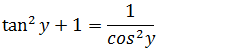
Vamos isolar o cos²y ao quadrado

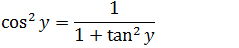
No segunda passa dessa demonstração dissemos que x=tan(y) então onde tem tan(y) iremos substituir por x pois tan(y)=x

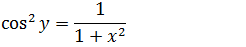
Então na expressão da derivada da função inversa (y’=x’cos² y) onde tem cos²(y) iremos substituir por essa expressão e assim temos a derivada da função arcsenx

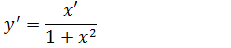
Derivada da função inversa de co-tangente (Derivada de função arcco-tangente)

y=acrctg(x)

Tal como fizemos para calcular a derivada da função arctan(x), para a  calcular a Derivada da função y= acrctg(x) vamos colocar a função em função de y conforme sabemos se y= acrctg(x) então x=ctg(y).

x=ctg(y)

Vamos derivar ambos membros;

x’=(tan(y))’

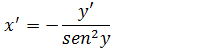
Vamos isolar y’passando o sen²(y) para multiplicar no outro membro;

y’=-x’sen²y

recorrendo a identidade trigonométrica fundamental para calcular o valor de sen²(y) em relação a x.

cos²y+ sin²y=1

Dividiremos os dois ambos membros por sen²y fazendo isso temos ;

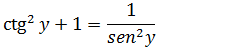
Vamos achar a expressão de sen²y para substituímos na expressão da derivada da função inversa

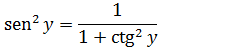
Como x= ctg(y) então onde tem ctg(y)iremos substituir por x pois ctg(y)=x

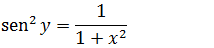
Então na expressão da Derivada da função inversa (y’=-x’sen² y) onde tem sen²(y) iremos substituir por essa expressão e assim temos a derivada da função arcctg(x)

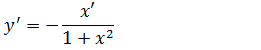
Formula de derivada de funções trigonométricas inversas arctanx e arcctgx

De acordo com as demonstrações acima de derivada de funções trigonométricas inversas temos;

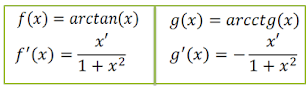
Exercício práticos derivadas de funções inversas arctangente e arcco-tangente

a)Calcule a derivada da função y=arctan(5x)

Estamos diante de uma função inversa então para derivar vamos usar a forma da derivada da função inversa arctangente.y=arctan(u), y’=u’/(1+u²) aplicando a forma temos;

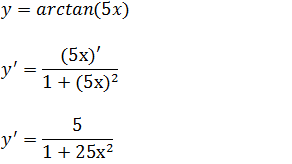
b)Calcule a derivada da função y=arcctg(-2x)

Vamos usar a forma da derivada da função arcctg(u) sabemos que se y=arcctg(u) a sua derivada é  y’=-u’/(1+u²) aplicando a forma ;

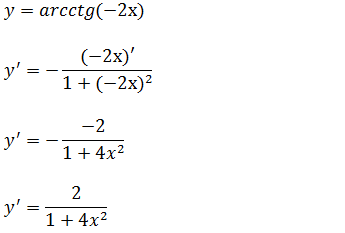
c)Determine a derivada da função y=arcctg(x²+1)

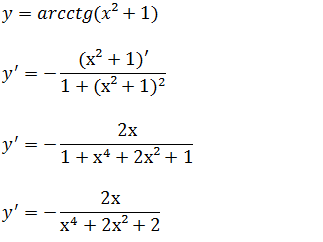
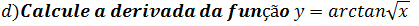
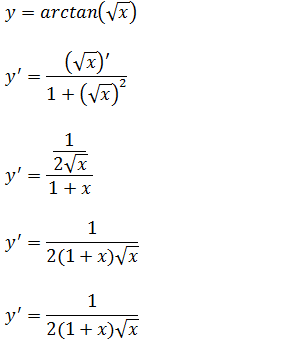
e)Encontre a derivada da função y=(x+2) arctan(x)

Estamos diante de um produto de função então para derivar vamos usar a formula da derivada do produto “regra do produto”

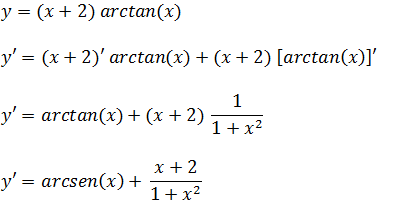
Vamos derivar de forma imediata aplicando a formula da derivada de arcctg(u);

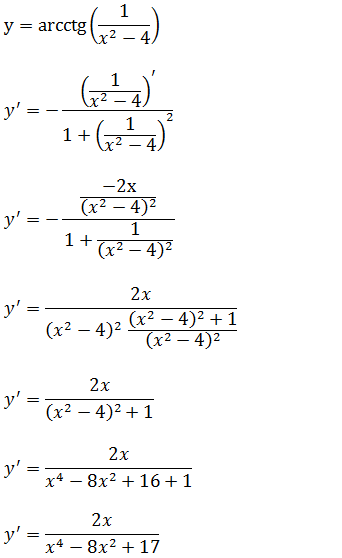
g)Ache a derivada da função y=arctan[ln(x)]

Vamos aplicar a forma da derivada da função arctan(u) ” y’=u’/(1+u²) “tendo em conta que para este exercício o nosso u e ln(x) então precisaremos de conhecer a derivada da função ln(x);

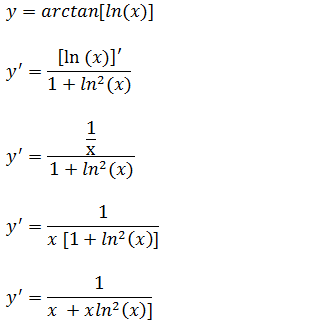
Derivada da função arctan(x) e arcctg(x) exercícios para praticar

Calcule a derivas das funções trigonométricas inversas abaixo;