Dinâmica (força resultante e decomposição de forças )

Dinâmica

No primeiro capítulo vimos a cinemática onde estudamos os movimentos, veja que na cinemática não se importávamos com a causa do movimento aqui na dinâmica nos teremos em conta a causa do movimento.

Cinemática ramo da física que estuda o movimento sem ter em conta a causa do movimento.

Dinâmica ramo da física que estuda o movimento tendo em conta a causa do movimento.

O que causa o movimento?

Podíamos responder essa questão de forma imediata mais convêm analisamos para que possamos compreender de forma excepcional. Imaginemos um caro parado para o caro entrar em movimento nos podemos; Empurrar o caro ou ligamos o motor e colocarmos o carro em movimento (conduzir) Veja que tanto numa assim como noutra forma nos sempre aplicamos força sobre o carro para que ele entre em movimento no primeiro caso nos aplicamos uma força mecânica e no segurando nos aplicamos a força do motor (força motorica). Isso nos vela a concluir que a causa do movimento é a força.
Para alem de termos causa movimento temos o efeito do movimento que chamamos de aceleração.

Tipos de força

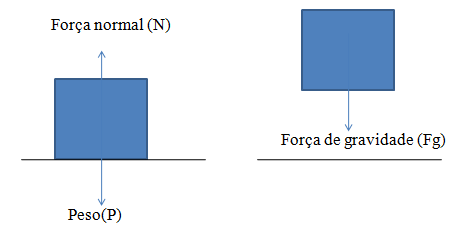
Força de gravidade é a força que os corpos são traídos para a terra;
Força de normal é a força com que as superfícies se opõe a uma forca nelas aplica; Peso representa a força que nos exerceremos sobre as superfícies; Outras forças estudaremos mais afrete durante a abordagem do tema.

Força resultante

Força resultante é uma força capaz de representar geometricamente assim como em termos de modulo um conjunto de força.

Sistema de forças e força resultante

1. Força na mesma direcção e sentido

Uma víeis que as forças estão na mesma direcção e sentido a força resultante será a soma das duas forças. Fr=F1+F2 E tem a mesma direcção que elas ou seja;

2. Forças na mesma direcção e sentidos contrários sentido.

A força resultante será a diferença das duas forcas; Fr=F2-F1

3. Forças em direcções contrários.

4. forças em direcções contrários que forma ângulo de 90ᵒ

A força resultante será uma força que vai para cima e ao mesmo tempo vai para a direita vindo do lado esquerdo. O seu modulo pode ser obtido pelo teorema de Pitágoras;

5.A força resultante terá que ir obliquamente do lado direito e terá módulo igual;

Exercícios de aplicação

Para  os sistemas abaixo determine a força resultante usando os métodos convenientes.

Forças na mesma direcção e sentindo contrario a resultante é a diferença;

Fr=F2-F1

Fr=22-16

Fr=6N

As forças estão na mesma direcção e sentido a resultante será a soma;

Fr=F2+F1

Fr=5+9

Fr=14N

Visto que as forças formam um ângulo recto (90ᵒ) usaremos o teorema de Pitágoras para ter a resultante;

   Podemos obter a força resultante recorrendo a fórmula:

α é o ângulo entre as duas forças Primeiro vamos obter o ângulo entre as duas forças (o ângulo entre as duas forças não é 60ᵒ) para obter o ângulo vamos ter em conta que um ângulo raso tem 180ᵒ e para o ângulo entre as duas forças completar um ângulo raso falta 60ᵒ o ângulo entre as duas forças será α=180ᵒ-60ᵒ=120ᵒ agora vamos substituir esses valores na fórmula;

Decomposição de forças

Se nós tivermos uma força ou mais forças actuando obliquamente sobre um corpo nos podemos decompor essas forças em duas componentes uma verticar Fy e uma Horizotal Fx .

Visto que Fx, Fy, F formam um triângulo com, hipotenusa F e com ângulo α as componentes Fx e Fy podem ser obtidos por:

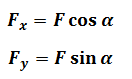
Exercício

Para a figura abaixo determine a componente vertical (Fy) e horizontal (Fy) da força F

Resolução Vamos esquematizar

---