Inequações exponenciais

O que são Inequações exponenciais

Inequações exponenciais são inequações onde a variável aparece no expoente, são inequações do tipo;

a)3^x+2 <9

b)8^x-3 > 32^x

c)4^x-4^x+2+30 ≥ -2

d)2^2x-5•2^x+3 ≥-1

Como resolver de inequações exponenciais

A resolução de inequações exponenciais é feita tendo em conta que a>1 e 0 < a <1.

Resolução de Inequações exponenciais com base menor que 1 (a > 1)

Nesses quando onde a base é maior que 1 (a>1) não alteramos o sinal original da inequação ou seja.

a^x>a^y

x>y

Resolução de Inequações exponenciais com base menor que 1 e maior que zero (0<a <1)

a^x > a^y

x<y

“ Quando a base é menor que 1 para resolver a inequação devemos mudar de sentido do sinal de comparação se for > passa a ser < , se for ≤ mudamos para ≥ e vice versa.”

Porque em uma inequação exponencial quando 0 < a <1 invertemos o sentido ?

Sabemos que uma função exponencial do tipo f(x)=a^x com 0<a<1 é uma função decrescente, o que quer dizer que quando os valores de x aumenta a função vai tomando valores cada víeis mais pequenos, essa é a razão que nos leva a inverter o sinal quando da inequação exponencial sempre que 0<a<0.

Resolução de exercícios sobre inequações exponenciais

a)2^x>4

Iremos primeiramente decompor o 4 em uma potência de babe 2; (4=2²)

2^x>2²

Como temos as mesma base, e é menor que 1 para achar a solução iremos mater o sinal.

x>2

Solução ; x>2

b)27^x+1>9^x

De forma análoga ao primeiro exercício, para achar a solução dessa inequação exponencial primeiro vamos decompor de modo a termos a mesma base em ambos membros

27^x+1>9x

(3³)^x+1>3^2x

3^3x+3>3^2x

3x+3>2x

3x-2x>-3

x>-3

c)5^x>7^x

Note; mudamos de sentido porque a base é menor que 1.

Como a base é menor que 1 para resolver a inequação exponencial vamos mudar de sinal e assim temos;

x < 3

Solução; x < 3

Resolução

Note que fazendo a decomposição; 16=2⁴ e 8=2³ assim podemos escrever;

Vamos transformai a raiz em potencias, (O índice da raiz vai passar a dividir o expoente do radicando)

Como temos bases iguais vamos trabalhar com os exponentes

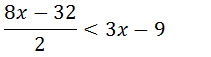
4x-16<3x-9

4x-3x<-9+16

x<7

f)4^x-4^x+2+28≥-2

4^x-4^x+2+28≥-2

4^x-4^x •4²≥-2-28

4^x-4^x•16≥-30

4^x (1-16)≥-30

4^x (-15)≥-30

-4^x•15≥-30

4^x•15≤30

4^x≤30/15

4^x≤2

2^2x≤2¹

2x<1

x<1/2

h)4^x-3•2^x+2+30<-2

4^x-3•2^x+2+30<-2

Vamos decompor 4, (4=2²) e aplicar as propriedades de potência para 2^x+2, ou seja separa transformar a soma dos expoentes em um produto (2^x+2=2^x•2²), fazendo a substituição na inequação temos;

(2² )^x-3•2^x •2²+30+2<0

2^2x-12•2^x+32<0

Seja 2^x=t

t²-12t+32<0

Agora temos uma inequação quadrática, já vimos como resolver a inequações quadráticas nas aulas anteriores. Iremos usar o método trafico para resolver a inequação onde primeiro calcularemos os zeros que são t₁=4 e t₂=8

Como o valor de “a” é positivo a inequação tem parábola positiva

Queremos onde é menor que zero podemos ver no gráfico que é no intervalo de 4 a 8 ou seja;

t>4 e t<8

Como t=2^x vamos substituir os “t” por essa expressão e achar a solução da inequação exponencial

 2^x>4   e  2^x<8

2^x>2²   2^x<2³  

x>2        x<3

A solução da nossa equação exponencial é x>2 e x<3 ou seja;

Sol;  2<x<3

---

---

---