Depois de termos aprendido a resolver as equações quadráticas, e as inequações quadráticas agora vamos aprender sobre as funções quadráticas onde aprenderemos;
– O que são funções quadráticas
– Como representar graficamente uma função quadrática
O que são funções quadráticas
Função quadráticas são funções do tipo f(x)=ax2+bx+c
Exemplos de função quadráticas
EX1; f(x)=2x2+5x+4
EX2; f(x)=-4x2-7x+1
EX3; f(x)=x2-5x+3
EX4; f(x)=x2+34
EX5; f(x)=8x2
EX6; f(x)=-x2
Como é que é o gráfico de uma função quadrática (função do segundo grão)
O gráfico de uma função quadrática (função do segundo grão) é sempre uma parábola, que pode estar voltado para cima ou para baixo;
Quando é que a função quadrática tem parábola voltado para cima e quando esta voltado para baixo ?
A função quadrática tem parábola voltada para cima se o valor de “a” for positivo
A função quadrática tem parábola voltada para abaixo se o valor de “a” for negativo
Como representar graficamente uma função quadrática
Gráfico de uma equação quadráticas com a > 0 e ∆ > 0
Como “a” menor que zero significa que a função tem parábola volta para cima, e como delta é positivo tem raízes reais o nesses casos o gráfico será ;
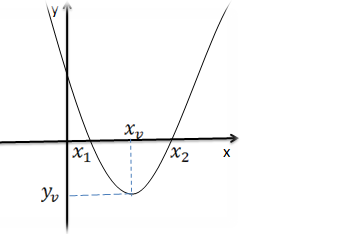
Gráfico de uma equação quadráticas com a < 0 e ∆ > 0
Como o valor de a < 0 significa que a função tem parábola volta para baixo, e como delta é positivo a função tem zeros, nesses casos o gráfico terá a seguinte configuração;
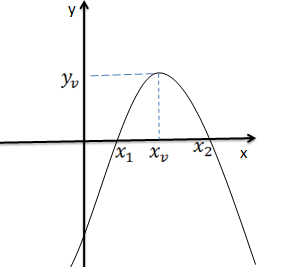
Gráfico de uma equação quadráticas com a > 0 e ∆ < 0
Como o valor de “a” é maior que zero a função tem parábola volta para cima, e como delta é menor que zero a equação não raízes, o que significa que a função não tem zeros o gráfico será:
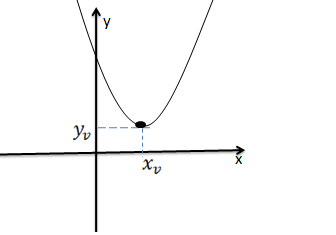
Gráfico de uma equação quadráticas com a < 0 e ∆ < 0
Nesses casos a função tem parábola volta para baixo, e como delta é menor que zero a equação não raízes então não irá atravessar o eixo das abcissa.
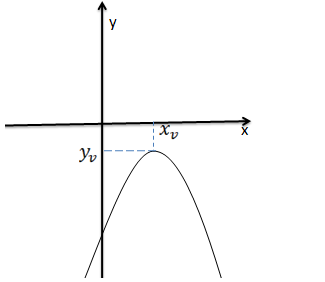
Coordenadas de vértices de uma equação quadrática
Quando vamos de coordenadas de Coordenadas de vértices de uma equação quadrática estamos a falar de xv e yv.
X vértice (xv) representa o valor da abcissa o valor da abcissa onde o gráfico se divide em duas partes iguais. E pode ser calculado a partir de;
O valor do x vértice (xv) também pode ser achado a partir da media aritmética das raízes;
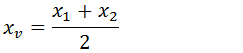
y vértice (yv) representa o valor máximo ou mínimo da função.
O yv representa o valor máximo da função se o valor de “a” for menor que zero.
O yv representa o valor mínimo da função se o valor de “a” for positivo (maior que zero).
O valor de yv pode ser calculado a partir da fórmula;
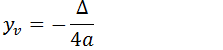
Coordenadas de vértices
As coordenadas de vértices são (xv,yv)
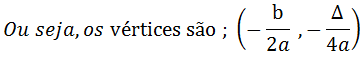
Dicas práticas para representar uma equação do segundo grão
1.Calcular os valores de xv e yv
Os valores de xv e yv são calculados a partir das fórmulas;
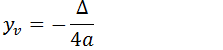
2.Calcular os zeros da função(x1 e x2)
As raízes (os zeros) da equação são calculadas a partir da fórmula;
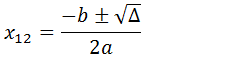
3. Identificar ou calcular o valor da ordenada na origem
Devemos ter sempre em mente que o valor de “c” representa o valor da ordenada na origem ( valor de y quando x=0)
4. Analisar se o gráfico tem parábola voltada para cima ou para baixo
- Se o valor de “a” for maior que zero o gráfico esta voltado para cima se for negativo esta voltado para baixo.
5.Desenhar o gráfico
Depois de ter já todos pontos é só representar esses dados no nos sistema de cordenadas XOY e assim temos o gráfico da equação quadrática.
Exercícios resolvidos para representar gráficos de funções quadráticas
1.Represente graficamente a função;
a) f(x)=x2-5x+6
Resolução
f(x)=x2-5x+6
a=1, b=-5, c=6
Primeiro vamos calcular as coordenadas de vértice
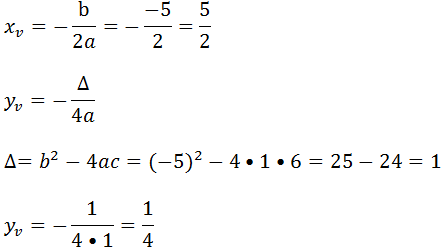
Agora vamos calcular as raízes
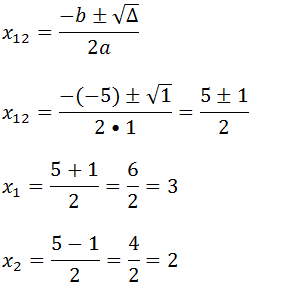
A ordenada na origem
f(0)=02-5•0+6=6
Nota; A ordenada na origem é sempre o valor de “c”
Como o valor de “a” é positivo a parábola terá concavidade voltada para cima e tendo em conta os valores das raízes e dos vértices o gráfico fica;
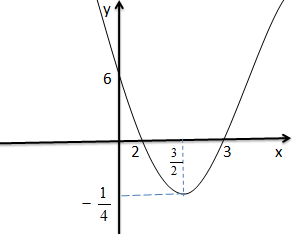
b) Faça o gráfico da função; f(x)=-2x2+8x+10
Resolução
a=-2 , b=8, c=10
Primeiro vamos calcular as coordenadas de vértice
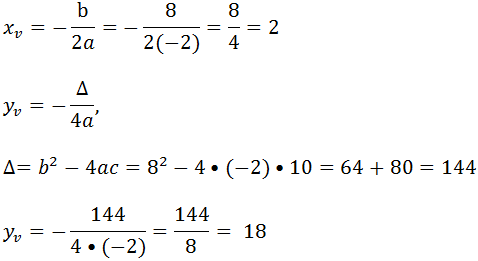
Agora vamos calcular as raízes
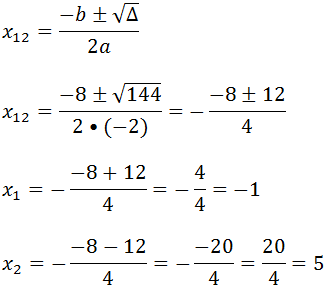
A ordenada na origem
A ordenada na origem é o valor de “c” que é 10
Como o valor de “a” é negativo a parábola terá concavidade voltada para baixo assim o gráfico fica;
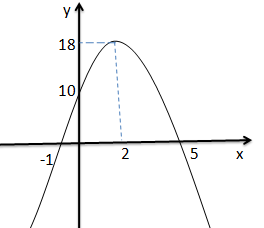
c)Represente graficamente a seguinte função quadrática;
f(x)=3x2+6x+4
Resolução
a=3 , b=6, c=4
seguindo o mesmo raciocino vamos calcular as coordenadas de vértice
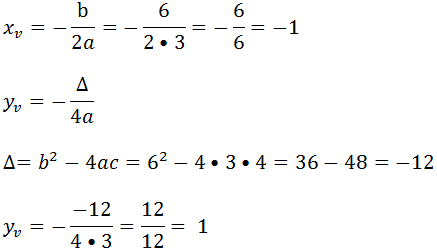
Calculo das raízes
Como delta deu o valor negativa (∆=-12<0) significa que a função não tem raízes
Ordenada na origem
A ordenada na origem é 4 ( o valor de “c” )
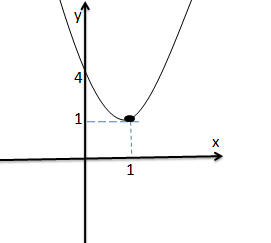
Como o valor de “a” é positivo a parábola terá concavidade voltada para cima e tendo em conta que a ordenada na origem é 4 e os vértices são (1,1) e que a equação não tem zeros o gráfico fica.
Exercícios sobre funções quadráticas para praticar
Represente graficamente as seguintes funções quadráticas;
a)g(x)=x2-9
b) f(x)=-3x2+15x-18
c) f(x)=4x2+x+2
d)f(x)=-x2+10x-25
e)f(x)=x2
f)f(x)=100x2