Inequações quadráticas

Inequações quadráticas são inequações do segundo grão, ou seja:

Inequações quadráticas são inequações do tipo ax²+bx+c≥0 ou ax²+bx+c≤0 , Onde a, b e c são números reais e a é diferente de zero

Exemplos de inequações quadráticas

a)2x²-x+4≥0

b)x²-3x >0

c)x²<0

d)x²-8> 0

2. Métodos de resolução de uma inequação quadrática : ax²+bx+c≥0

Nesse artigo iremos ver a resolução de Inequações quadráticas usando:

2.1.Método gráfico;

2.2.Método analítico (usando tabela para estudar o sinal).

2.1.1.Resolução de Inequações quadráticas usando método gráfico;

ax²+bx+c≥0

Para a resolução de uma inequação quadrática usamos os seguintes:

Fazemos f(x)=ax²+bx+c=0
De Seguida calculamos os valos de x₁ e x₂
Fazemos um esboço de f(x)

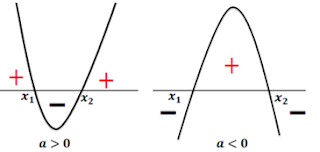
* Por fim analisar onde f(x) ≥0 (conforme o enunciado)

Exemplo de resolução de inequações quadráticas usando o método gráfico

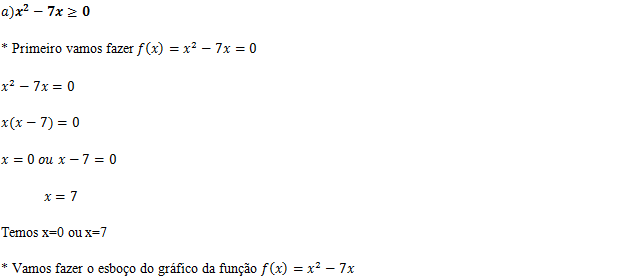
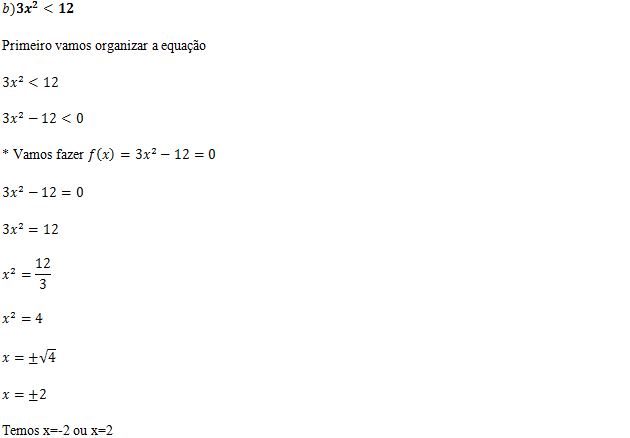
(queremos onde é menor que zero “Onde é negativo”)

R:[-2;2]

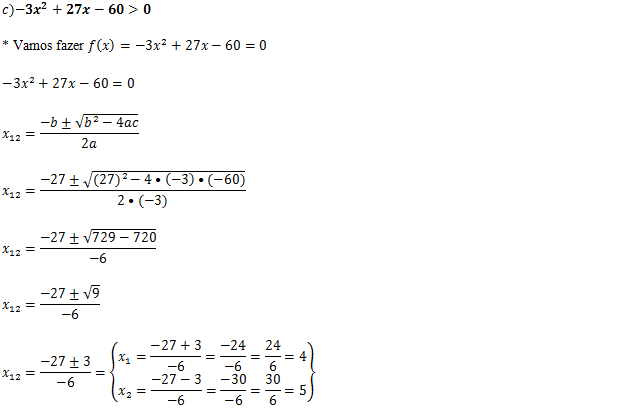
R:[4;5]

Resolução de Inequações quadráticas usando método analítico (usando tabela para estudar o sinal).

Para a resolução de uma inequação quadrática usando o método de tabela primeiro;

* Fazemos a fautorizar a expressão

* De Seguida fazemos a tabela

x	-∞		x₁		x₂		+∞
a(x-x₁)		S1		S11		S111
(x-x₂)		S2		S22		S211
P		S’		S’’		S’’’

Nota: Ondetem S vamos analisar o sinal no intervalo dado

Exemplo de resolução de inequações quadráticas usando o método analítico

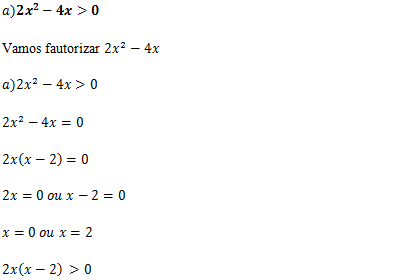
Vamos construir a tabela para resolver a inequação

x	-∞	0	2	+∞
2x
x-2
P

Para preencher a tabela :

Vamos escolher um numero no intervalo ] -∞ : 0[ Escolheremos -3 (podes escolher outro desde que esteja no intervalo)

2x=2•(-3)=-6 (O sinal desse numero é negativo)

x-2=-3-2=-5 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (-×-=+) “P tem sinal positivo nesse intervalo”

x	-∞		0	2	+∞
2x		–
x-2		–
P		+

Vamos escolher um numero de menos ] 0 : 2[ Escolheremos 1 (podes escolher outro desde que esteja no intervalo)

2x=2•1=2 (O sinal desse numero é positivo)

x-2=1-2=-1 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (+) × (-)=- “P tem sinal negativo nesse intervalo”

x	-∞		0		2	+∞
2x		–		+
x-2		–		–
P		+		–

Vamos escolher um numero de menos ] 2 : +∞ [ Escolheremos 4 (podes escolher outro desde que esteja no intervalo)

2x=2•4=8 (O sinal é positivo)

x-2=4-2=2 (O sinal é positivo)

O Sinal de P será o produto entre os dois sinais (+) × (+)=+ “P tem sinal positivo nesse intervalo

x	-∞		0		2	+∞
2x		–		+		+
x-2		–		–		+
P		+		–		+

Sol: ]- ∞;0[U]2;+ ∞[
Olhado para nossa inequação “2x(x-2) >0”queremos onde (P) é maior que zero ou seja queremos onde é positivo Olhando a tabela podemos ver facilmente que (P) é positivo no intervalo de :]- ∞;0[U]2;+ ∞[

Sol: ]- ∞;0[U]2;+ ∞[

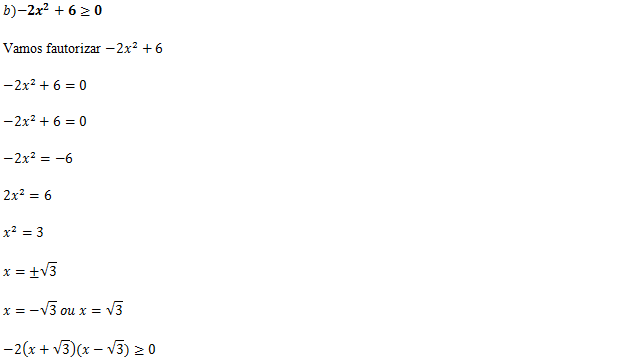
x	-∞	-√3	√3	+∞
-2(x+√3)
(x-√3)
P

Para preencher a tabela :

Vamos escolher um numero de menos ] -∞ : -√3[ .Escolheremos -100 (podes escolher outro desde que esteja no intervalo)

-2(x+√3)= -2(-100+√3)= 200-2√3 (O sinal desse numero é positivo)

(x-√3)= -100-√3 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (+)×(-)=- “P tem sinal negativo nesse intervalo”

x	-∞		-√3	√3	+∞
-2(x+√3)		+
(x-√3)		–
P		–

Vamos escolher um numero no intervalo ] -√3 : √3 [ .Escolheremos 0 (podes escolher outro desde que esteja no intervalo)

-2(x+√3)= -2(0+√3)= -2√3 (O sinal desse numero é negativo)

(x-√3)= 0-√3=-√3 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (-)×(-)=+ “P tem sinal positivo nesse intervalo”

x	-∞		-√3		√3	+∞
-2(x+√3)		+		–
(x-√3)		–		–
P		–		+

Vamos escolher um numero no intervalo ] √3 : +∞ [ .Escolheremos 5 (podes escolher outro desde que esteja no intervalo)

-2(x+√3)= -2(5+√3)= -10-2√3 (O sinal desse numero é negativo)

(x-√3)= 5-√3 (O sinal desse numero é positivo)

O Sinal de P será o produto entre os dois sinais (-)×(+)=- “P tem sinal negativo nesse intervalo”

x	-∞		-√3		√3		+∞
-2(x+√3)		+		–		_
(x-√3)		–		–		+
P		–		+		–

Olhado para nossa inequação “-2(x+√3)(x-√3)≥0”queremos onde (P) é maior ou igual a zero ou seja queremos onde é positivo incluindo onde é zero Olhando a tabela podemos ver facilmente que (P) é positivo no intervalo de :[-√3;√3]

Sol :[-√3;√3]

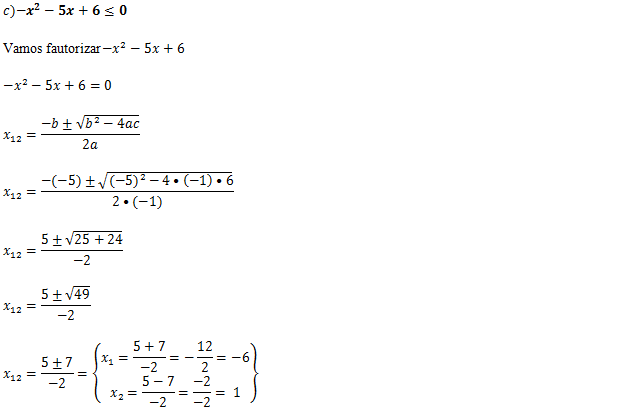
-(x+6)(x-1)≤0

x	-∞	-6	1	+∞
-(x+6)
x-1
P

Para preencher a tabela :

Vamos escolher um numero no intervalo ] -∞ : -6 [ .Escolheremos -10 (podes escolher outro desde que esteja no intervalo)

-(x+6)= -(-10+6)=10-6=4 (O sinal desse numero é positivo)

(x-1)= -10-1=-11 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (+)×(-)=- “P tem sinal negativo nesse intervalo”

x	-∞		-6	1	+∞
-(x+6)		+
x-1		–
P		–

Vamos escolher um numero no intervalo] -6 : 1 [ .Escolheremos 0 (podes escolher outro desde que esteja no intervalo)

-(x+6)= -(0+6)=-6 (O sinal desse numero é Negativo)

(x-1)= 0-1=-1 (O sinal desse numero é negativo)

O Sinal de P será o produto entre os dois sinais (-)×(-)=- “P tem sinal positivo nesse intervalo”

x	-∞		-6		1	+∞
-(x+6)		+		–
x-1		–		–
P		–		+

Vamos escolher um numero no intervalo] 1 : ∞ [ .Escolheremos 3 (podes escolher outro desde que esteja no intervalo)

-(x+6)= -(3+6)=-9 (O sinal desse numero é Negativo)

(x-1)= 3-1=2 (O sinal desse numero é Positivo)

O Sinal de P será o produto entre os dois sinais (-)×(+)=- “P tem sinal negativo nesse intervalo”

x	-∞		-6		1		+∞
-(x+6)		+		–		_
x-1		–		–		+
P		–		+		–

Olhado para nossa inequação “-(x+6)(x-1)≤0”queremos onde (P) é menor ou igual a zero ou seja queremos onde é negativo incluindo onde é zero(Onde não é negativo) Olhando a tabela podemos ver facilmente que (P) não é negativo no intervalo de :]- ∞;-6]U[1;+ ∞[

Sol:]- ∞;-6]U[1;+ ∞[