Derivada de funções paramétricas

Derivada de funções paramétricas

Seja  y=f(t) e x=g(t) nesse caso podemos afirmar que x e y estão dadas na forma paramétrica.

Como achar a derivada de uma função dada na forma paramétrica?

Para achar a derivada da função dy/dx temos que primeiro achar a derivada de y (dy)  e depois acharmos a derivada de x (dx)e pois a fazer a razão entre essas derivada.

Como achar a derivada de dy

A derivada dy é obtida derivando ambos membros da função y=f(t)

dy=df(t)

Como achar a derivada de dx

A derivada dx é obtida derivando ambos membros da função x=g(t)

dx=dg(t)

Então a derivada da função paramétrica dy/dx pode ser escrita como;

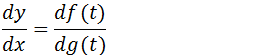
Exercícios de derivada de funções dada na forma paramétrica

1.Seja dado a seguinte função na forma paramétrica

y=t+1

x=2t²+4t

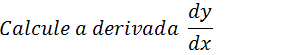
Primeiro vamos calcular dy

dy=d(t+1)

dy=tdt

Agora vamos calcular dx

dx=d(2t²+4t)

dx=(4t+4)dt

Agora podemos finalmente encontrar dy/dx

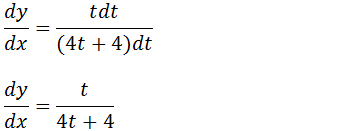
2.Seja dado a seguinte função na forma paramétrica

y=sen(t)

x=cos(t)

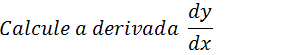
Primeiro vamos calcular dy

dy=d(sen(t))

dy=cos(t)dt

Agora vamos calcular dx

dx=d(cos(t))

dx=-sen(t)dt

Agora podemos finalmente encontrar dy/dx

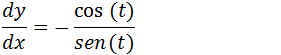
3.Seja dado a seguinte função na forma paramétrica

y=(t⁴-4t)³

x=5t²-t

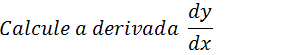
seguindo o mesmo procedimento Primeiro vamos calcular dy

dy=d(t⁴-4t)³

dy=3(t⁴-4t)² d(t⁴-4t)

dy=3(t⁴-4t)² (4t³-4)dt

Agora vamos calcular dx

dx=d(5t²-t)

dx=(10t-1)dt

Agora podemos finalmente encontrar dy/dx

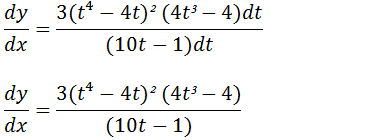
Derivada de segunda ordem para funções dadas na forma paramétricas

Para acharmos a derivada de segunda ordem de uma função dada na forma implícita devemos terá primeira derivada da função paramétrica dy/dx e ter também derivada dx dai fazer a razão entre a função d(dy/dx) e a função dx

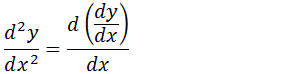
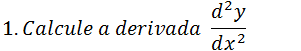
Sendo y=5t²+3t  e  x=6t⁴-7 t²

Para achar a derivada dessa função paramétrica de segunda ordem vamos usar a forma da derivada da função paramétrica de segunda ordem;

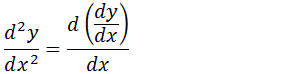
Para facilitar o cálculo dessa derivada primeiro vamos calcular a derivada dy/dx

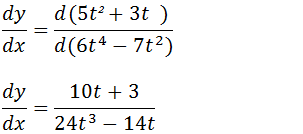
Agora vamos usar a forma;

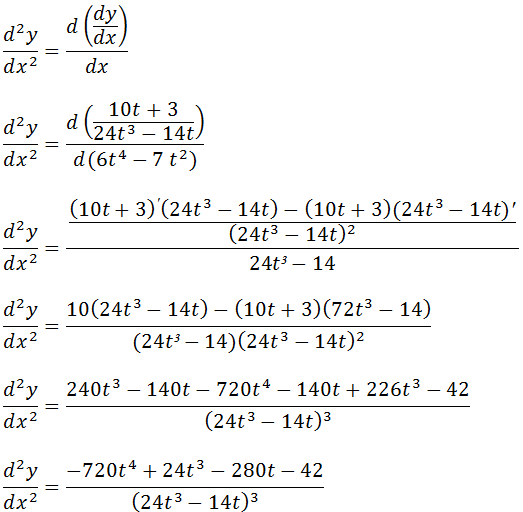
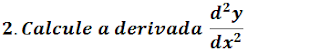
Sabendo que y=4sen(t)+3t  e  x=-2cos(t)-6t

Para achar a derivada dessa função paramétrica de segunda ordem vamos usar a forma da derivada da função paramétrica de segunda ordem;

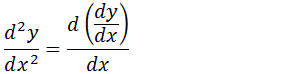
Tal como fizemos no primeiro exercícios para facilitar o cálculo dessa derivada primeiro vamos calcular a derivada dy/dx

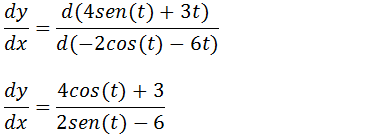
Agora vamos substituir na fórmula;

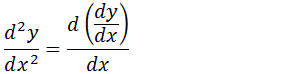
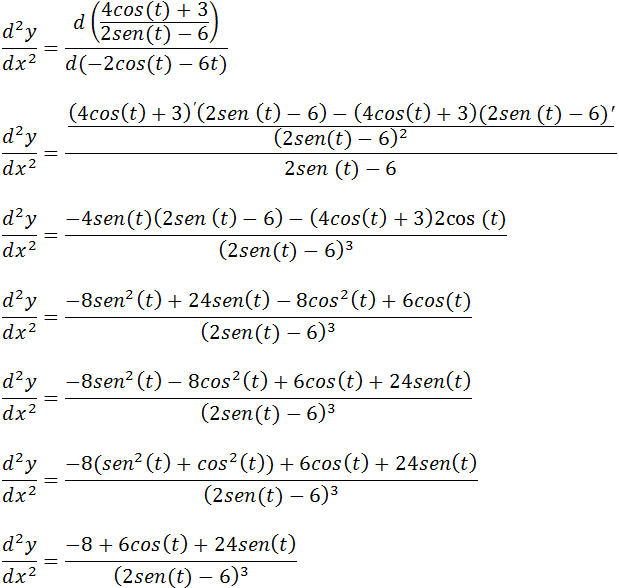
Exercícios para praticar derivada de funções dada na forma paramétricas

1.Seja dado a seguinte função na forma paramétrica

y=3t²+3t

x=3t²-4t

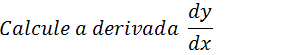
2.Seja dado a seguinte função na forma paramétrica calcule dy/dx

y=sen(t²)+3t   e  x=sen(t)-4cos(t)

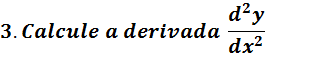
Sendo y=5t⁴+3t²+2  e  x=8t³-5 t²

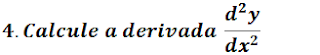
Sabendo que y=asen(t) e  x=bcos(t)

---