
Probabilidades
A probabilidade de um acontecimento representa as chaces desse determinado acontecimento ocorrer. A probabilidade de um acontecimento qualquer calcula-se pela razão entre os casos favoráveis desse acontecimento e os casos possíveis.

Exercícios de aplicação
1.Da o conjunto (1,2,3,4,5,6,7,8) é escolhido aleatoriamente um numero determine a probabilidade de;
a) O número escolhido for par
b) O número escolhido for múltiplo de 3
c) O numero escolhido for menor que seis
Resolução
a) A probabilidade é a razão entre os casos favoráveis e os casos totais, os casos totais são oito (1,2,3,4,5,6,7,8) e para o numero ser par os casos favoráveis serão os números pares do nosso conjunto que são quatro nomeadamente (2,4,6 ,8)

b) Para o número escolhido for múltiplo de 3 os casos favoráveis são (3,6) e os casos possíveis permeassem 8 múltiplo de três

c) Para o número escolhido for menor que 6 os casos favoráveis são todos os números d conjunto que são menores que 6 “(1,2,3,4,5)” que são 5 e os casos possíveis permeassem 8 múltiplo de três

2.Numa urna com 7 bolas brancas e 5 bolas brancas são retiradas simultaneamente duas bolas determine;
a) A probabilidade de se extrair duas bolas brancas
b) A probabilidade de se extrair duas bolas vermelhas
c) A probabilidade de se extrair duas de cores diferentes
d) A probabilidade de se extrair duas da mesma cor
Resolução
a) A probabilidade de se extrair duas bolas brancas é dada por;

Para determinar #casos favoráveis de (duas bolas brancas) vamos ter em conta o número total de bolas braças que temos e nesses queremos duas

Para determinar #casos favoráveis de (duas bolas) vamos ter em conta o número total de bolas que temos(esse numero é a soma de todas as bolas que temos) e nesses queremos duas
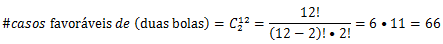
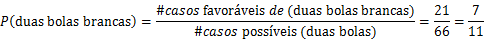
R: A probabilidade de se extrair duas bolas brancas é 7/11
b) A probabilidade de se extrair duas bolas vermelhas é dada por;

R: A probabilidade de se extrair duas bolas vermelhas é 5/33
c) Para determinar a probabilidade de se extrair duas de cores diferentes temos :

Para determinar #casos favoráveis de (duas bolas de cores diferentes) temos que saber que as bolas serão diferentes se uma for branca e a outra for vermelha.
O que significa que nas 7 bolas brancas vamos extrai uma e nas 5 bolas vermelhas vamos extrair uma

R: A probabilidade de se extrair duas bolas de cores diferentes é 35/66
d) Para determinar a probabilidade de se extrair duas da mesma cor

Para determinar #casos favoráveis de (duas bolas da mesma cor) temos que saber que as bolas serão da mesma cor se as duas bolas forem branca ou se as duas bolas forem vermelhas.
O que significa que nas 7 bolas brancas vamos extrai duas ou nas 5 bolas vermelhas vamos extrair duas.

R: A probabilidade de se extrair duas bolas da mesma cor é 31/66
Propriedades da probabilidade e definição axiomática
a)A probabilidade de um acontecimento certo é igual a 100%
P(U)=100%
b)A probabilidade de um acontecimento impossível é igual a zero
P(ø)=0
c) Acontecimentos contrários

U=A+Ᾱ
P(U)=P(A)+(Ᾱ)
P(A)=P(U)-P(Ᾱ)
Sabemos queA probabilidade de um acontecimento certo é igual a 100%=1
P(A)=1-P(Ᾱ)
d)Acontecimentos incompatível

AuB=A/B+A∩B+B/A
AuB=A-(A∩B)+A∩B+B-(A∩B)
AuB=A +B-(A∩B)
P(AuB)=P(A) +P(B)-P(A∩B)
e)De A e B forem acontecimentos disjuntos (A∩B)=0

P(AuB)=P(A) +P(B)-P(A∩B)
Como P(A∩B)=0 então temos:
P(AuB)=P(A) +P(B)
Exercícios de aplicação
a)A probabilidade de um aluno saber matemática quando se dedica é de 0,8 qual é a probabilidade de ele não saber calculo quando se dedica?
P(A)=0,8
P(Ᾱ)=?
P(A)=1-P(Ᾱ)
P(Ᾱ)=1-P(A)
P(Ᾱ)=1-0,8
P(Ᾱ)=0,2
R: A probabilidade de ele não saber calculo quando se dedica é de 0,2.
b)A probabilidade de um aluno ir a biblioteca em vinte anos é de 0,56 qual é a probabilidade de ela não ir a biblioteca nesse período?
P(A)=0,56
P(Ᾱ)=?
P(Ᾱ)=1-P(A)
P(Ᾱ)=1-0,56
P(Ᾱ)=0,34
R: A probabilidade de ir a biblioteca nesse período é de 0,34.
c)Sabendo que P(A)=0,6 e P(B)=0,15 e que P(A∩B)=0,3 calcule P(AuB)
P(AuB)=P(A) +P(B)-P(A∩B)
P(AuB)=0,6 +0,15-0,3
P(AuB)=0,45
R: A probabilidade de A união com B é de 0,45.
d)Sabendo que P(A)=0,25 e que P(AuB)=0,75 calcule a probabilidade de B P(B) sabendo que A e B são acontecimentos disjuntos
P(AuB)=P(A) +P(B)-P(A∩B)
P(AuB)=P(A) +P(B)
P(B)=P(AuB)-P(A)
P(B)=0,75 -0,25
P(B)=0,50
R: A probabilidade de B é de 0,50.
Exercício para praticar
1.Quantas faces tem um dado?
2. Laça-se dois dados para o ar qual a probabilidade de ter-se faces com os mesmos numero?
3. Laça-se duas moedas qual a probabilidade de termos duas caras?
4.Numa urna com bolas enumeradas de 1 a 90 qual a probabilidade de se extrair uma bola com enumeração maior que 69?