Regime de ressonância
Um circuito eléctrico de corrente alternada esta em regime de ressonância de a impedância equivalente conter apenas a parte resistiva (não conter parte indutiva nem parte capacitiva).
Ressonância circuito em serie
A impedância do circuito e dado por ;
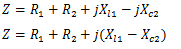
Dissemos que o circuito esta em ressonância se a impedância for totalmente resistiva.
Ou seja
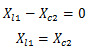
Ressonância circuito em paralelo
A impedância do circuito e dado por ;
A impedância equivalente não terá parte capacitiva nem indutiva (estará em ressonância) se;
Exemplo de aplicação
1.Uma bobina real (com resistência e indutância) e um condensador ideal estão ligados em série. No regime de ressonância a tensão nos terminais do capacitor é de 180 V. Determine a tensão nos terminais da bobina. Considere que a tensão de alimentação vale 90 V.
Resolução
Como a bobina é real (com resistência e indutância) terá logicamente uma tensão na resistência (URB )e outra na indutância (ULB) ou seja;
A tensão n0s terminais da bobina e dada por UB =URB+jULB
Vamos determinar a tensão ULb como o circuito esta em regime de ressonância XL=Xc e como o capacitor e o indutor estão em serie a corrente também é a mesma. Dai como a tensão e a corrente e a mesma a tensão também será a mesma ULB=Uc=180V
A tensão total do circuito é dado por ;
U=URB+ULb-Uc
URB =U-ULB+Uc
URB=90-180+180
URB =90V
Agora podemos substituir ULB=180V ; URB =90V na expressão para calcular a tensão nos terminais da bobina
UB= URB +jULB
UB =90+j180
UB =201,25V
Valores instantâneos
1. Calcular os valores instantâneos das correntes do circuito da figura dada.
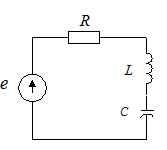
Resolução
Vamos separar a tensão em 3 instante.
A corrente do circuito será a soma da corrente nos 3 instantes
Passo I
Vamos calcular I1 com E=15V
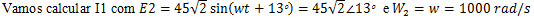
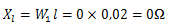
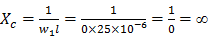
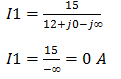
Passo II
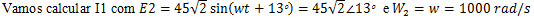
Passo III
Finalmente tendo as três correntes
A corrente em função do tempo será dado por;
Indutância Mútua
1.Calcular as correntes do circuito que se segue aplicando o método de malhas independentes. E1 = 10V ; XL1 = 5Ω ; XC2 = 5Ω ; XL3 = 5Ω ; R2 = 2Ω ; XM = 2Ω . Resoluçã…
Malhas independentes( Circuitos de corrente continua)
Malhas independentes Passos para a resolução de exercícios usando o medo de malhas independentes 1°-Definir para cada malha o nome e sentido da corrente; 2°-Aplicar a segunda lei de Kirchoff para obte…
Aplicação do método de Malhas independentes em circuitos de corrente alternada (CA).
A aplicação do método de Malhas independentes para a resolução de em circuitos de corrente alternada (CA) é de forma análogo que para circuitos de corrente continua. O que muda é que em corrente alter…
Método de sobreposição
Método de sobreposição O método de sobreposição consiste em analisar o circuito parcialmente; Analisando o circuito com apenas uma fonte de cada vez. Para isso devemos eliminar as fontes deixando apen…
Regime de ressonância e valores instantâneos
Regime de ressonância Um circuito eléctrico de corrente alternada esta em regime de ressonância de a impedância equivalente conter apenas a parte resistiva (não conter parte indutiva nem parte capacit…