1.Dois números distam entre sim 5 unidades, sendo um deles 3. A tradução da afirmação anterior em linguagem matemática é;
A. 5-3 B. 3-5 C. |x-5|=3 D. |3-x|=5 E. |3+x|=5
Resolução
A distancia entre dois números e dado por |y-x|=d
Segundo o enunciado d=5 e um deles é 3 (y=3)
|y-x|=d
|3-x|=5
Resposta. D
2. Na figura ao lado esta representada a preto a solução da inequação;

A. |x-3|<1 B. |3-x|>1 C. |x+3|<7 D. |x+3|≤ 7 E. |x-3|≤1
Resolução
Como as bolinhas na solução são pitadas significa que a inequação dever ser de ≤ ou ≥ so pode ser alternativa D ou E para saber qual e a alternativa entre elas a correcta vamos resolver as inequações
D.|x+3|≤ 7
x+3≤ 7 e x+3≥-7
x≤ 7-3 e x≥-7-3
x≤ 4 e x≥-10
-10≤x≤4
Essa não é correcta
Agora vamos resolver ;
E. |x-3|≤ 1
x-3≤ 1 e x-3≥-1
x≤ 1+3 e x≥-1+3
x≤ 4 e x≥2
2≤x≤4
Essa é correcta
Resposta. E
3. Na equipe de futebol de são do bairro militam 10 jogadores. Pretende-se escalar o grupo que vai jogar na semana seguinte, tendo em conta que o Cossa e o Rafique devem obrigatoriamente dos cinco seleccionados Quantas possibilidades existem? Nota; num jogo uma equipe de futebol de salão é constituída por 5 jogadores.

Resolução
Como o Cossa e o Rafique devem obrigatoriamente vamos separar eles dos 10 assim ficamos com 8 pessoas e passamos a queres 3
Assim nos ficamos com 8, assim nos temos Cossa e o Rafique queremos eles os dois .

e → multiplicação
ou → Adição
Resposta. C
4. Uma roleta mostra os números de 1 a 8 , a probabilidade de acertar um numero menor do que 3 é ;

Resolução

De 1 a 8 temos 3 números menores que 3 então cf=2
De 1 a 8 temos 8 números então cp=8

Resposta. B
Responda as questões 5, 6, 7 relacionadas com a figura ao lado

5. A circunferência de centro O. Circunscrita no triângulo ABC tem perímetro 18,84cm. Os segmentos OB e CD são perpendiculares e tem a mesma medida. A área do triângulo é;

Resolução

Na figura podemos ver que B=AB=D=2R e h=CD=OB=R

Para encontrar o valor do raio vamos usar o perímetro
P=2πR

Agora com o valor do raio encontrado vamos voltar para equação que encontramos para calcular a área do triângulo

Resposta. B
6. A medida dos segmentos DB e DA estão porção de 1 para 3. A medida de DB em cm, é igual a;

Resolução


A figura mostra que DB é a metade do raio
Resposta. C
7. PASSE PARA A PERGUTA SEGUINTE
8. Ao lado esta representado uma sequência de figuras, metendo se essa lei de formação o numero de quadradinho da figura na posição 7 é;
A. 35 B. 30 C. 21 D. 36 E. 28
Resolução
Número de quadradinho na posição 1; 1
Número de quadradinho na posição 2; 1+2
Número de quadradinho na posição 3; 1+2+3
Número de quadradinho na posição 4; 1+2+3+4
Número de quadradinho na posição 5; 1+2+3+4+5
Número de quadradinho na posição 6; 1+2+3+4+5+6
Número de quadradinho na posição 7; 1+2+3+4+5+6+7=28
Resposta. E
9. Dados preposições p e q a negação de p˄~q
A. ~p˄~q B. ~p˄q C. ~p˅~q D. ~p˅q E. p˅q
Resolução
~(p˄~q)
~p˄~(~q)
~p˄q
Resposta. B
10. Dados as preposições t; chove e r; vou a praia s; não chove então vou a praia e traduzida simbolicamente por;
A. ~t↔r B. ~t˄r C. ~t˅r D. t→~r E. ~t→r
Resolução
s; não chove então vou a praia
não chove então ; ~t
então; →
vou a praia; r
Traduz numa só como; ~t↔r
Resposta. A

Resolução

Resposta. E

Resolução

Resposta. A

Resolução

Resposta. B;

A. -1 B. 1 C. 0 D. 2 E. -2
Resolução
Como x=2 é raiz do polinómio significa que P(2)=0

Resposta. B;
Com base no gráfico responda as questões 15 a 20

15. A deriva da função no ponto x = 0 é igual a:

Resolução

Resposta. C;
16. A solução da equação f(x)-g(x)=0 é;
A. x=2 B. x=3 C. x=0 D. x=-3 E. x=-2
Resolução
f(x)-g(x)=0
f(x)=g(x)
os gráficos são iguais (intersectam-se no ponto x=0)
Resposta. B;
17. Para f(x)=3 o valor de x é;
A. 0 B. 1,5 C. 2 D. 0 ou 1,5 E. 0 ou -2
Resolução
f(x)=3 no ponto x=0
Resposta. B
18. A expressão analítica da função é;

Resolução
A expressão analítica e dada por f(x)= mx+b

Para calcular o valo de b vamos se basear no gráfico onde podemos observar que quando y=3 x=0 (f(0)=3)

b=3

Resposta. D
19. h(x)≤3 se;
A. xє]0;1,5[ B. xє[0;1,5[ C. xє]0;1,5] D. xє[0;1,5] E. Nenhuma das alternativas anteriores
Resolução
h(x)≤3 queremos onde h(x) esta em baixo de 3 no gráfico notamos que e de 0 a 1,5 e como é ≤ os intervalos são fechados
Resposta. D
20. Os valores que satisfazem a inequação f(x)<h(x) são;

Resolução
f(x)<h(x) queremos onde f(x) esta em baixo em relação a h(x) 3 no gráfico notamos que para todos valores f(x) esta em baixo em relação a h(x) excepto no x=0
xє R\{0}
Resposta. C;

A. g(k+1) B. g(k) C. g(k-1) D. 1 E. g(2k+1)
Resolução

Resposta. B

Resolução

Nota; πk é o período da função tgx
Resposta. Nenhuma das alternativas;

Resolução
Vamos primeiro calcular y’
y=e2x
y’=2e2x
Vamos substituir essa expressão de y’ na equação

Resposta. A
24. Uma Barra de ferro foi feita retirada o lume, tendo atingido a temperatura ambiente passando algumas horas, conforme o gráfico ao lado. É incorrecto dizer que;

A. A temperatura no momento em que se retirou a barra era de 70ᵒ
B. A variação da temperatura foi constante
C. A temperatura diminui constantemente
D. A temperatura ambiente era de 20ᵒ
É incorrecto afirmar que A variação da temperatura foi constante, pois se a variação da temperatura tivesse sido constante o gráfico seria uma linha recta.
Resposta. B
25. O produto (2+ki)(2+i) é um numero imaginário para k igual a;
A. k = – 1 B. k = 1 C. k = 4 D. k = – 4 E. k = – 3
Resolução
(2+ki)(2+i)
4+2i+2ki-k
4-k+(2+2k)i
O número será imaginário se a parte imaginária for diferente de zero
2+2k≠0
2k≠ – 2
k≠ – 2/2
k≠ – 1
O numero será imaginário se k≠ -1
Resposta. Nenhuma das alternativas

Resolução

27. Das funções seguintes qual aquela cuja primitiva é igual a própria função

Resposta. D


Agora vamos resolver a inequação




A. 16 B. -16 C. -12 D. 12 E. 9
Resolução

31. A distância entre A(2,3) e B(-2,-2) é

Resolução

Resposta. D

33. Em relação ao gráfico aprestado, é falso afirmar que;
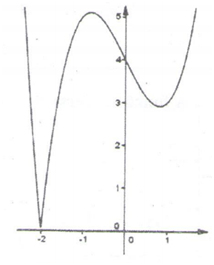
A. A função é decrescente em ]- ∞ ,-2[U]-1,1[
B. A função tem um ponto de inflexão em x=0
C. A derivada da função é nula em x=-2 , x= – 1 e x=1
D. Em ]-2,1[ a segunda derivada é negativa
E. A função admite um máximo relativo em x= -1
Resolução
É falso afirmar que a derivada da função é nula em x=-2 , x= – 1 e x=1, pois em x= – 1 a derivada da função é não nula. (em x= -1 nos carregamos a parte negativa para cima pois a função em modular)
Resposta. C
34. A expressão analítica da função representa na figura ao lado é;

Resolução
Toda função esta no lado positivo isso significa que toda a função esta dentro do modulo
Então a resposta correcta é C ou D
Para saber qual delas é correcta vamos observar o gráfico e notaremos que quando y=0 x=-2 aqui satisfazer essa condição será à correcta

35. PASSE PARA A PERGUNTA SEGUINTE.

Resposta: A



Resposta: Nenhuma das alternativas



Resolução
É falso afirmar que a função tem limite em x = 2 pois como os limites laterais em x = 2 são diferentes então não existe limite nesse ponto.
Resposta. C


Resposta C

Na figura abaixo esta representado o gráfico da função y=f(x). Com base no gráfico responda as questões 44 e 45.






6,5 não é numero natural pois n deve ser natural.
Resposta. A



Em relação ao gráfico da função y=h(x) representado em baixo responda as questões 52 a 56.

52. A função inversa de y=h(x) é:


Resolução
h(0) não existe pois x=0 não faz parte do domínio.
Resposta. E
56. É falso a afirmação que y=h(x) ;
A. É descontínua com salto de 2ª espécie em x=0
B. Admite derivada em x ε R\ (0)
C. É simétrica em relação a origem
D. A função não é injectiva
E. h(x)=h(-x)
Resolução
É falso afirmação que a função não é injectiva.
Pois a função é injectiva (é injectiva porque trancando rectas paralelas ao eixo elas toucam a função em um e único ponto.)
Resposta. D
A função é descontínua eliminável (porque os limites laterais são iguais e são de diferentes do valor da função no ponto -3)

Resposta. D
Veja mais conteúdo sobre os exames de admissão
Edital de Exames para Admissão aos Institutos Técnicos Profissionais – Ano Lectivo 2025
Edital de Exames para Admissão aos Institutos Técnicos Profissionais – Ano Lectivo 2025. Já es…
Edital ISCISA 2025 em pdf
Edital de exames de admissão ao ISCISA 2025 O edital de exames de admissão ao Instituto superior de …
Edital ISCISA 2025
Edital de exames de admissão ao ISCISA 2025 O edital de exames de admissão ao Instituto superior de …
Edital UniRovuma 2025
Já esta disponível o Edital de Exames de Admissão a Universidade Rovuma 2025 O Edital de exames de a…
Edital Universidade Púnguè 2025
Já esta disponível o Edital de Exames de Admissão a Universidade Edital Universidade Púnguè 2025 O E…
Edital Universidade Licungo 2025
Já esta disponível o Edital de Exames de Admissão a Universidade Licungo 2025 O Edital de exames de …






