Progressão geométrica é um tipo de sucessão em que a razão entre os termos consecutivos é constante.
Exemplo de progressão geométrica.
Ex1: an = (2,4,8,16,32…)
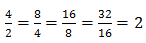
Conforme vermos a razão entre os termos consecutivos é constante.
Ex2; vn = (25,125,625,3125 …)

Conforme vermos a razão entre os termos consecutivos é constante.
Mais exemplos de progressão geométrica
Ex3; in = (2,6,18,54,162…) a razão é 3 (r=3)
Ex4; un = (1,10,100,1000,1000 …) a razão é 10 (r=10)

Exercidos de aplicação
1.Sabendo que a sequência 3, a2 , 75 é uma progressão geométrica crescente determine o valor de a2,
Resolução
Como a é uma progressão geométrica a razão entre os termos consecutivos será constante ou seja;

Termo geral de uma progressão geométrica
Em geram uma sucessão é dada na forma an = (a1, a2, a3, a4 …)
Como a sucessão e uma PG então

Então na PG
a1 = a1
a2= a1 • r
a3= a1 • r2
a4= a1 • r3
a5= a1 • r4
an= a1 • r(n-1)
Conforme vimos o termo geral de uma progressão geométrica é;
an= a1 • r(n-1)
Exercício de aplicação
2. Dada a progressão an = (6, 18,54,162…) Determine;
a) O termo geral sucessão
b) O sétimo termo da sucessão?
Resolução
a)Para determinar o termo geral sucessão usaremos a forma to termo geral que vimos anteriormente
an= a1 • r(n-1)
Podemos ver na sucessão que ;
a1=6 e r=3
Então o termo geral da sucessão é ;
an= 6 • 3(n-1)
b) O sétimo termo da sucessão é obtido pela forma do termo geral
an= 6 • 3(n-1)
a7= 6 • 3(7-1)
a7= 6 • 36
a7= 6 • 729
a7=4374
3. Numa progressão geométrica sabe se que a5=64 e que a8=512
a) Qual é o termo geral sucessão dessa progressão
b) Qual é o décimo quinto termo dessa progressão geométrica?
Resolução
a)A partir da forma do termo geral de uma (PG) que é an= a1 • r(n-1)
a5= a1 • r(5-1) e a8= a1 • r(8-1)
a5= a1 • r4e a8= a1 • r7
Fazendo a razão entres esses termos temos;

Agora vamos calcular a1

Substituindo a1 e r na forma do termo geral da (PG) temos;
an= a1 • r(n-1)
an= 4 • 2(n-1)
an= 22 • 2(n-1)
an= 2(2+n-1)
an=2(n+1)
R: o termo geral da sucessão é an=2(n+1)
b) Para determinar o décimo quinto termo vamos substituir “n” por 15;
an=2(n+1)
a15=2(15+1)
a15=216
R: O décimo quinto da progressão é 216
Propriedade de uma progressão geométrica
an = (5,10,20,40,…,80,160,320,640)
5 • 640=10 • 320= 20 • 160= 40 • 80
Numa progressão geométrica produto dos termos equidistantes é igual.
a1 • an=a2 • a(n-1)= a2 • a(n-1)= a3 • a(n-2)= a4 • a(n-4)=…
Soma dor termos de uma progressão geométrica
an = (a1, a2, a3, a4 … a(n-4), a(n-3, a(n-2), a(n-1), an)
sn = a1+ a2+ a3+ a4 … a(n-4) + a(n-3) + a(n-2) + a(n-1) + an
Multiplicando ambos membros pela razão r temos;
sn r= a2+ a3+ a4 … a(n-4) + a(n-3) + a(n-2) + a(n-1) + a(n+!)
sn = a1+ a2+ a3+ a4 … a(n-4) + a(n-3) + a(n-2) + a(n-1) + an
sn r- sn = a1 • rn -a1
sn (r- 1) = a1(rn – 1)
sn (r- 1) = a1(rn – 1)

A soma dos termos de uma progressão geométrica é;

Exercícios de aplicação
4. Dada a sucessão an = (2,6,12,24…)
a) Qual é o termo geral sucessão
b)Calcule o sexto termo da sucessão
c)Calcule a soma dos 10 primeiros termos da sucessão
Resolução
a)Para determinar o termo geral sucessão usaremos a forma to termo geral que vimos anteriormente
an= a1 • r(n-1)
Podemos ver na sucessão an = (2,6,12,24…) que ;
a1=2 e d=3
Então o termo geral da sucessão é ;
an= a1 • r(n-1)
an= 2• 3(n-1)
b)O sexto termo da sucessão é pode ser calculado apartar de;
a6= 2• 3(6-1)
a6= 2• 35
a6= 2•243
a6= 486
b)A soma dos 12 primeiros termos da sucessão é dada pela forma;

Soma dos infinitésimos termos de uma progressão geométrica

Exercício de aplicação


Fracção geratriz
Fracção geratriz é uma fracção capaz de expressar um número decimal com dízimas periódicas.

Exemplos de aplicação
Ex2; Escreve o número 2.333333…sobre forma de fracção
Resolução
2+0.333333…=2+0.3+0,03+0,003+0,0003+0,00003…
Note que (0.3+0,03+0,003+0,0003+0,00003…) a partir de 0,3 ate ao infinito temos um P(G) com a1=1e r=0,1


Ex2; Escreve o número 4.121212…sobre forma de fracção
Resolução
4+0. 121212…=4+0.12+0,0012+0,0000012…
Note que (0.12+0,0012+0,0000012…) a partir de 0,12 ate ao infinito temos um P(G) com a1=0,12e r=0,01

Aprender também:Progressão aritmética (PA)
Factorial de um número e permutações
Aplicação da primeira e segunda derivada extremos e ponto de infecção