Limites indeterminações do tipo zero sobre zero

Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a variável pela sua tende temos uma “expressão” do tipo zero sobre zero (0/0).

Como resolver limites contendo indeterminações do tipo zero sobre zero?

Para resolver esse tipo de limites (Limites com indeterminações do tipo zero sobre zero) geralmente procuramos uma forma de eliminar (simplificar) a expressão que cria a indeterminação para a fazer esta simplificação na maioria dos casos a gente factoriza usando diversas técnicas como por exemplo calcular os zeros, binómio de Newton etc …

Cálculo de limites envolvendo indeterminações do tipo zero sobre zero

Exercício #1

Resolução do exercício #1 limites zero sobre zero

Primeiro vamos substituir onde vem x pela tendência que é zero

Temos uma indeterminação do tipo zero sobre zero, para resolver este limites vamos evidenciar o x no numerador e no denominador de seguida iremos simplificar e depois de simplificar vamos substituir x pela tendência que é zero

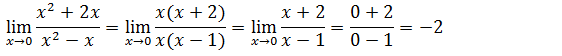
Exercício #2

Resolução do exercício #2 limites zero sobre zero

Vamos substituir onde vem x pela tendência

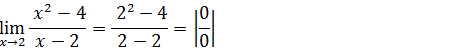
Temos uma indeterminação do tipo zero sobre zero, e no numerador temos uma diferença de quadrados pois “x²-4= x²- 2²=(x-2)(x+2)” vamos aplicar esse princípio de seguida iremos simplificar e depois de simplificar vamos substituir x pela tendência que é zero

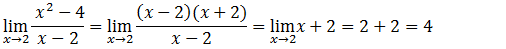
Exercício #3

Resolução do exercício #3 limites zero sobre zero

Primeiro vamos substituir onde vem x pela tendência

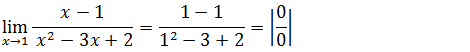
Vamos factorizar a expressão colocando na forma a(x-x1)(x-x2) onde a=1 , x1=2 e x2=2 x²-3x+2=(x-1)(x-2) e pois de factorizar vamos colocar a mesma na expressão do limite e simplificar.

Exercício #4

Resolução do exercício #4 limites zero sobre zero

Vamos substituir onde vem x pela tendência

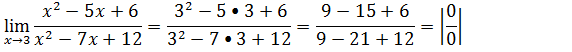
Vamos factorizar as duas expressões e colocando as na forma a(x-x1)(x-x2) onde para o numerador a=1 , x1=3 e x2=2  então fica x²-5x+6=(x-3)(x-2) , e para o denominador a=1 , x1=3 e x2=4  então fica x²-7x+12=(x-3)(x-4) tendo as duas expressões já factorizadas vamos fazer a simplificação depôs substituir por 3 que é a tendência.

Limites recorrendo ao par conjugado

Recorrer ao par conjugado tem sido uma técnica muito usado no calculo de limites sobre tudo nos limites onde a variável esta raiz e limites trigonométricos.
Exercício #5

Resolução do exercício #5 limites zero sobre zero

Vamos substituir onde vem x pela tendência

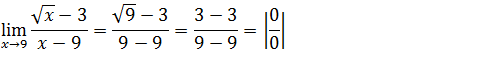
Temos uma indeterminação do tipo zero sobre zero 0/0 para resolver este limite (para levantar a indeterminação) devemos recorrer ao par conjugado da expressão que conte a raiz (do numerador)

Exercício #6

Resolução do exercício #6 limites zero sobre zero

Vamos substituir onde vem x pela tendência

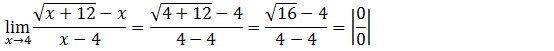
Para a resolução desse limite será feita de igual modo ao limite anterior recorreremos ao par conjugado

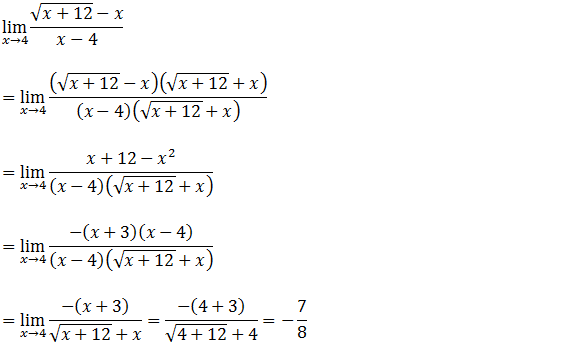
Limites usando mudança de variável

Para o cálculo de limites muitas vezes é necessário recorrer a diversão método sendo a mudança de variável o meto mais usado veremos agora como ele é usando no calculo de limites com indeterminações 0/0
Exercício #7

Resolução do exercício #7 limites zero sobre zero

Vamos substituir onde vem x pela tendência

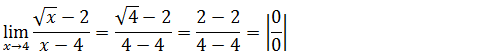
Para eliminar a raiz usaremos mudança de variável iremos substituir x por uma variável ao quadrado,para eliminar a raiz. 

Seja x=t² ; t→ √x=√4=2 

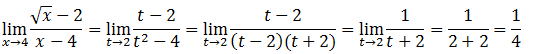
Exercício #8

Resolução do exercício #8 limites zero sobre zero

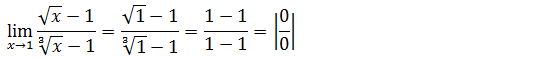
Vamos substituir a variável x por uma outra variável, que nos permita eliminar as raízes em simultâneo, para isso vamos o índice das raízes uma é raiz quadrática ( índice dois) e a outra e raiz cúbica (índice três ) vamos calcular o m.m.c dois índices ( m.m.c de 2 e 3 ) que é seis então substituiremos x por uma variável qualquer elevado a seis para poder eliminar as duas raízes em simultâneo

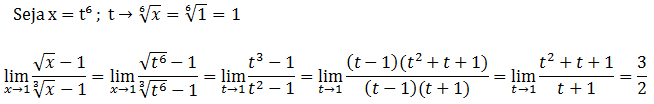
Usando método de Bioti Roffini

O método de Bioti Roffin é usado no calculo de limites para poder fazer a factorizarão quando temos polinómios com grão superior a dois.

Exercício #9

Resolução do exercício #9 limites zero sobre zero

Vamos substituir onde vem x pela tendência

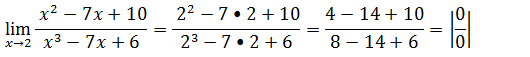
vamos factorizar x²-7x+10

	1	-7	10
2		2	-10
	1	-5	0

x²-7x+10=(x-1)(x-5)

vamos factorizar também x³-7x+6 mais primeiro vamos completar a expressão x³-7x+6=x³+0x²-7x+6

	1	0	-7	6
2		2	4	-6
	1	2	-3	0

x³-7x+6=(x-1)( x²+2x-3)

Tendo já as duas expressões factorizadas vamos substituir na expressão do limite e simplificar

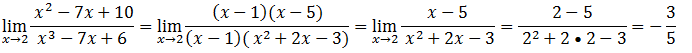
Exercício #10

Resolução do exercício #10 limites zero sobre zero

Vamos substituir onde vem x pela tendência

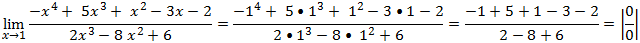
vamos factorizar primeiramente o numerador -x⁴+5x³+x²-3x-2

	-1	5	1	-3	-2
1		-1	4	5	2
	-1	4	5	2	0

-x⁴+5x³+x²-3x-2=(x-1)(-x³+4x²+5x+2)

vamos factorizar também x³- 8x²+6 mais primeiro vamos completar a expressão x³- 8x²+6= x³- 8x²+0x+6

	2	-8	0	6
1		2	-6	-6
	2	-6	-6	0

x³- 8x²+6=(x-1)(2x²-6x-6)

Agora que já factorizamos podemos calcular o nosso limite basta simplificar

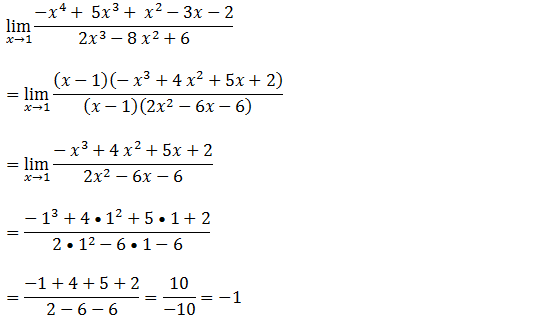
Exercícios de limites indeterminações zero sobre zero para praticar

Usamos os conhecimentos adquiridos a partir dessa aula e das aulas anteriores de calcule os seguintes limites:

Veja mais uma das nossa aulas

---