Derivada de uma função usando definição

Definição de derivadas

Chamamos de derivada da função f(x) no ponto qualquer a inclinação da recta tangente ao gráfico da função f(x) nesse ponto, e representamos por f'(x).

O que é uma recta tangente ao gráfico de f(x) ?

Recta tangente é uma recta que intercepta a função f(x) em um único ponto.

Vamos representar geometricamente a derivada de uma função e fazer a interpretação.

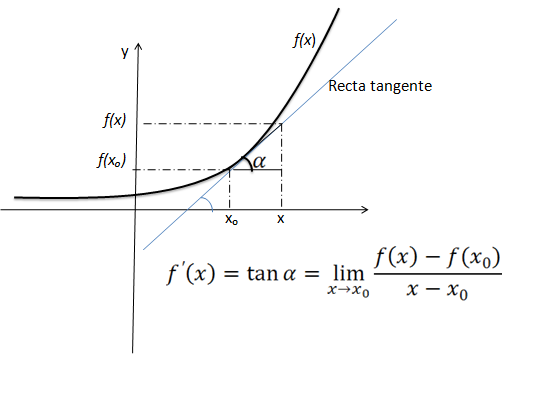
Definição de derivada em um no ponto x=xₒ

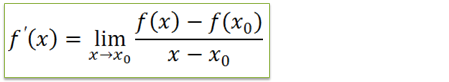
1. Exercícios cálculo de derivadas usando a definição derivada;

a) Ache a derivada da função f(x)=x²-3x usando a definição de derivada

Para calcular a deriva dessa função usaremos a definição da derivada usando limites

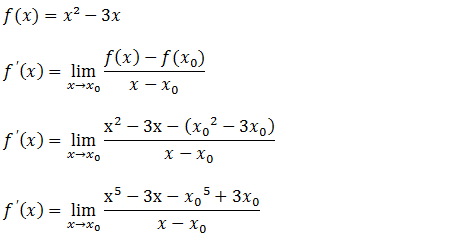
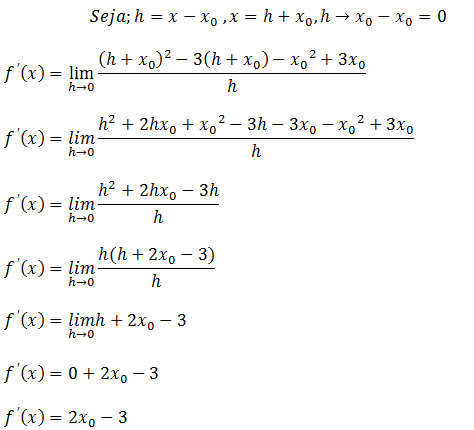
Para facilitar a resolução de derivadas usando a definição, para não ter que perder tempo fazendo mudança de variável ao calcular o limite na resolução das derivadas usando a definição, vamos fazer a mudança de variável logo na fórmula da definição da derivada.

Ao resolver derivadas usando a definição já nessa formula ira nos facilitar pois não iremos mais ter que mudar a variável para calcular o limite.

b)Encontre a derivada da função f(x)=2x²+5x-1 usando a definição de derivada

Para facilitar o cálculo dessa derivada usando a definição de derivada usaremos a fórmula da definição da derivada mais simplifica que é;

c) Calcule a derivada da função f(x)= 3x-2 usando a definição de derivada

De formula análogo para calcular a derivada da função f(x)= 3x-2 usaremos a formula da definição de derivada;

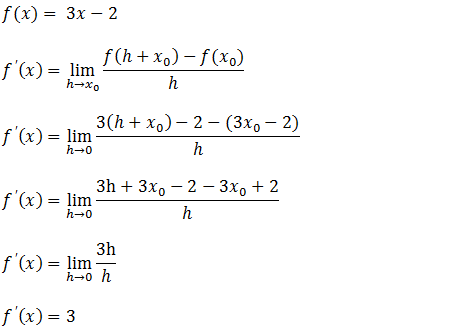
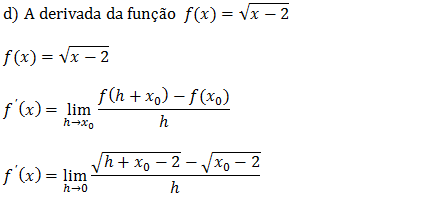
Como demos raiz para resolver este limite vamos recorrendo ao par conjugado (multiplicar o numerador e denominador pelo par conjugado da expressão no numerador); 

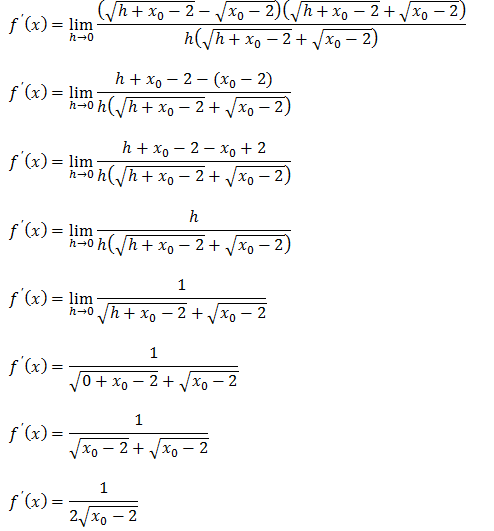
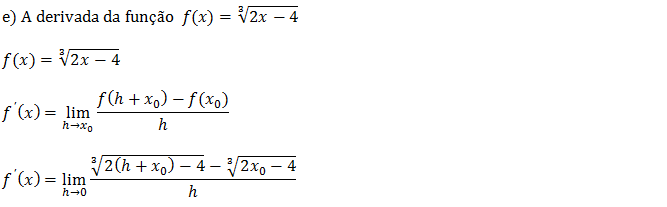
Depois de aplicar a definição de derivada chegamos a uma expressão de limites com raiz cúbica para resolver vamos usar a técnica de multiplicar pelo par conjugado

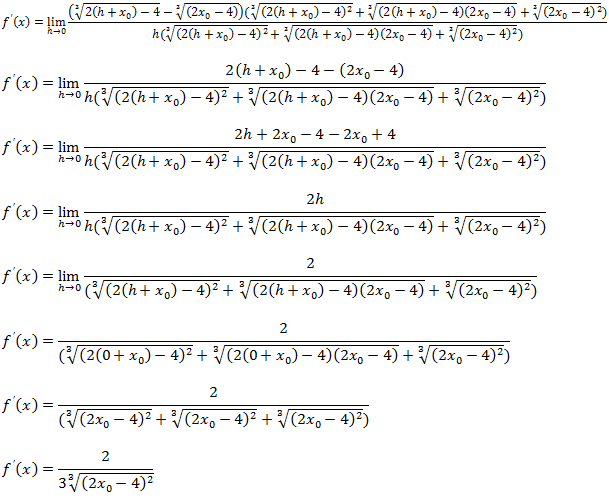
A fórmula que nos vimos acima permite-nos calcular a deriva de uma função em um ponto x=xₒ. Para calcular a derivada de uma função usaremos a mesma fórmula porem não será em um ponto x=xₒ mais sim em um ponto x=x seja;

Representação de derivada de uma função

As quatro formas mais usados para representar a derivada de uma função são;

“Durante os nossos estudos de derivadas usaremos mais as três primeiras representações.”

Exercícios para praticar sobre derivada de uma função usando a definição de derivada usando limites.

Usando a definição de derivada calculo a derivadas da funções;

---

Aprenda mais sobre as derivadas