Limites laterais (Limite lateral à esquerda e limite lateral à direita)

Seja dado uma função f(x) cujo o gráfico é representado na figura abaixo:

Como achar os limites laterais e o que são limites laterais?

Para chegarmos ao ponto da abcissa x=a podemos usar dois caminhos (podemos se aproximar do ponto “a”  do lado direito ou pelo lado esquerdo) a esses caminhos ao qual se aproximamos da abcissa x=a chamaremos de limites laterais e representaremos por;

Limite lateral a esquerda

Limite lateral a direita

Limite lateral nos gráficos

Para indicar os limites laterais de uma função em um determinado ponto do gráfico basta apenas observar a o gráfico da função em questão e se aproximamos no ponto do lado direito ou esquerdo (esquerdo para o limite lateral a esquerda e direito para o limite lateral a direita) e vemos o valor na qual a função se aproxima esses valor é o limite lateral nesse ponto.

Exercícios de limites laterais

1.Dada o gráfico abaixo determine os limites laterais no ponto x=2

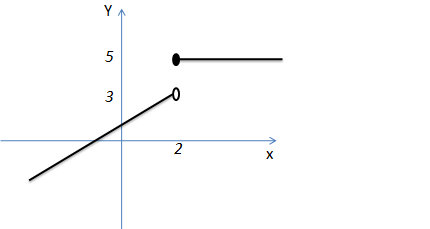
Resolução

*Se aproximado de 2 pela esquerda a nossa função tende a 3 então diremos que o limite lateral a esquerda da nossa função é 3.

*Se aproximado de 2 pela direita a nossa função tende a 5 então diremos que o limite lateral a direita da nossa função é 5.

2.Dada o gráfico abaixo determine os limites laterais no ponto x=-1

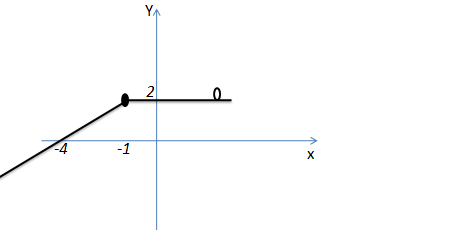
Resolução

*Se aproximado de -1 pela esquerda a nossa função tende a 2 então diremos que o limite lateral a esquerda de um para nossa função é 2.

*Se aproximado de 1 pela direita a nossa função tende a 2 então diremos que o limite lateral a direita da nossa função é 2.

3.Dada o gráfico abaixo determine os limites laterais no ponto x=3

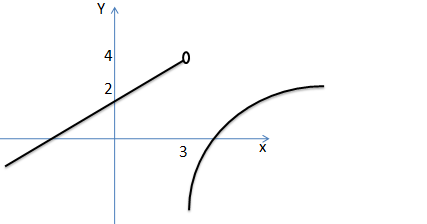
Resolução

*Se aproximado de 3 pela esquerda a nossa função tende a 4 então diremos que o limite lateral a esquerda da nossa função é 4.

*Se aproximado de 3 pela direita a nossa função tende a -∞ então diremos que o limite lateral a direita da nossa função é -∞.

4.Dada o gráfico abaixo determine os limites laterais no ponto x=1

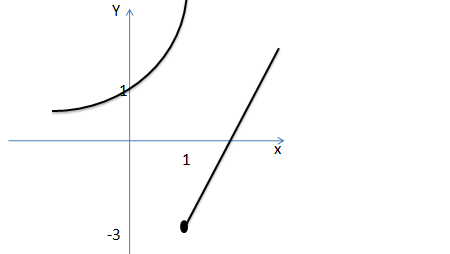
Resolução

*Se aproximado de 1 pela esquerda a nossa função tende a +∞ então diremos que o limite lateral a esquerda da nossa função é +∞.

*Se aproximado de 1 pela direita a nossa função tende a -3 então diremos que o limite lateral a direita da nossa função é -3.

5.Dada o gráfico abaixo determine os limites laterais no ponto x=5

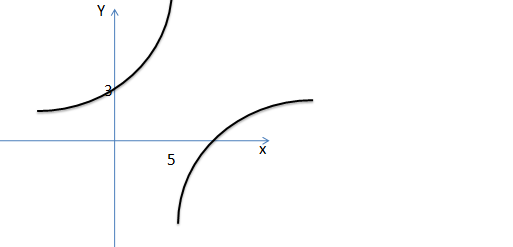
Resolução

*Se aproximado de 5 pela esquerda a nossa função tende a +∞ então diremos que o limite lateral a esquerda da nossa função é +∞.

*Se aproximado de 5 pela direita a nossa função tende a -∞ então diremos que o limite lateral a direita da nossa função é -∞.

Limite lateral para função dada em forma de intervalo

Uma função poder ser aprestado em forma de dois mais intervalos nesses casos também é possível encontrar os limites laterais para isso temos que saber indicar o intervalo que compreende o lado direito (para calcular o limite lateral a direita) e o intervalo que conte o lado esquerdo (para calcular o limite lateral a esquerda)

1.Determine os limites laterais para a função f(x) no ponto x=0

Resolução

Primeiro calcularemos o limite lateral a esquerda, Para isso devemos saber que o lado esquerdo do três são números menores que três. Então para o limite lateral a esquerda usaremos a parte de menor ou igual

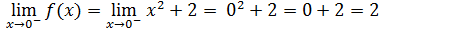
De seguida calcularemos o limite lateral a direita, Para isso devemos saber que o lado direito do zero são números maiores que zero. Então para o limite lateral a esquerda usaremos a parte de maior.

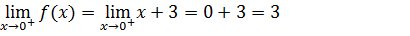
2.Calcule os limites laterais para a função f(x)no ponto x=2

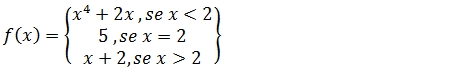
Primeiro calcularemos o limite lateral a esquerda, Para isso devemos saber que o lado esquerdo do dois são números menores que dois. Então para o limite lateral a esquerda usaremos a parte de menor ou igual

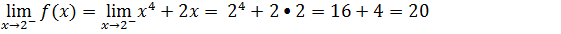
De seguida calcularemos o limite lateral a direita, Para isso devemos saber que o lado direito do dois são números maiores que dois. Então para o limite lateral a esquerda usaremos a parte  com a condição de maior.

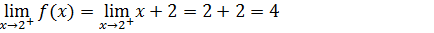
3.Determine os limites laterais para a função f(x)no ponto x=4

Vamos primeiro a analisar a expressão modular que esta no numerador, uma expressão modular pode ser escrita em duas condições, para o caso da nossa podemos escrever como sendo;

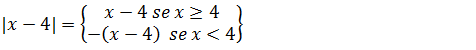
A expressão do módulo resulta em duas condições vamos substituir essas condições na nossa função principal.

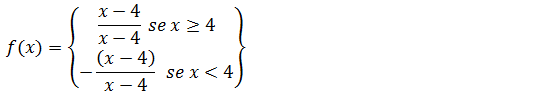
Agora podemos facilmente calcular os limites laterais

Para calcular esse limite lateral vamos usar a parte da função com a condição menor que quatro pois é essa parte da função que esta do lado esquerdo do quatro.

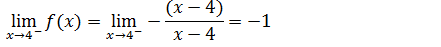
De seguida calcularemos o limite lateral a direita

Para calcular esse limite lateral vamos usar a parte da função com a condição maior ou igual a quatro pois é essa parte da função que esta do lado direito de quatro.

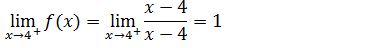
4.Determine os limites laterais para a função f(x)no ponto x=0

Primeiro calcularemos o limite lateral a esquerda de zero

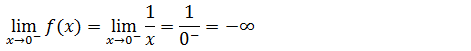
Nota; Zero a esquerda corresponde a valores próximos de zero mais do lado negativo, pois isso temos menos infinito.

De seguida calcularemos o limite lateral a direita do zero

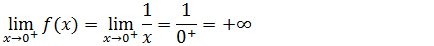
Nota; Zero a direita corresponde a valores próximos de zero mais do lado positivo, pois isso temos mais infinito.

5.Determine os limites laterais para a função f(x)no ponto x=2

Primeiro calcularemos o limite lateral a esquerda, Para isso devemos saber que o lado esquerdo do três são números menores que três. Então para o limite lateral a esquerda usaremos a parte de menor ou igual

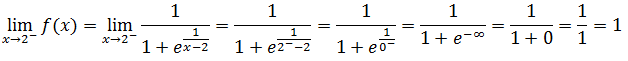
De seguida calcularemos o limite lateral a direita, Para isso devemos saber que o lado direito do zero são números maiores que zero. Então para o limite lateral a direita usaremos a parte de maior.

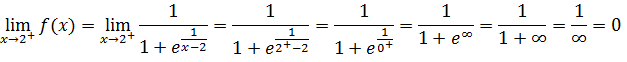
Exercícios para praticar limites laterais

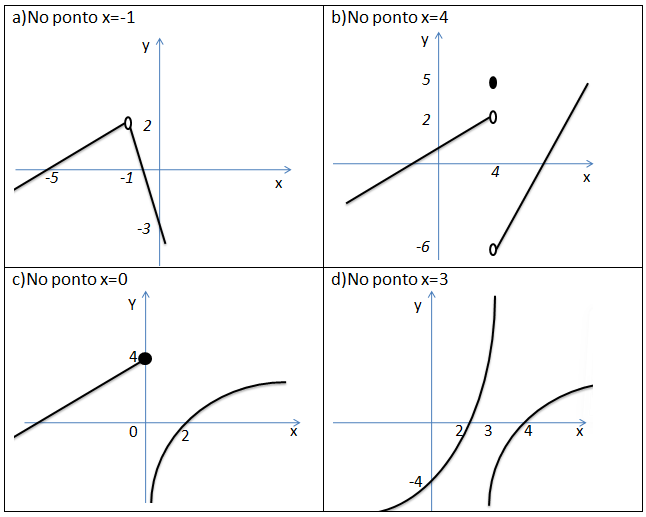
1.Para os gráficos a seguir indique os limites laterais no ponto da abcissa indicado

2.Calcule os limites laterais para os exercícios a seguir

Veja mais uma das nossa aulas