Resolução de Exames de Matemática Admissão UP 2018

1.Três camisas e cinco gravatas custam 4.600,00 Mt, duas camisas e três gravatas
custam 3.000,00 Mt. Cinco camisas e sete gravatas custam:

A. 6.900.00 Mt B. 7.400,00 Mt C. 8.200,00 Mt D. 9 100,00 Mt

Resolução : seja C- camisa, G- gravata

Três camisas e cinco gravatas custam 4.600,00 Mt matematicamente temos; 3C+5G=4600

Duas camisas e três gravatas custam 3.000,00 Mt matematicamente temos; 2C+3G=3000

Temos um sistema de duas incógnitas vamos resolver esse sistema assim teremos o preço de cada artigo

3C+5G=4600

2C+3G=3000

Vamos usar multiplicar por (2) na primeira equação e multiplicar por (-3) na segunda equação depois fazermos adição ordenada

6C+10G=9200

-6C-9G=-9000

¯¯¯¯¯¯¯¯¯¯¯¯

G=200

Usaremos a primeira equação para termos o valor de “C”

3C+5G=4600

G=200

3C+5•200=4600

3C=4600-1000

3C=3600

C=1200

Significa que cada gravata custa 200,00Mt e cada camisa custa 1200,00mt

Então Cinco camisas e sete gravatas custam 5 vezes o preço de uma camisa mais sente vezes o preço de um gravata

5C+7G=5•1200,00Mt+7•200,00Mt=6000,00Mt+1400,00Mt=7400,00Mt

2.Num campo de futebol, o comprimento excede a largura em 50 cm. O perímetro de meio campo é 230 cm. As dimensões do campo de futebol são:

A. 60 x 110 B. 70 x 120 C. 80 x 130 D. 90 x 140

Resolução

C=l+50

Perímetro do meio campo é metade do perímetro,ou seja o perímetro total do campo é o dobro do perímetro do meio campo

P=2•Pm=2•230=460

Um campo de futebol tem um formato de um rectângulo então o perímetro é calculada com a forma do perímetro do rectângulo

P=2(c+l)

460=2(l+50+l)

460=2l+100+2l

4l=460-100

4l=360

l=90cm

C=l+50=90+50=140cm

As demissões do campo são 90cm x 140cm

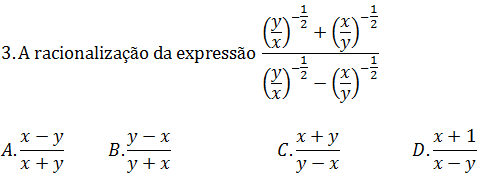
Resolução

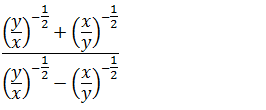
Vamos inverter as bases e os expoentes passagem a serem positivo

Vamos escrever a potência em raiz

Vamos multiplicar o numerador e denominador pelo par conjugado do denominador

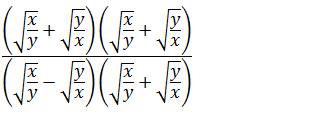
Sabemos que (a+b)(a+b)=a²+2ab+b² e (a+b)(a-b)= a²-b² aplicaremos esse conhecimento e ao quadrado iremos simplificar com a raiz quadrada.

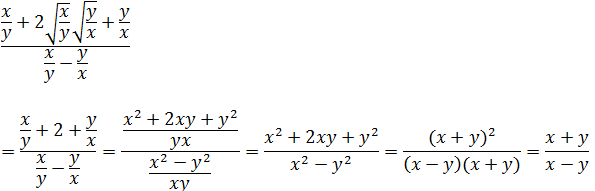
5.As soluções da equação

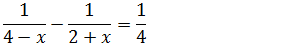
A)-8 e 2 B)-8 e -2 C) -8 ou -2 D) -8 ou 2

Primeiro vamos calcular o domínio

4-x≠0 e 2+x≠0

X≠4 x≠-2

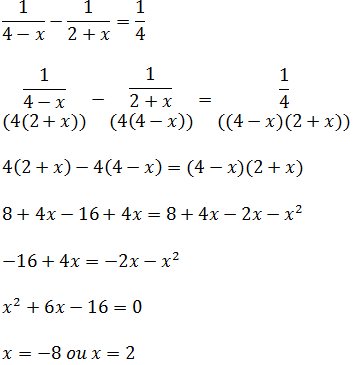
x=-8 ou x=2

Resposta x=-8 ou x=2

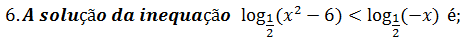
A. x<-3 B. x<-3 ᴧ x>2 C. x<-3 v x>2 D. { }

Domínio

x²-6>0 e -x>0

Ou seja;

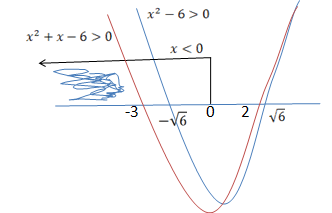
x²-6>0 e x<0

Agora vamos resolver a inequação Como a base e’ menor que um vamos inverter o sinal enveis de <, passara a ser >.

x²-6>-x

x²+x-6>0

x²+x-6=0

x=-3 ou x=2

x<-3 ou x>2

7.O domínio de existência de f(x) = lxl + 2 é:

A. x+2 se x≤0 -x+2 se x>0	B. x+2 se x≥0 -x+2 se x<0
C. x+2 se x≤-2 -x+2 se x>2	C. x+2 se x≥-2 x+2 se x<2

R; f(x) é x+2 se x+2≥0 ou seja se x≥-2, e x+2 se x-2<0 ou seja se se x<2.

8. Qual é a simplificação da preposição (a → ~b)v~C:

A.~(aᴧb)v~c B.~(aᴧb)vc C.-avbᴧ~c D. avb~c

(a →~b v~C

(~av~b)v~C

~(aᴧb)v~C

R;A simplificação da preposição (a → ~b)v~C é ~(aᴧb)v~C

9.A negação da preposição ∀x ∈ Z; x+1≤x é

A. ∃x ∉ Z; x+1>x B. ∃x ∉ Z; x+1>x C. ∃x ∈ Z; x+1>x D. ∃x ∈ Z; x+1≥x

R; A negação de ∀x ∈ Z; x+1≤x é ∃x ∈ Z; x+1>x

10.Sendo p → q uma proposição falsa, quais são os valores lógicos das proposições: i) ~p ᴧ q e

ii)-p ↔ (~pv q):

A. As duas falsas B. As duas verdadeiras C. i) Falsa e ii) Verdadeira D. i) Verdadeira e ii) Falsa

Como a preposição p→q é uma preposição falta então o valor lógico de p é f e o valor lógico de q é v

i) ~p ᴧ q= ~F ᴧ V=V ᴧ V=V

ii)~p ↔ (~pv q)=~F ↔ (~FvV)=V↔(VvV)= V↔V=V

R; As duas preposições são verdadeiras

11.O quociente da divisão do polinómio P(x) = x³+x² + x+ 1 por x +1 é:

A.x²-1 B.x²+1 C.x²+x-1 D.x²+x-1

Vamos colocar essa divisão sobre forma de fracção depois factorizar o polinómio x³+x² + x+ 1 e por fim simplificar.

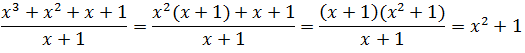
R; O quociente da divisão do polinómio P(x) = x³+x² + x+ 1 por x +1 é x² +1

13.A ordenada na origem da recta que passa pelos pontos A(1, 2) e B(2, -1) é:

A. -1 B. -3 C. 1 D.3

Resolução

primeiro vamos achar a equação da recta que passa por esse pontos depois disso vamos substituir x por zero para ter a ordenada na origem;

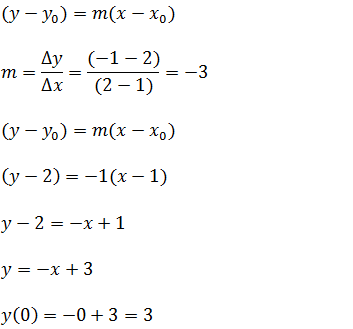
A ordenada na origem é 3

14.O coeficiente angular da recta tangente a curva f (x) = x³ + 2x no ponto x=1 é:

A. -5 B. -1 C.1 D.5

Resolução

O coeficiente angular da recta tangente a curva f (x) representa a derivada da curva no ponto dado (x=1) então primeiro vamos achar a derivada de f(x) e depôs vamos fazer x=1 e Assim temos a coeficiente angular;

f (x) = x³ + 2x

f’ (x) = 3x² + 2

m= f’ (1)= 3•1² + 2=3+2=5

15. Qual é a medida do ângulo a no triângulo?

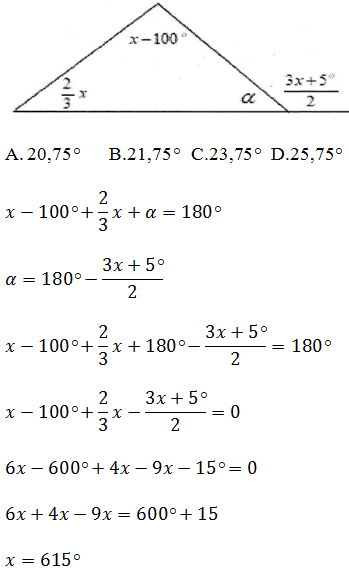
Não é possível. Em um triângulo os ângulos internos são sempre menores de 180°

16.Um paralelogramo cujos ângulos agudos medem 45° tem como comprimento dos lados 40 cm (base) e 18 cm. Qual é a área do paralelogramo?

A. 5 cm² B. 5,8cm² C.6 cm² D.6,08 cm²

A=b•h

h=l•sen(45°)

A=b• l•sen(45°)

A=40• 18•0,7

A=40• 18•√2/2

A=20•18•√2 cm²

A=360√2cm²≈509,04cm²

17.Numa prova de natação participar 7 nadadores, que disputam as medalhas de ouro, prata e bronze. De quantas formas diferentes se podem repartir estes 3 prémios? ( Não se admite Repetição)

A. 35 C.45 C.20A D.210

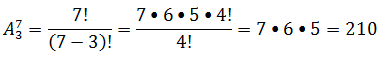
18.De 10 operários vão ser escolhidos 5 para irem trabalhar para uma obra. Quantos grupos diferentes se podem formar:

A. 252 B. 262 C. 30420 D.30240

Temos 10 operários queremos escolher 5 então para determinar o numero de grupos que se pode formar vamos usar combinação de 10 tomado 5

Podemos formar 252 grupos diferentes

Clique aqui para ver porque usamos combinação

19. O período da função g(x) = -2cos(3x – π) +1

20.O contradomínio da função g(x) = -2cos(3x – π) +1

A) -1≤ y ≤ 3 B) -3≤ y ≤ -1 C) -3≤ y ≤ 1 D) 1≤ y ≤ 3

Resolução

Cosseno de qual quer ângulo sempre varia de -1 a 1 o que quer dizer que -1≤cos(3x – π) ≤1 então o valor dessa expressão na função g(x) iremos substituir por -1 e 1 assim temos remos o contradomínio que seja ymin≤y≤ymax

Y1= -2(-1) +2+1=3

Y2 = -2•1 =-2+1=-1

O valor mínimo de y v -1 (ymini=-1 ) eo valor máximo de é 3 ( ymax=3)

ymin≤y≤ymax

R; o contradomínio é ymin≤y≤ymax subis-1≤y≤3