O que são Assimptotas ?
Assimptotas são rectas que o gráfico de uma determinada função tende a tocar e não toca.
Tipos de Assimptotas
Assimptota Oblíqua
A assimptotas Oblíqua (AO) é uma recta oblíqua que o gráfico tende a tocar mais não toca vejamos a assimptota oblíqua no gráfico abaixo;
Como calcular / encontrar assimptota Obliqua?
Assimptota Obliqua é uma recta linear “y=ax+b” para encontrar essa recta basta apenas calcular os valores de a e b, que são calculados a partes das formulas;
Encontrados esses valores de a e b temos assim a equação da assimptota Obliqua bastando substituir esses valores na formula da recta da assimptota Obliqua y=ax+b.
Assintota horizontal
A assimptotas horizontal (AH) é uma recta horizontal que o gráfico tende a tocar mais não toca vejamos a assimptota horizontal no gráfico abaixo;
Como calcular / encontrar assimptota horizontal?
Assimptota horizontal (AH) é calculado a partir do limite da nossa função quando x se aproxima de infinito.
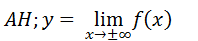
Assimptota Vertical
A assimptotas Vertical (AV) é uma recta vertical que o gráfico tende a tocar mais não toca vejamos a assimptota vertical no gráfico abaixo;
Como calcular / encontrar assimptota Vertical?
A assimptota Vertical (AV) é entrado a partir de uma análise, o limite da nossa função quando x se aproxima da assim vertical é infinito é essa base que usaremos basta encontrar o valor da Assimptota Verticais.
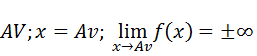
A Assintota Verticais é sempre um valor que não pertence ao domínio.
Resolução de exercícios de calculo de assinptotas
1.Encontre as assimptotas verticais, horizontal, obliquas para a função;
Resolução
Para Encontras as assimptotas verticais, horizontal, obliquas vamos usar as forma e o conhecimento teórico que aprendemos na explicação das assimptotas.
Assimptotas verticais
O valor provável da Assimptotas vertical é o valor que anula no denominador (que faz o denominador ser igual a zero)
Av; (x-1)²=0
x=1
Agora verificar se x=1 é uma Assimptota vertical calcando o limite da função quando x tende a 1.
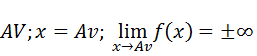
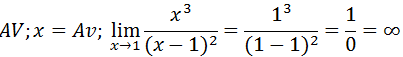
Como o limite de f(x) quando x tende a 1 da infinito então x=1 é Assimptota vertical
AV; x=1
Assimptotas Horizontal
Assimptota Horizontal Não existe gráfico.
Assimptotas Obliqua
Já vimos que a assimptotas Obliqua é uma recta do tipo “y=ax+b” a partir das formulas que vimos quando estudamos sobre assimptotas Obliqua vamos calcular o valor de a e b
Primeiro vamos calcular o valor de ‘a”
Agora vamos calcular o valor de “b”
Com os cálculos que fizemos constatamos que para a função
2.Encontre a assimptota vertical para a função;
O valor provável da Assimptotas vertical é o valo que anula no denominador (que faz o denominador ser igual a zero)
x-2=0
x=2
Agora verificar se x=2 é uma Assimptota vertical calculando o limite da função quando x tende a 2.
Como o limite de f(x) quando x tende a 2 não resultou em infinito então a recta x=2 não é Assimptota vertical(é apenas um ponto de descontinuidade e que não faz parte do domínio)
AV; Não existe nessa função
3.Encontre a assimptota vertical para a função;

O s valores prováveis da assimptotas verticais é o valor que anula no denominador (que faz o denominador ser igual a zero)
x²-9=0
x=±3
x=-3 ou x=3
Os valores prováveis da assimptotas verticais são x=3 e x=-3 devemos verificar se realmente são calculando limite da são quando “x” tende a esses valores se o limite for infinito é por que são.
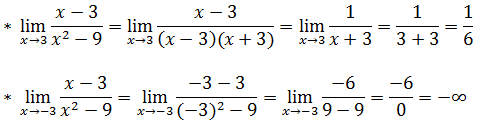
**Como o limite de f(x) quando x tende a 3 não resultou em infinito então a recta x=3 não é Assimptota vertical.
**Como o limite de f(x) quando x tende a -3 resultou em infinito então a recta x=-3 é Assimptota vertical.
AV; x=-3
4.Encontre as assimptotas verticais, horizontal, obliquas para a função;
Assimptota verticais
O valor provável da Assimptota vertical é o valo que anula no denominador (que faz o denominador ser igual a zero)
x+5=0
x=-5
Agora verificar se x=-5 é uma assimptota vertical calculando o limite da função quando x tende a -5.
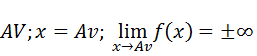
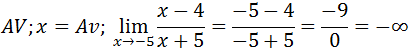
Como o limite de f(x) quando x tende a -5 da infinito então x=-5 é Assimptota vertical
AV; x=-5
Assimptota Horizontal
AH; y=1
Assimptota Oblíqua
Como nesse gráfico demos Assimptota Horizontal então assimptota Obliqua.
AO; Não existe.
5. Indique as assimptotas, Vertical, Horizontal e Obliqua para o gráfico abaixo;
* A assimptotas Vertical é uma recta vertical que o gráfico tende a tocar mais não toca para o gráfico acima a recta é x=1
AV; x=1
* A assimptotas Horizontal é uma recta horizontal que o gráfico tende a tocar mais não toca para o gráfico acima a recta é y=-2
AH; y=-2
* A assimptotas Obliqua é uma recta Obliqua que o gráfico tende a tocar mais não toca, e no gráfico acima não existe nenhuma recta oblíqua que o gráfico tende a tocar e não toca logo não existe assimptota Obliqua.
Ao; Não existe, nesse gráfico
Exercícios para praticar calculo de assintotas
1.Encontre as assimptotas verticais, horizontal e obliquas para a função;
2.Encontre a assimptotas vertical horizontal e oblíquas, para a função;
3.Encontre a assimptotas vertical para a função;
4.Encontre as assimptotas verticais, horizontal e obliquas para a função;
5. Indique as assimptotas, Vertical, Horizontal e Obliqua para o gráfico abaixo;
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …
Exercícios sobre limites e continuidades
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que:Como os limites …
Limites indeterminações do tipo zero sobre zero
Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a var…
Resolução de exercícios sobre limites trigonométricos
Uma vez que já vimos o limite trigonométrico fundamental a gora e a hora de usar esse conhecimentos …




