Classificação de uma sucessão

Sucessão limitada

Uma sucessão diz-se limitada se todos termos da sucessão estão compreendidos em determinado intervalo a e b finito ou seja na sucessão temos um majorante (o maior termo) e um minorante (o menor termo).

Exemplo;

a_n = (4,2,0,-2)

Note: que a sucessão “tem um inicio e um fim”

Começa no 4 e termina no -2

O majorante é o maior termo da sucessão, logo o majorante é na sucessão é 4

O minorante é o menor termo da sucessão, portanto o minorante é na sucessão é -2

Mais exemplos de sucessões limitadas

b_n = (-3,-6,-9,-12,-15)

v_n = (25,30,35,45,50)

k_n = (25,30,35,…,50)

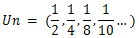
Observação  U_n é limitada pois tem todos os termo da sucessão estão compreendidos no intervalo de ½≤U_n<0

Sucessão ilimitada

Uma sucessão diz-se ilimitada se os termos da sucessão são infinitos. Uma sucessão ilimitada só tem majorante ou minorante e nunca majorante e minorante.

a_n = (1,2,3,4,5…)

“Note; que a sucessão tem um inicio mais não tem fim”

Começa no 1 e não termina

1 é o minorante na sucessão

Mais exemplos de sucessões ilimitadas

b_n = (3,6,9,12,15…)

v_n = (23,20,17,14,11…)

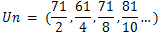
Classificação de uma sucessão quanto a monotonia

Sucessão crescente

Uma sucessão diz-se crescente quando na medida que a ordem aumenta os termos também vão crescendo.

U_(n+1)> U_n

U_(n+1)– U_n>0

Exemplos

s_n = (13,16,19,21,35…)

Sucessão decrescente

Uma sucessão é decrescente quando na medida que a ordem aumenta os termos vão decrescendo.

U_(n+1)< U_n

U_(n+1)– U_n>0

Exemplos

f_n = (40,36,33,21,15…)

x_n = (-1,-7,-11,-21 …)

Sucessão não crescente

Uma sucessão diz-se não crescente quando na medida que a ordem aumenta os termos não crescem

U_(n+1)≤ U_n

U_(n+1)– U_n≤0

Exemplos

o_n = (12,12,7,5,5,3…)

y_n = (11,7,4,2…)

Nota; toda sucessão decrescente é não crescente mais nem toda sucessão não crescente é decrescente

Sucessão não decrescente

Uma sucessão diz-se não decrescente quando na medida que a ordem aumenta os termos não decrescem

U_(n+1)≥ U_n

U_(n+1)– U_n≥0

Exemplo

l_n = (5,7,9,9,11…)

e_n = (1,6,11,16…)

Nota; toda sucessão crescente é não decrescente mais nem toda sucessão não decrescente é crescente

Sucessão constante

Uma sucessão diz-se constante quando os termos da sucessão são constante

U₁= U₂=U₃=U₄=U_n

Exemplo

q_n = (6,6,6,6,6…)

Classificação de uma secessão quanto a convergência

Sucessão convergente

Uma sucessão é convergente se converge para um valor k ou seja o seu limite é um valor numérico

Exemplo

Sucessão divergente

Uma sucessão é divergente se ela não for convergente converge ou seja o não tem limite.

Exemplo

d_n = (2,9,17,25,33…)

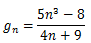
Sucessão infinitamente grande positiva

Uma sucessão diz-se infinitamente grande positiva se o limite for igual a mais infinito

Exemplo

m_n = (34,63,94,124,155…)

j_n=3n-9

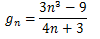
Sucessão infinitamente grande negativa

Uma sucessão diz-se infinitamente grande negativa se o limite for igual a menos infinito

Exemplo

h_n = (-3,-10,-17,-24,-33…)

j_n=-35n-4

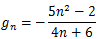
Sucessão infinitamente pequena (infinitésimo)

Uma sucessão diz-se infinitamente pequena ou infinitésimo se o limite for igual a zero

Exemplo

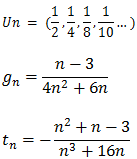
Exercício de aplicação

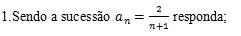
a) Classifique a sucessão quanto a monotonia

b) Classifique a sucessão quanto ao limite

c)Quanto a convergência

Resolução

a)Para classificar a sucessão quanto a monotonia

a_(n+1)-a_n

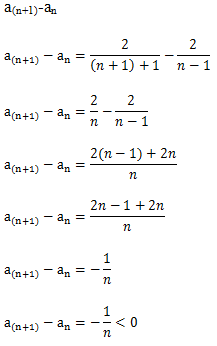
R: Quanto a monotonia a sucessão a_n é decresceste

b) Para classificar a sucessão quanto ao limite devermos primeiro procurar saber se a sucessão tem majorante e minorante.

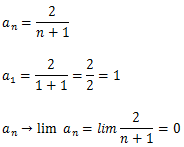
R: A sucessão quanto ao limite ela é limitada pois tem um majorante e um minorante o majorante é 1 e o minorante é 0

c) Quanto a convergência a sucessão é convergente (converge para 0)

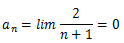
a) Classifique a sucessão

b)Quais são os majorantes e minorantes

Resolução

Primeiro vamos classificar b_n quanto a monotonia

Para tal usaremos a formula b_(n+1)-b_n e vamos analisar o sinal dessa diferença

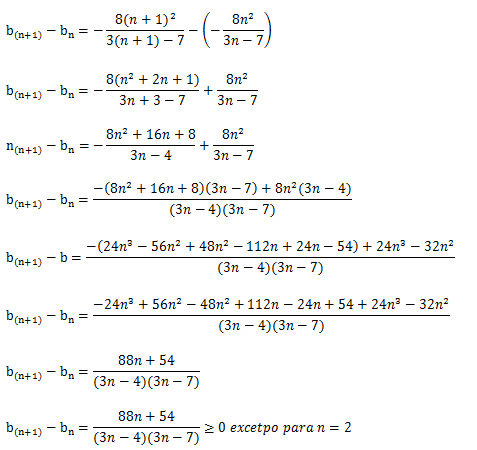
O numerador da expressão b_(n+1)-b_n  é sempre positivo(para valores de n natural) e o denominador oscila

R: Então a sucessão b_n Quanto a monotonia é oscilante.

*Quanto ao limite a sucessão é ilimitada pois o limite é infinito

*Quanto a convergência a sucessão é divergente pois não tem limite (não converge para nenhum valor)

b)Para achar o majorante e minorante Samos calcular o primeiro e ultimo termo

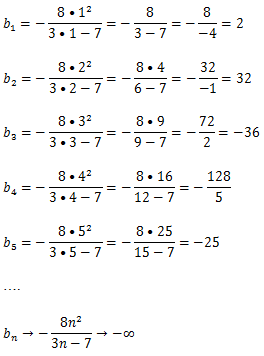
O majorante é o maior termo nessa sucessão o majorante é 32 e como a sucessão é limitada e tem majorante então a sucessão não tem minorante.

3.para a sucessão a_n=cos(n) responda;

a) Na e uma sucessão limitada ou ilimitada?

b) Indique os 3 primeiros termos dessa sucessão a_n

Resolução

a)A sucessão na é limitada pois os valores de cós(n) então contido no intervalo fechado ( -1≤a_n≤1 )

b) Os 3 primeiros termos dessa sucessão nasão;

a₁=cos1 ,a₂=cos2 e a₃=cos3

Recomendamos ver:

Conceito de sucessão e termo geral de uma sucessão qualquer

Progressão aritmética (PA)

Progressão geométrica (PG)

---