Limites de funções de variável real

Representação de limite

Seja da uma função f(x) e desejamos saber qual é o limite da função quando nos se aproximamos de um determinado valor “a” então podemos escrever ;

a – é a tendência ( valor em que se aproximamos)

f(x) é a função que pretendemos saber o limite quando se aproximamos de “a“

Valor de um limite

Então L é o valor do limite.

Cálculo de limites

Numa primeira fase para o cálculo de limite usaremos tabela para facilitar a compressão.

Calcule os seguintes limites;

Iremos construir uma tabela onde iremos se a aproximar de três (pois a variável x no nosso exercício tende a 3) e iremos a analisar os valores da função f(x)=x²

x	f (x)= x²
2,7999	7,8394
2.9998	8,9988
2,9999	8,9994
3	—
3,0001	9,0006
3,0002	9,0012
3,0003	9,0018

Quando se aproximamos de 3 a nossa função fica muito próximo de 9 então diremos que o limite da função quando se aproximamos de 3 é nove e iremos escrever;

Iremos construir uma tabela onde iremos se a aproximar de dois (por a variável x no nosso exercício tende a 2) e iremos a analisar os valores da função f(x)=x+4

x	f (x)= x+4
1,8899	5,8899
1,9098	5,9098
1,9999	-5,9999
2	—
2,0001	6,00001
2,0002	6,00002
2,0003	6,00003

 
Quando se aproximamos de dois a nossa função fica muito próximo de seis então diremos que o limite da função quando se aproximamos de dois é seis e iremos escrever;

Iremos construir uma tabela onde iremos se a aproximar de dois (por a variável x no nosso exercício tende a 2) e iremos a analisar os valores da função f(x)=x⁴-1

x	f (x)= x⁴-1
0,8899	-0,2080
0,9898	-0,0202
0,9999	-0,00001
1	—
1.0001	0,00001
1,0002	0,00004
1,0003	0,00006

 Quando se aproximamos de um a nossa função fica muito próximo de zero então diremos que o limite da função quando se aproximamos de zero é zero e iremos escrever;

Limite de cálculo imediato

Seja dado uma função f(x) contínua em “a” pertencente “a” o domínio o limite da nossa função ponto a será igual a ao valor da função no ponto “a”

Calcule sabendo que as funções abaixo são continuas calcule os limites na abcissa indicados

A nossa função é f(x)=x⁴-3 e a abcissa é dois como a nossa função  é continua o valor do limite no ponto dois será igual ao valor da função no ponto dois.

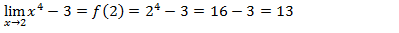
A nossa função é f(x)=5x-7 e a abcissa é zero como a nossa função  é continua o valor do limite no ponto zero será igual ao valor da função nesse  ponto.

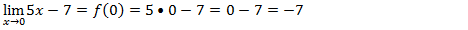
A nossa função é f(x)=senx e a abcissa é quatro como a nossa função  é continua o valor do limite no ponto quatro conforme já dissemos será igual ao valor da função nesse  ponto.

Exercícios de limite calculo I

Exercícios sobre limites para praticar

1. Recorrendo a uma tabela calcule os limites asseguir;

2. Calcule os seguintes limites;

---

Veja mais uma das nossa aulas