Derivada de uma função

Depois de termos aprendendo o conceito de derivada agora é a hora de aprendemos a calcular derivada de funções.

Primeiramente aprenderemos como calcular deriva de uma função to tipo f(x)=xⁿ, deriva quando a variável x esta dentro da raiz e a também a deriva de uma constante onde ir os ver que a deriva de uma constante é igual a zero.

Derivada da função f(x)=xⁿ

Para fazer a demonstração da derivada da função f(x)=xⁿ iremos usar o conceito de derivada usando limites .Demonstração

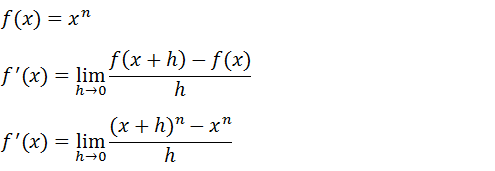
Vamos recorrer ao binómio de Newton para fazer o desenvolvimento do caso notável (x+h)ⁿ que fazendo o desenvolvimento e substituindo no limite a derivada para acha temos:

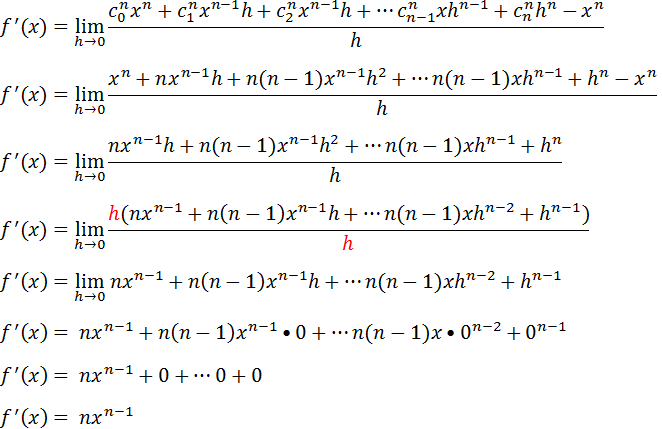
“Se nos tivermos uma função f(x)=xⁿ para achar a sua derivada a gente abaixo o n e no exponente no n a gente tira um “

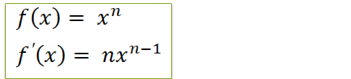
Determine a derivadas as funções abaixo

a)Calcule a derivada da função y=x³

y=x³

y’= 3x³-¹

y’= 3x²

b) Calcule a derivada da função y=2x⁶

Para calcular essa derivada devemos saber que quando uma constante esta a multiplicar uma função a deriva será igual a derivada da função que a contaste esta multiplicar vezes a própria constante.

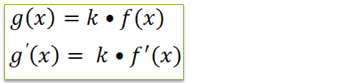
y=2x⁶

y’=2•(x⁶)’

y’= 2•6 x⁶-¹

c)Calcule a derivada da função y=x-⁴

y=x-⁴

y’=-4 x-⁴-¹

y’=-4 x-⁵

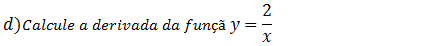
Com o conhecimento de derivada de função que nos já aprendemos a até aqui aparentemente não podemos resolver essa deriva mais é possível sim, vamos passar o x para o numerador  uma vês que eles esta elevado a um quando passa para o numerador o exponente fica menos um, que quando x passa para o numerador podemos facilmente derivar.

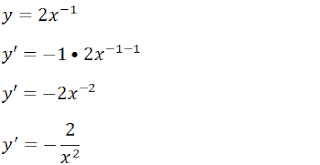
Para derivar essa função vamos transformar a raiz em uma potencia uma vez que ainda não aprendemos derivadas de funções irracionais.

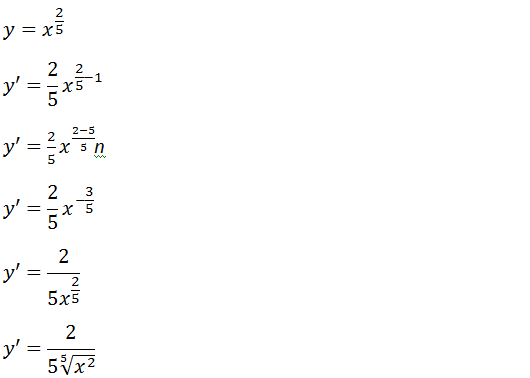
Derivada uma constante

y=a

y=ax°

y’= a•0 x°-¹

y’=0

“A derivada de uma constante é igual a zero“

Calcule a derivadas das funções constantes

a) Calcule a derivada da função y=3

Três é uma constante então a derivada da função y=3 será zero

a)y=3

y’=0

b) Calcule a derivada da função y=√5

y=√5 tem derivada nula (igual a zero pois √5 é uma constante)

b)y=√5

y’=0

c) Calcule a derivada da função y= π

A derivada da função y= π será zero pois π é uma constante (π=3,14…)

c) Calcule a derivada da função y= π

y= π

y’=0

Mais exercícios derivada de uma constante

a)y=5 y’=0	c)y=4 π y’=0	e)y=0 y’=0
b)y=-2000 y’=0	d)y=√2 y’=0	f)y=-34 y’=0

Derivada de uma função linear

y=ax

y=ax¹

y’= a•1 x¹-¹

y’=ax°

y’=a

“A derivada de uma função lineary=ax+b é y’=a uma vez que b é uma constante e a derivada de uma constante é zero e a devida de y=ax é a.”

y=ax+b

y’= (ax)’+(b)

y’= a+0

y’= a

Exercícios resolvidos deriva de uma função linear

a)Calcule a derivada da função y=3x

y=3x

y’=3

b) Calcule a derivada da função y=5x

y=5x

y’=5

c) Calcule a derivada da função y=6x

y=6x

y’=6

Derivada de uma soma

Tendo uma função composta por uma soma de duas ou mais funções e nos queremos a achar a sua derivada basta fazemos a soma da derivada de cada uma das funções.

y=u+v

y’=u’+v’

Exercícios resolvidos  sobre derivada de uma soma

a) Calcule a deriva da função f(x)= x⁴+x⁶

A função f(x)= x⁴+x⁶ representa a soma da função g(x)= x⁴ e a função k(x)= x⁶ então estamos diante de uma derivada de uma soma e como vimos acima a derivada de f(x) será igual a soma da derivada das duas funções.

f(x)=x⁴+x⁶

f’(x) = (x⁴)’+(x⁶)’

f’(x)= 4x³+6x⁵

b)Calcule a deriva da função f(x)=3x²-x⁵+9

f(x)=3x²-x⁵+9

f’(x)= (3x²)’-(x⁵)’+(9)’

f’(x)=3•2x-5x⁴+0

f’(x)=6x-5x⁴

c)Calcule a deriva da função g(x)=5x²⁵-4x⁵-4x+12

g(x)=5x²⁵-4x⁵-4x+12

g’(x)=(5x²⁵)’-(4x⁵)’-(4x)’+(12)’

g’(x)=5•25x²⁴-4•5x⁴-4

g’(x)=125x²⁴-20x⁴-4

d)Calcule a derivada da função g(x)=-x⁵-4x²

g(x)=-x⁵-4x²

g’(x)=-5x⁴-8x

e)Calcule a derivada da função f(x)=-5x⁴-8x

f(x)=-5x⁴-8x

f(x)=-20x⁴-8

Exercícios para praticar derivadas de funções

---

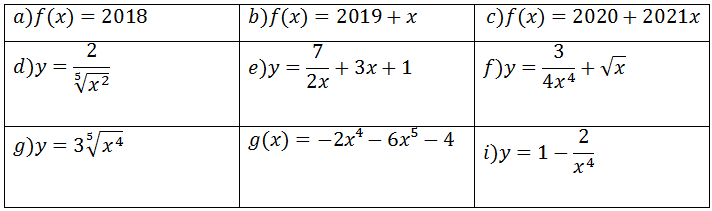
Quintal aprender outras derivadas