Estudo da primeira derivada
Seja uma função f(x) continua
Assim temos representado os gráficos de uma função f (x) e sua derivada f ’(x)
Notamos claramente que;
| ]- ∞, b[ | b | ]b, d[ | d | ]d,+ ∞[ | |
| f (x) | ↗ | Máximo | ↘ | Mínimo | ↗ |
| f ’(x) | + | 0 | – | 0 | – |
Ou seja
* Sempre que a deriva da função f(x) for positiva a função f(x) é crescente.
f ’(x)>0 f (x) é crescente
* Sempre que a deriva da função f(x) for negativa a função f(x) é decrescente.
f ’(x)<0 f (x) é decrescente
Ponto máximo e ponto mínimo são pontos em que a primeira derivada é nula (f ’(x)=0 )
Como saber se um ponto é máximo ou mínimo
* Um ponto é máximo se a derivada muda de positivo para negativo.
* Um ponto é mínimo se a derivada muda de negativo para positivo.
Exemplo de aplicação
a)Determine os extremos máximos e mínimos para a função;

Resolução
Para encontrar os pontos máximos e mínimos devemos achar a primeira derivada e depois igual a zero

Vamos igualar a derivada a zero
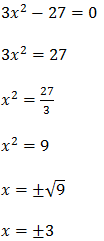
x=-3 e x=3
Para saber qual deles é máximo e qual é mínimo vamos esboçar o gráfico da primeira deriva
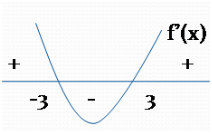
Como no ponto x=-3 a derivada muda de positivo para negativo diremos que
X=-3 extremo máximo
Como no ponto x=3 a derivada muda de negativo para positivo diremos que
X=3 extremo mínimo
Não deixe de ver;
Como fazer calculo aproximado usando derivadas ?
Estudo da segunda derivada
| f (x) | U | Ponto de infecção | ∩ |
| f ’’(x) | – | 0 | – |
Ou seja
* Sempre que a segunda deriva da função f(x) for positiva a função f(x) tem concavidade voltada para cima.
f ’’(x)>0 f (x) tem concavidade voltada para cima.
* Sempre que a segunda deriva da função f(x) for negativa a função f(x) tem concavidade voltada para baixo.
f ’’(x)<0 f (x) é tem concavidade voltada para baixo.
Ponto de infecção é o ponto em que a função muda de sentido de concavidade e a segunda derivada nesse ponto é nula (f ’’(x)=0 )
Exemplo de aplicação
b)Determine o ponto de infecção para a função
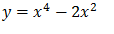
Resolução
Para calcular o ponto de infecção precisamos de achar a segunda derivada e depois igual a zero
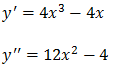
Como ponto de infecção é um ponto em que a segunda derivada é igual a zero, iremos igual a segunda derivada a zero
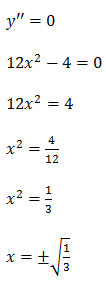

Teste da segunda derivada
Também é possível saber se um ponto é máximo ou mínimo a partir do teste da segunda derivada vamos representar uma função f(x)

Notamos que o extremo máximo é b e nesse ponto a função f(x) tem concavidade voltada para baixo isso significa que a segunda deriva é negativa. e d é um extremo mínimo e nesse ponto a função tem concavidade voltada para cima isso significa que a segunda deriva é positiva
De um modo geral podemos dizer que;
Extremo máximo se; f ’’(x )=0 e f ’’(x)<0
Extremo mínimo se; f ’’(x )=0 e f ’’(x)>0
Exemplo de aplicação
C) Calcule os extremos máximos e mínimos e encontre os respectivos pontos máximos e mínimo para a função;
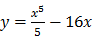
Resolução
Para encontrar os pontos máximos e mínimos devemos achar a primeira derivada e depois igual a zero
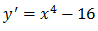
Vamos igual a primeira derivada a zero
y’= 0

Para ver qual e máximo e qual e mínimo vamos usar o teste da segunda deriva
Como no ponto x=-2 a primeira derivada é igual a zero e a segunda derivada é negativa diremos que x=-2 é um extremo máximo
Como no ponto x=2 a primeira derivada é igual a zero e a segunda derivada é positiva diremos que x=-2 é um extremo mínimo.
Agora vamos calcular os pontos máximos e mínimos da função
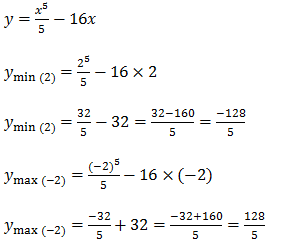
Acréscimo de uma função
Conceito de acréscimo(∆y) de uma função f(x) Seja dada a função f(x) cujo o gráfico ê a baixo repres…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Aplicação da primeira e segunda derivada extremos e ponto de infecção
Estudo da primeira derivada Seja uma função f(x) continua Assim temos representado os gráficos de um…
Calculo aproximado usando derivada
Definição derivada Para percebemos como usar as derivadas para fazer o cálculo aproximado vamos usar…
Progressão geométrica (PG)
Progressão geométrica é um tipo de sucessão em que a razão entre os termos consecutivos é constante.…
Progressão aritmética (PA)
O que é progressão aritmética ? Progressão aritmética é um tipo de sucessão em que a diferença entre…
Classificação de uma sucessão
Sucessão limitada Uma sucessão diz-se limitada se todos termos da sucessão estão compreendidos em de…
Sucessões (O que é um sucessão numérica)
Sucessão é uma sequência de números que obedece uma determinada lei de formação a qual chamamos de t…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …
Exercícios sobre limites e continuidades
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que:Como os limites …
Limites indeterminações do tipo zero sobre zero
Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a var…
Resolução de exercícios sobre limites trigonométricos
Uma vez que já vimos o limite trigonométrico fundamental a gora e a hora de usar esse conhecimentos …
Limites laterais (Limite lateral à esquerda e limite lateral à direita)
Seja dado uma função f(x) cujo o gráfico é representado na figura acima Como achar os limites latera…
Continuidade de função e Tipos de descontinuidades
Continuidade de função Seja dado uma função f(x) e um ponto qualquer x=a que pertence ao domíni…
Derivada de uma função exponencial
Para acharmos a derivada de uma função exponencial vamos o usar a definição de deriva…
Derivada de uma função usando definição
Definição de derivadas Chamamos de derivada da função f(x) no ponto qualquer a inclinação …
Derivada de uma função
Depois de termos aprendendo o conceito de derivada agora é a hora de aprendemos a cal…
Limites trigonométricos
Para resolver exercícios de limites trigonométricos devemos antes conhecer e ter o domínio…
Limite notável (limite exponencial)
O Limite notável é base para a resolução de diversos limites exponencial épraticamente impossível re…
Limite exponencial (limite de Euler)
Limite exponencial são conhecido vulgarmente como limite de Euler, a indeterminação nos li…
Limites indeterminações do tipo infinito sobre infinito
Limites contendo indeterminações do tipo infinito sobre infinito são limites&nbs…
Limites indeterminações do tipo infinito menos infinito
Agora que já aprendemos as propriedades dos limites , como resolver exercícios de lim…
Limites de funções de variável real
Representação de limite Seja da uma função f(x) e nós desejamos saber qual é o limite da f…
Propriedades usadas no cálculo de limites
As propriedades usadas do cálculo de limites na maioria das vezes são empregues de forma …
Derivada de funções implícitas
Antes de aprendermos a derivar uma função implícita é necessário saber o que é uma fu…
Derivada de funções paramétricas
Derivada de funções paramétricas Seja y=f(t) e x=g(t) nesse caso podemos afirmar que…
Cálculo de limite usando L’Hospital (Cálculo de limite usando derivadas)
Regra L’Hospital para o calculo de limite A regra de L’Hospital consiste em utilizar o conhecimento …



















