Operações entre conjuntos
As principais operações entre conjuntos são;
* União (U)
* Intercessão (∩)
* Complementar de um conjunto
* Diferença (A/B)
* Diferença simétrica ∆
União de conjuntos (AUB)
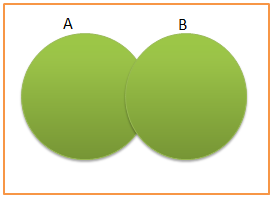
A união consiste basicamente em unir os dois conjuntos isto é agrupar todos elementos do conjunto eu estão a ser unidos e transformar em um só conjunto com todos elementos dos conjunto que estão a ser unidos.
1.Para os conjuntos A={1,3,5,7} e B={2,4,6,8,10}
Determine a união entre esses dois conjuntos (AUB)
Confirme já dissemos a união de dois conjuntos A e B será um conjunto que surge com a “junção” de todos os elementos do conjunto A e B (sem repetir os elementos)
AUB={1,2,3,4,5,6,7,8,9,10}
2.Seja dado o conjunto A={4,5,7} e B={2,4,8}
A união entre esses dois conjuntos (AUB) é;
AUB={2,4,5,4,5,7,8,9}
Nota: Não repetimos o nenhum elemento, (o 4 esta nos dois conjuntos não precisamos de repetir ele duas vezes).
3.Sendo o conjunto A={a,e,i,o,u} e B={a,b,c,e,f,d,f}
Ache o conjunto que surge da união entre esses dois conjuntos (AUB)
AUB={a,b,c,e,f,d,f,o,u}
Intercessão de conjuntos (A∩B)
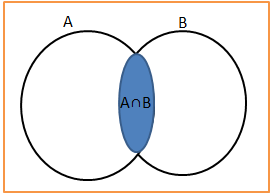
Fazer a intercessão de dois ou mais conjuntos consistem em levamos os elementos que estão simultaneamente nos dois conjuntos e fazer um novo conjunto.
1. A={a,e,i,o,u} e B={a,b,c,e,f,d,f,g,h}
Determine a intercessão entre esses dois conjuntos (A∩B)
A intercessão entre os conjuntos A e B será todos os elementos do conjunto A que estão no conjunto B, ou seja são os elementos que pertencem simultaneamente ao dois conjuntos. Esse caso os elementos que estão simultaneamente no conjunto A e no conjunto B são “a , e” então a intercessão entre esses dois conjuntos é;
A∩B={a,e}
Complementar de um conjunto
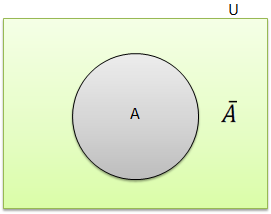
Se tivermos um conjunto A e queremos o seu complementar, Basta no conjunto Universo tivemos os elementos que estão no A o conjunto que se forma será o complementar de A.
1.Seja dado o conjunto A={a,i} e U={a,e,i,o,u}
Encontre o conjunto complementar de A
O conjunto complementar de A é o conjunto de todos elementos que estão no nosso universo e não estão no conjunto A, nesse caso em concreto os elementos que estão no Universo e e não estão no A são “e,o,u” então o complementar de A será o conjunto formado por estes elementos
Â={e,o,u}
Diferença entre dois conjuntos(A/B)
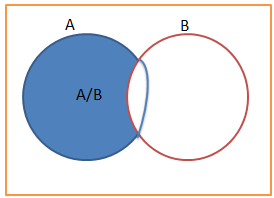
A diferente de B (A/B) são os elementos do conjunto A que não estão no conjunto B.
1.Seja dado o conjunto A={1,3,4,5,7} e B={2,4,8,9}
Encotre os conjuntos;
a)A/B
b)B/A
A/B={1,3,5,7}
B/A={2,8,9}
Diferença simétrica A∆B
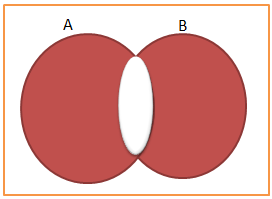
A diferença simétrica entre os conjuntos representa a união entre os conjuntos tirando a intercessão. A Diferença simétrica entre o conjunto A e B será;
* A∆B= (AUB)/(A∩B)
1.Seja dado o conjunto A={a,e,i,o,u} , B={a,b,c,e,f,d,f,g,h} e C={d,e,f,g,h,i,j,k}
Determine ;
a)A∆B
b)C∆B
Resolução
a) A∆B é a união ente os conjuntos A e B tirando a intercessão nesse caso a união é AUB={a,b,c,e,f,d,f,g,hi,o,u} e a intercessão é A∩B={a,e} a união tirando a intercessão temos A∆B logo;
A∆B={b,c,d,f,g,h}
B) seguindo o mesmo procedimento de fazer a intercessão de CUB e depois tirar os elementos da intercessão entre B∩C temo que;
C∆B={a,b,c,i,j,k}
Exercícios para praticar teoria de conjuntos
1.Seja dados os conjuntos A,B e C onde A={1,3,4,5,6,7}, B={1,3,6,9} e C={0,2,4,6,8}
Determine os seguintes conjuntos
A)AUC
B)A∩C
C)BUC
D)(AUB)/C
E)A/B
f)A∆C