Continuidade de função
Seja dado uma função f(x) e um ponto qualquer x=a que pertence ao domínio de f(x) dissemos que a função f(x) é continua no ponto x=a se ;
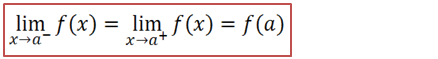
Ou seja uma função é continua no ponto x=a se os limites laterais forem iguais e forem igual ao valor da função nesse ponto.
Observações sobre continuidade de funções; `
* Para que a função seja continua não basta só os limites laterais serem iguais é necessário também que sejam igual ao valor da função nesse ponto.
* Uma função só pode ser continua no ponto pertencente o domínio da função.
Tipos de descontinuidades
1.Descontinuidade eliminável (ou removível)
Uma função diz se descontinua eliminável no ponto x=a se os limites laterais forem iguais porem diferentes do valor da função nesse ponto.
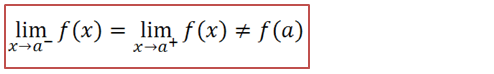
Nota; Os limites laterais devem ser iguais e iguais a um valor numérico, não pode ser infinito.
2.Descontinuidade primeira espécie
Uma função diz se descontinua primeira espécie no ponto x=a se os limites laterais forem diferentes.
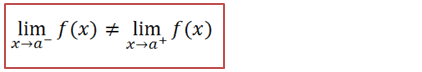
Nota; Os limites laterais devem ser diferentes e cada limite lateral deve ser igual a um valor numérico, não pode ser infinito.
3.Descontinuidade segunda espécie
Uma função diz se descontinua segunda espécie no ponto x=a se um dos limites laterais for infinito.
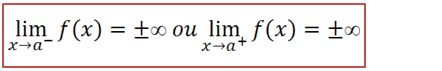
Nota; Basta um dos limites laterais ser infinito a função é descontínua segunda espécie.
Resolução de exercícios continuidade de função
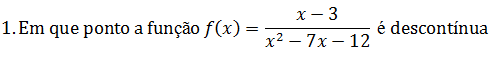
Uma função é contínua em pontos pertencentes ao domínio então é descontínua em todos pontos que não pertencem ao domínio então para descobrir os pontos de descontinuidade iremos achar os pontos que não pertencem ao domínio pois estes são os pontos de descontinuidade. Como temos fuma fracção para achar o domínio basta recordar que não existe divisão por zero ou seja vamos dizer que o denominador deve ser diferente de zero. “x²-7x-12≠0” e resolvermos essa equação quadrática teremos os pontos de descontinuidade
x²-7x-12≠0
(x-3)(x-4)≠0
x-3 ≠0 e x-4≠0
x ≠3 e x≠4
A nossa função é descontinua no ponto x=3 e x=4 pois estes são os pontos que não pertencem ao domínio de f(x).
2. Determine o valor de a de modo que a função seja continua ponto x=3
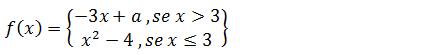
Uma função é contínua se os limites laterais forem iguais e estes por sua vez serem iguais ao valor da função nesse ponto e o nosso ponto é x=3;
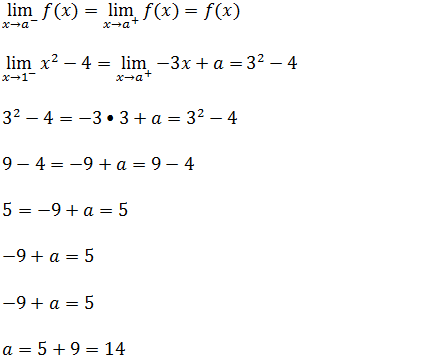
3. Verifique se a função é continua no ponto x=4
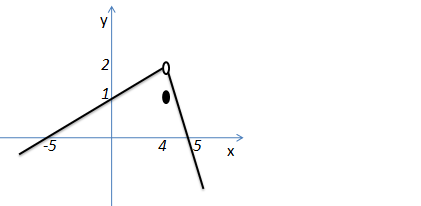
Para saber se a função é contínua ou não no ponto x=4 vamos achar os limites laterais e o valor da função nesse ponto.
Se aproximando de quatro pela esquerda temos dois

Se aproximando de quatro pela direita temos dois

No ponto x=4 o valor de y é 1 então

No ponto x=4 a função não é continua pois f(4) é diferente do valor dos limites laterais.
Resolução de exercícios classificação de descontinuidade
1.Verifique se a função f(x) é continua no ponto x=1 se não forem continua indique o tipo de descontinuidade

Resolução
Para saber se a função é contínua no ponto vamos calcular os limites laterais nesse ponto.
Conforme já explicamos o limite lateral a esquerda a gente leva onde o intervalo é menor ou igual (onde apontou para esquerda)
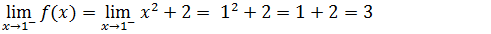
Limite lateral a direita s gente leva a parte de maior (onde apontou para direita)
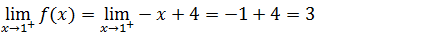
Para saber o valor de f(1) vamos na segunda expressão (pois ela contem a parte de igual a um ) substituir onde vem x por um
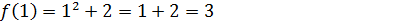
Como os limites laterais são iguais no ponto x=1 e igual a valor da função no ponto x=1 então a função é contínua no ponto x=1.
2.Verifique se a função f(x) é continua no ponto x=2 se não forem continua indique o tipo de descontinuidade
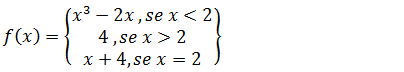
Seguiremos o mesmo procedimento que do exercício anterior para saber se a função é continua ou não.
Limite lateral a esquerda levamos a parte que apontou para esquerda (a parte de menor)
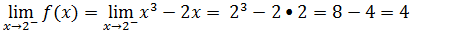
Limite lateral a direita levamos a parte que apontou para direita (a parte de maior)

Para calcular f(2) vamos pegar a função e onde vem x=2, que é a terceira condição no nosso exercício f(x)=x+4 e substituir x por 2
f(2)=2+4=6
Como os limites laterais são iguais ( no ponto x=2) e deferente do valor da função no ponto x=2 então diremos que a função é descontínua eliminável no ponto x=2.
3.Determine os limites laterais para a função f(x)no ponto x=4

Primeiro calcularemos o limite lateral a esquerda.
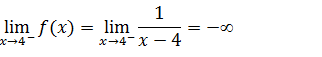
Como um dos limites laterais é infinito não precisamos calcular o outro limite lateral podemos logo afirmar que a função é descontínua segunda espécie.
4.Verifique se a função g(x) é continua no ponto x=0 se não forem continua indique o tipo de descontinuidade
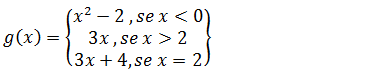
Tal como fizemos nos exercícios anterior para saber se a função é contínua ou descontinua vamos achar os limites laterais.
Limite lateral a esquerda levamos a parte que apontou para esquerda (a parte de menor)
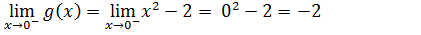
Limite lateral a direita levamos a parte que apontou para direita (a parte de maior)
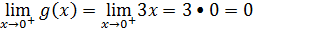
Como os limites laterais são diferentes não precisamos de calcular o valor da função no ponto para saber que esta é descontínua primeira espécie.
Exercícios sobre continuidade de função para praticar
1.Para os gráficos asseguir indique qual delas é contínua, e os que não forem contínua classifique o tipo de descontinuidade.
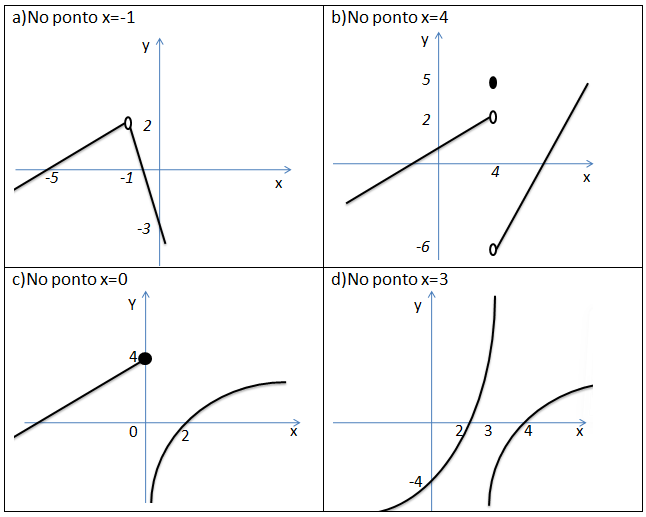
2.Continuidade e classificação de descontinuidades exercícios

Veja mais uma das nossa aulas
Resolução de exercícios sobre limites trigonométricos
Uma vez que já vimos o limite trigonométrico fundamental a gora e a hora de usar esse conh…
Limites trigonométricos
Para resolver exercícios de limites trigonométricos devemos antes conhecer e ter o domínio…
Limite notável (limite exponencial)
O Limite notável é base para a resolução de diversos limites exponencial é praticamente impossível r…
Limite exponencial (limite de Euler)
Limite exponencial são conhecido vulgarmente como limite de Euler, a indeterminação nos li…
Limites indeterminações do tipo zero sobre zero
Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a var…
Limites indeterminações do tipo infinito sobre infinito
Limites contendo indeterminações do tipo infinito sobre infinito são limites&nbs…






