Integral de funções com fracções

Integral de funções que resultam em arctag(x)

Essa é uma integral imediata, bastando apenas nos recordar da derivada da função arctangente (a função arctan(x)) , Quando aprendemos derivada vimos que a derivada da função arctan(x) é a função 1/(x²+1), O que pelo conceito de integral quer dizer que a integral da função  1/(x²+1) é a função arctan(x) e podemos escrever usando o símbolo de integral como sendo;

Sempre tivermos uma integral definida no fim depois de achar a solução devemos adicionar uma contaste arbitraria para generalizar a nossa solução vamos adicionar a contaste a nossa solução

Usando as formulas aprendidas anteriormente

Formula generalizada da integral que resultam em arctangente

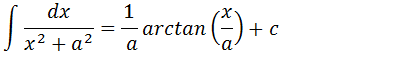
Demonstração da formula

Iremos transformar a nossa fracção em uma função onde no numerador temos u²+1 para podemos aplicar que a integral se transforme em uma integral ja conhecida para isso vamos evidenciar o “a” no denominador

Recorrendo ao método de substituição, onde substituiremos x/ a por u

x/a=u

x=au

dx=adu

Vamos simplificar o “a²” do numerador com um “a” do denominar e depois tirar o “a” que sobra no denominar para fora da integral

Sabemos que a integral de 1 sobre u²+1 tem como resultado arctan(u)

Vamos substituir u por x/a e assim temos demonstração

Exercícios de calculo de integrais que resultam em funções trigonométricas inversas arcseno

Colocando o 4 em forma de potencia de expoente 2

Usando a forma que aprendemos acima temos como solução

Vamos colocar cinco na raiz e elevar ao quadrado

Podemos colocar 9 como 3²

Seja ; x-2=u

dx=du

Como dissemos que u=x-2 onde tem u iremos substituir por x-2

Podemos escrever 16 como sendo 4²

Fazendo; 3x+4=u

3dx=du

dx=du/3

Substituindo na nossa integral temos;

Tirando o 3 para fora da integrar

Essa integral tem como resultado a função arctagente

Podemos multiplicar 3 e 4 e assim temos o resultado final da nossa integral

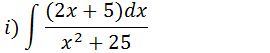
Vamos separa a nossa integral em duas integrais

A primeira integra é uma integral do tipo du/u que resulta em ln|u| onde o nosso u é x²+25 e a segunda integral tem como em arctagente, mais na segunda primeiramente vamos tirar o 5 para fora da integral transformar 25 em 5 ao quadrado;

Fazendo a simplificação temos

Integrais com fracções de uma diferença de quadrados no denominador

Integrais com fracções do tipo

Essa integral tem como resultado;

Demonstração da integral com fracções

Quando aprendemos casos notáveis vimos que x²-a²=(x-a)(x+a)

Vamos trabalhar com a fracção que esta dentro da integral separar ela em duas fracções

Vamos calcular o valor de “p” e “q”

1=p(x+a)+q(x-a)

1=px+pa+qx-qa

1=(p+q)x+pa-qa

p+q=0 e pa-qa=1

p=- q

-qa-qa=1

-2qa=1

q=-1/2a

p=-q=1/2a

Vamos colocar o “1/2a” em envidecia

Vamos substituir essa espressao na nossa integral

Vamos tira o “1/2a” para fora da integral e separa a nossa integral em duas integrais

Sabemos que integral de 1/u é igual a ln|u| onde para a primeira integral o nosso u é “x-a” e para a segunda integral o u e’ “x+a”

Aplicando a propriedades de diferença de logaritmos temos;

Exercícios para praticar integrais com fracções

Vamos colocar o denominador na formula x²-a² , onde para isso vamos transformar 9 em 3²

Usando a formula que aprendemos acima temos

Vamos substituir 16 por 4²

Usaremos o método de substituição

Seja ; 5x+4=u

5dx=du

dx=du/5

Vamos tira o 5 para fora da integral e depois aplicar a nossa formula de integrais com fracções

Como u=5x+4 vamos substituir u por essa expressão

Aulas relacionadas

• Calculo integral
• Derivada de arctan
• Derivada de funções logaritmos
• Integral de funções exponencial
• Derivada de funções trigonométricas
• Limites trigonométricos