Movimento circular
Movimento circular é basicamente um movimento curvilíneo com raio constante, São exemplos de movimento circular o ponteiro de um relógio, a roda de um caro, as pás do ventilador, Helicóptero etc.
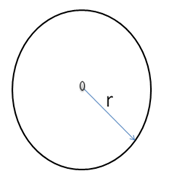
Grandezas angulares
| Grandezas angulares | Relação com grandezas não angulares (lineares) |
| Velocidade angular ( ω) | |
| Fase (ϕ) |
Observação; se tiver uma velocidade linear v para termos a velocidade angular (ω) basta dividir por r ou seja a para termos grandezas angulares vamos dividir as não angulares (lineares) pelo raio (r).
Movimento circular uniforme
Movimento circular uniforme é aquele em que o modulo da velocidade permanece constante.
Equações do movimento circular
Durante o Movimento circular temos uma variação de fase ∆ϕ durante um pequeno intervalo de tempo ∆t (Fase é um ângulo ϕ descrito durante o movimento).
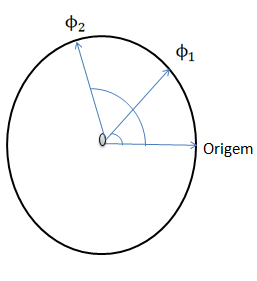
A velocidade de a angular ω pode ser obtida a partir da reacção entre grandezas angulares e não angulares.
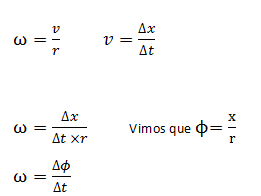
Período e frequência
Imaginemos uma situação um corpo de girando em torno de um eixo com uma velocidade ω constante. Chamamos de período o tempo que o corpo leva para realizar uma volta completa
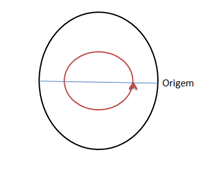
Quando o corpo realiza uma volta tempo (t) e igual ao período (T) t=T ele perle percorre 360 grãos para realizar uma volta completa ϕ=2 π
.
Substituindo ϕ=2 π ; t=T temos ;
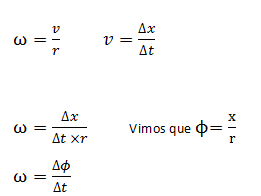
O que também pode ser escrito na formula;
Também podemos expressar o período como sendo a razão entre o tempo t e o número de voltas (n) que ele realiza neste tempo t
Convêm expressarmos uma grandeza física que nos dirá o numero de voltas eu o corpo realiza a cada t segundos a qual chamaremos que frequência (f).
A partir do conceito e da expressão matemática nota-se claramente que a frequência e o inverso do período.
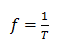
f=2πω
Exercício para consolidar a matéria
1) Um disco de raia 0.25m realiza 40voltas em 8segundos determine;
1.Um disco de raia 0.25m realiza 40voltas em 8segundos determine;
a)O período
b)A frequência
c)A velocidade angular
d)A velocidade linear
Resolução
Dados
n=40voltas
t=8s
R=0.25m
a)O período pode ser determinado pela expressão
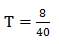
T =0.2 s
b)Dissemos que a frequência é o inverso do período
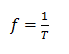
f=1/0.2
f=5Hz
c) A velocidade angular pode ser obtida usando a expressão;
ω=2πf
ω=2×3.14×5
ω=6.28×5
ω=31.4rar/s
d) Para determinar a velocidade linear uma vez que já temos a velocidade angular vamos usar a relação
v=ωr
v=ωr
v=31.4×0.25
v=7.85m/s
2.Um corpo em movimento circular uniforme realiza 60rps qual o seu período.
Resolução
Um corpo realiza 60rps isso significa que o corpo realiza 60 voltas em 1 segundo ou seja n=60voltas e t=1s dai podemos determinar o período
Equação da fase ϕ em função do tempo t (ϕ(t))
Podemos obter a equação da fase de dois métodos
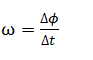
Com variação de fase igual a fase menos fase inicial ( ∆ϕ=ϕ -ϕₒ) e ∆t=t-tₒ como estudamos o movimento a partir do instante t=0s a variação do tempo será igual a t (∆t=t)
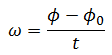
ϕ -ϕₒ=ωt ϕ = ϕₒ+ωt
Aceleração centrípeta
No movimento circular sempre temos uma aceleração dirigida ao centre que chamamos de aceleração angular (também pode ser chamada de aceleração normal) essa aceleração e devido a variação do sentido e da direcção da velocidade.
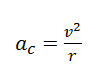
Como v=ωr temos;
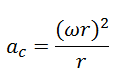
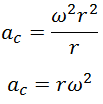
Exercícios de aplicação
1.um móvel em movimento circular uniforme faz 120rpm determine:
a) A frequência
b)A velocidade angular
c) A aceleração centrípeta sabendo que o raio fale 0.6m
d) A equação da fase em função do tempo sabendo que parte da origem
e) Fase no instante t=100s
f) As equações lineares
Resolução
a)Faz 120rpm significa que faz 120 rotações (voltas) em 1minuto ;
n=120 e t=1minuto=60s
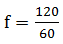
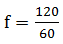
f=2Hz
b)Sabemos que ω=2πf
ω=2πf
ω=2×3.14×2
ω=6.28×2
ω=12.56rad/s
c)Tendo a velocidade angular e o raio e fácil determinar a aceleração centrípeta
d)Vimos que ϕ = ϕₒ+ωt calculamos a velocidade angular o resultado obtido foi ω=12.56rad/s e como parte da origem ϕₒ=0
ϕ = 0+12.56t
ϕ = 12.56t
e)Vamos na equação da fase substituir por t=100s
ϕ = 12.56×100
ϕ = 1256rad
f)Para termos as equações angulares vamos multiplicar as equações angulares pelo raio na alinha “c” fomos dito que r=0.6m
v=ωr=12.56×0.6=7.54m/s
x= ϕr= 12.56t×0.6=7.54t
Acoplamento de polias
O acoplamento de polias é muito usado nas máquinas mecânicas e não podemos encontrar o acoplamento de polias a bicicletas
Acoplamento de por correia
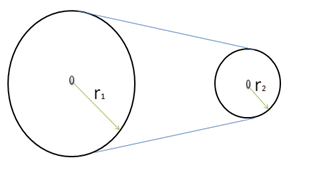
Nesse caso as duas polias move-se com mesma velocidade linear v1=v2
Acoplamento por mesmo eixo de rotação
Uma víeis que as polias giram entorno do mesmo eixo eles terão a mesma velocidade angular. (ω1=ω2)
Aplicação
1.Duas polias são acoplados em torno do mesmo eixo sendo r1=2m v1=50m/s determine o raio da segunda polia sabendo que ele gira a uma velocidade de 80m/s (v2=80m) Resolução Como eles são acoplados em torno do mesmo eixo de rotação ω1=ω2 ω1=ω2
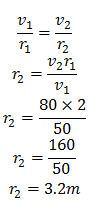
Movimento circular uniformemente variado
Neste tipo de movimento o modulo da velocidade e variável fazendo com que exista uma aceleração angular
Resumo
| Grandezas | Expressão |
| Aceleração angular | α é constante |
| Velocidade angular | ω = ωₒ+αt |
| Fase | |
| Equação de Torricelli | ω² = ωₒ²+2α∆ϕ |