Força centrípeta
Quando um corpo realiza um movimento circular uniforme ela esta sujeita a uma aceleração centrípeta (ac) que e responsável pela mudança da direcção do movimento.
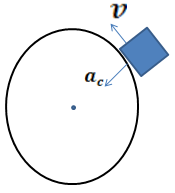
A aceleração centrípeta sempre se dirige para o centro. Sendo o corpo de massa m sujeita a uma celebração centrípeta (ac) surge uma força que chamaremos de força centrípeta e representaremos por fc.
Usando a segunda lei de Newton podemos concluir e expressar matematicamente a força centrípeta como sendo;
fc=m•ac
Quando abordamos o Movimento uniforme circular vimos que a aceleração centrípeta pode ser expressa em função da velocidade, a partir da expressão;
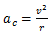
Substituindo essa expressão na equação da força centrípeta temos;
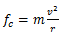
Exercícios de aplicação sobre Força centrípeta
1.Um carro de massa 2000kg percorre uma estrada com forma a figura indica, com uma velocidade constante de 4m/s determine a forma normal que a estrada exerce sobre o carro;
Resolução
Vamos representar as forças que actua no caro que são nomeadamente o peso e a força normal .
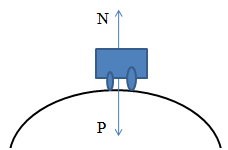
Como o corpo descreve uma trajectória circular a resultante será a forca centrípeta
P-N=fc
2. Um camião pretende fazer uma curva horizontal de raio 20m com uma velocidade de 6m/s determine o coeficiente de atrito entre os pneus do camião e a estrada de modo a fazer essa curva sem despistar
Resolução
Vamos representar as forcas que actua no carro;
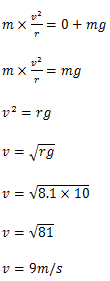
No eixo Y como não a movimento
N-P=0
N=P=mg
Para o eixo horizontal vamos usar segunda lei de Newton e como horizontal só temos a forca de atrito ela será igual a forca resultante centrípeta.
fa=fc
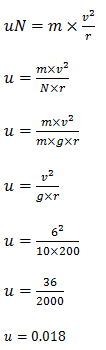
3. Detro de um globo de morte um moto motociclista realiza um movimento circular de raio 8.1m determine o valor da velocidade mínima no ponto mais alto do globo.
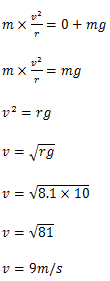
Resolução
Vamos representar as forcas que actua no corpo.
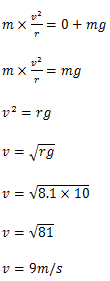
A forca resultante é a forca centrípeta e podermos expressar de acordo com a 2ª lei de Newton como sendo;
fc=N+P
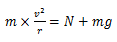
A velocidade é mínima quando N=0
Força elástica
A forca elástica esta sempre quando presente tentamos comprimir uma mola não só, como também em eleáticos e cordas de borrachas.
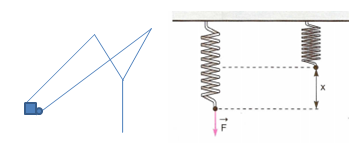
x– deformação elástica da mola.
As molas são diferente para cada tipo de material exemplo, note que ao comprimir uma mola de caro exercemos mais forca em relação a quando comprimimos uma mola de cama.
Porque e mais fácil comprimir a mola de cama do que de carro?
Isso deve-se ao grão de faculdade que as molas de caro oferecem em relação as molas da cama.
O grão de dificuldade que as molas oferecem chamaremos de constante elástica e representaremos por (k)
Lei de Hooke
A forca elástica (fe) é directamente proporcional a deformação (x) e depende da constante elástica do material ( k).
fe=k•x
Aplicação
1.A cortante elástica de uma mola é de 40N/m e deformada 20cm determine o valor força elástica
Resolução
Vamos aplicar a lei de Hooke para resolver o problema.
Dados
K=40N/m
X=20cm=0.2m
fe=k•x
fe=40•0.2
fe=8N