Limites indeterminações do tipo infinito menos infinito

Agora que já aprendemos as propriedades dos limites , como resolver exercícios de limites agora veremos como calcular um limite que envolve/tenha uma indeterminação do tipo infinito menos infinito.

O que saber para saber resolver limites com indeterminações do tipo infinito menos infinito

Demonstração
Vamos considerar 1/x como sendo uma função f(x) e como a variável esta se aproximar de infinito vamos substituir x por valores grandes.

x
10000	0.0001
100000	0.00001
2000000	0.0000005
888888888	0.00000001
99999999999	0.0000000001
996776678888	0,000000000001
9999999998899	0,0000000000001
…	…
∞	0

Quando a variável x assume valores muito grandes (quando se aproxima de infinito) a função tende a zero então podemos concluir que o limite da função é zero.

Demonstração

Vamos considerar x como sendo uma função f(x) e como a variável esta se aproximar de infinito vamos substituir x por valores grandes.

x	f(x)=x
234577	234577
3444444	3444444
546789000	546789000
8800888884	8800888884
90099999999	90099999999
996776678888	996776678888
999000999999889	999000999999889
…	…
∞	∞

Quando a variável x assume valores muito grandes (quando se aproxima de infinito) a função f(x)=x também tende a infinito  então podemos concluir que o limite da função é infinito.

Demonstração

Vamos considerar √x como sendo uma função f(x) e como a variável esta se aproximar de infinito vamos substituir x por valores grandes.

x	f(x)= √x
20034577	4467
38944444	6240.54
46789000	6840.24
800800888884	894874.79
90099999999	300166.62
996999776678888	31545303.27
16000000000000000000	4000000000
…	…
∞	∞

Quando a variável x assume valores muito grandes (quando se aproxima de infinito) a função f(x)= √x  também tende a infinito  então podemos concluir que o limite da função é infinito.

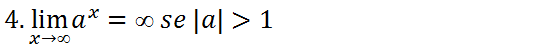
Demonstração

Vamos considerar a=2 (Nota podemos escolher qualquer valor de a desde que satisfaça a condição acima referido)

Vamos considerar 2^x como sendo uma função f(x) e como a variável esta se aproximar de infinito vamos substituir x por valores grandes.

x	f(x)= 2˟
30	1073741824
7389	204473937968879…
…	…
∞	∞

Quando a variável x assume valores muito grandes (quando se aproxima de infinito) a função f(x)= 2˟  também tende a infinito  então podemos concluir que o limite da função é infinito.

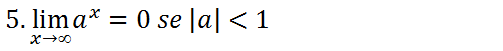
A demonstração desse limite também pode ser feita de forma análogo as demonstrações dos anteriores limites.

Cálculo de limites envolvendo indeterminações do tipo infinito menos ínfimo.

O calculo de limite com inseminações do tipo infinito menos infinito pode ser feito usando os seguintes passos;

Primeiro passo substituir o x pela tendência para certificar se realmente é uma indeterminação do tipo infinito menos infinito.

Segundo passo evidenciar o temo de maior grão e aplicar as propriedades acima referidos.

Exercício de cálculo de limites indeterminações do tipo infinito menos ínfimo.

Exercício 1

Resolução

Primeiro vamos substituir onde vem x pela tendência

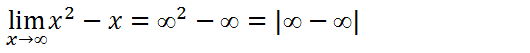
Para solver este limites vamos evidenciar o termo de maior grão para o exercício em quês tão o maior grão é o x²

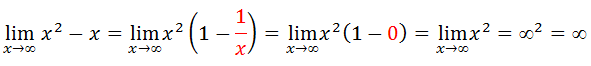
Exercício 2

Resolução

Primeiro vamos substituir onde vem x pela tendência

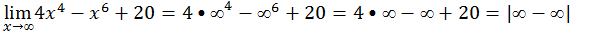
Para solver este limites vamos evidenciar o termo de maior grão para o exercício em quêstão o maior grão é o x⁶

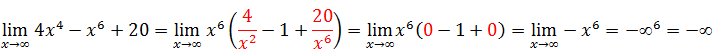
Exercício 3

Resolução

Primeiro vamos substituir onde vem x pela tendência

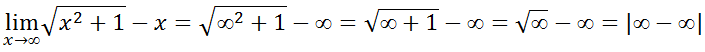
Para solver este limites vamos evidenciar o termo de maior grão para o exercício em questão o maior grão é o x²

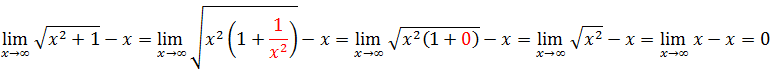
Outro método de resolução

Quando nós temos uma indeterminação do tipo infinito menos infinito com expressões dentro da raiz podemos recorrer ao par conjugado para resolver o exercício com essa indeterminação.

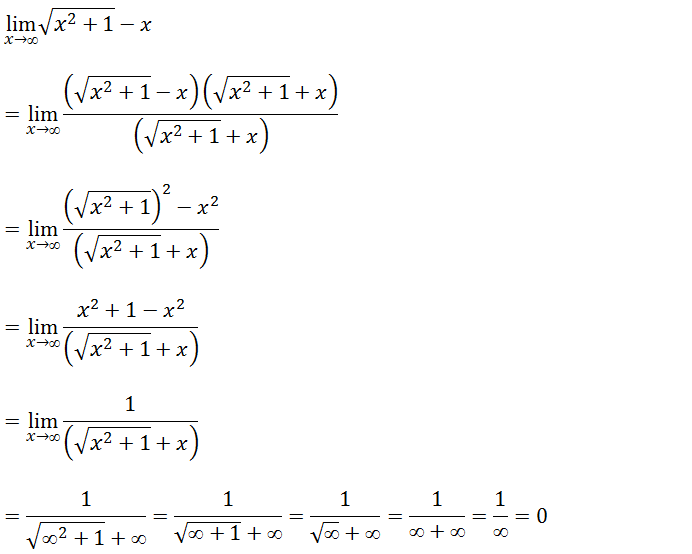
Exercício 4

Primeiro vamos substituir onde vem x pela tendência

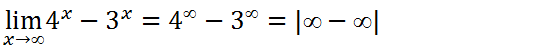
Para solver este limites vamos evidenciar o termo de maior grão para o exercício em quêstão o maior grão é o quatro elevado a x

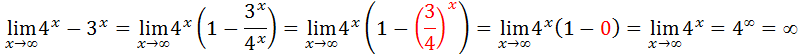
Exercícios de limites indeterminações infinito menos infinito para praticar

Usamos os conhecimentos adquiridos a partir dessa aula e das aulas anteriores de calcule os seguintes limites:

---

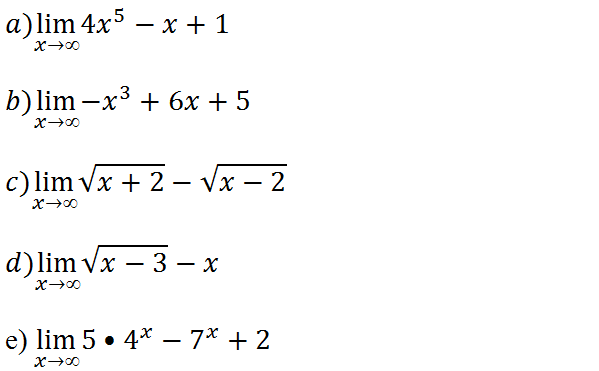
Veja mais uma das nossa aulas

---