Domínio de existência
Domínio de existência de uma função f(x) ou expressão representa o conjunto de favores “x” na qual a função esta definida, ou seja são os valores que a variável x pode assumir.
Domínio de existência de uma função algébrica inteira
a) f(x)=x+1
A variável x pode assumir qualquer valor então o domínio é IR
Df:x∈R
b) f(x)=-3x²+3x+1
A variável x pode assumir qualquer valor então o domínio é IR
Df:x∈R
c) f(x)=x⁴-15x+4
A variável x pode assumir qualquer valor então o domínio é IR
Df:x∈R
Domínio de funções irracionais
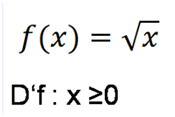
Nb; Não existe em IR raízes de números negativos (raiz de índice par) por isso a expressão que estiver dentro da raiz deve ser positiva (o que significa dizer que deve ser Maior ou igual a zero).
Agora se o índice for impar o domínio será IR pois existe raiz (de índice impar) para qualquer valor seja positivo ou negativo.
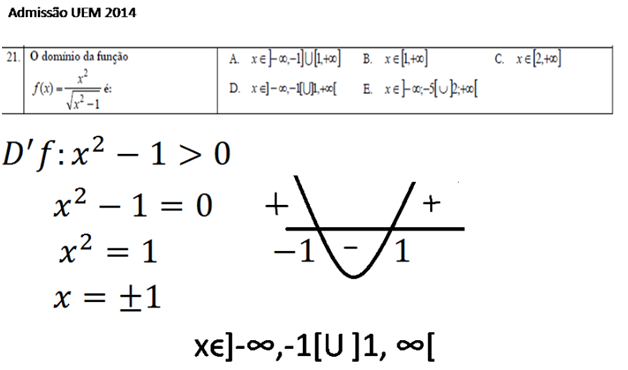
Domínio de funções fraccionais
Ex1.
Ex2.
Domínio de funções com raiz no denominador
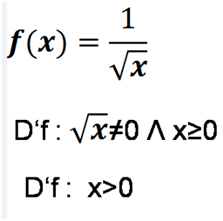
Nb; por estar no denominador dissemos que deve ser diferente de zero e por estar na raiz dissemos que deve ser maior ou igual a zero. Dizer diferente de zero e maior ou igual a zero equivale a dizer que deve ser maior que zero.
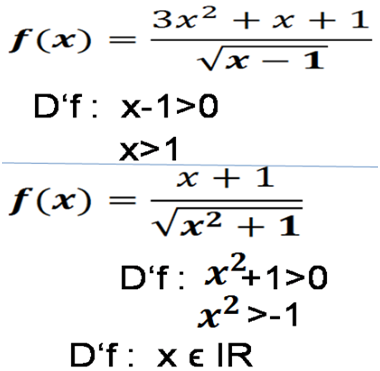
Domínio de existência de funções logoritmicas.
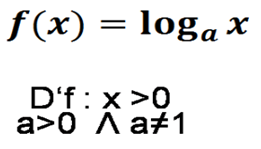
Nb; Não existe logoritmo com logaritmano ou base menor ou igual a zero, a base também deve ser diferente de um.
Exercícios dos exames de admissão sobre domínio de existência.
Assimptotas (Assimptota horizontal, Assimptota Vertical e Assimptota Oblíqua)
O que são Assimptotas ? Assimptotas são rectas que o gráfico de uma determinada função tende a tocar e não toca. Tipos de Assimptotas Assimptota Oblíqua A assimptotas Oblíqua (AO) é uma…
Limites de funções de variável real
Representação de limite Seja da uma função f(x) e nós desejamos saber qual é o limite da função quando nos se aproximamos de um determinado valor “a” então podemos escrever ; a – …
Trigonometria no triângulo rectângulo
Trigonometria no triângulo rectângulo e Identidade trigonométrica fundamental Para estudamos e compreendermos as relações trigonométricas no triângulo, vamos desenhar a um triângulo. O lado a chamarem…
Trigonometria tabela de ângulos especiais
Tabela de ângulos especiais em grãos Tabela de ângulos especiais em radiano Agora que já conhecemos a os valores de cos(x) , tan(x) , ctg(x) para os ângulos especiais vamos aprender ; 👉Trigonome…
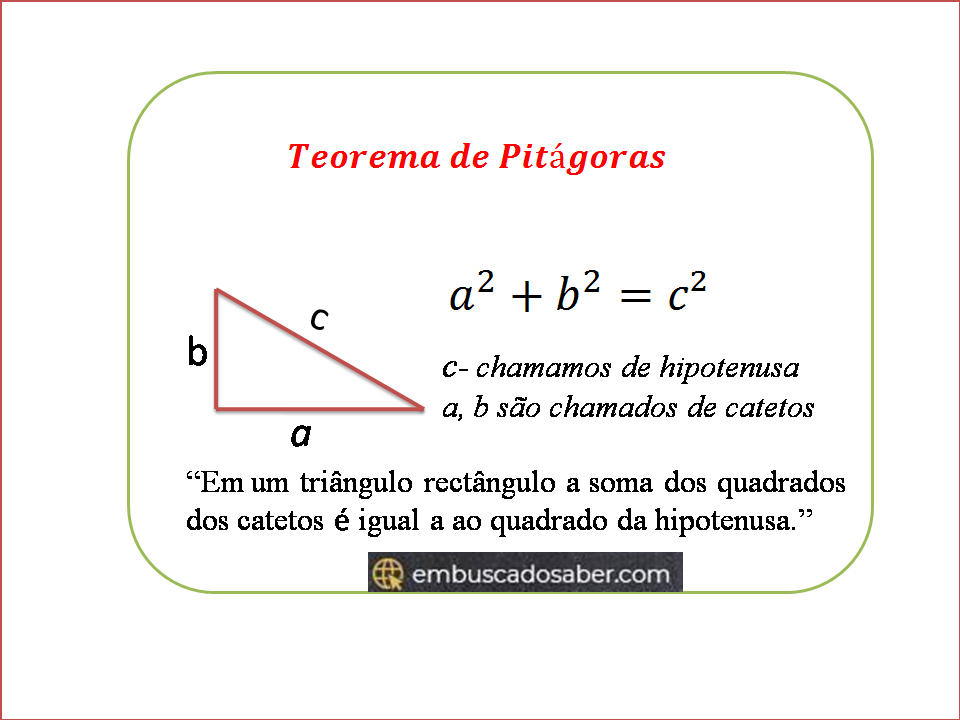
Teorema de Pitágoras (demonstração e resolução de exercícios)
O teorema de Pitágoras ajuda-nos a resolver diversos exercícios de geométrica. Enunciado do Pitágoras Para um triângulo rectângulo a soma dos quadrados dos catetos é igual a ao quadrado da h…
Pingback: Resolução de exame de matemática I 2021 admissão UEM - Embuscadosaber