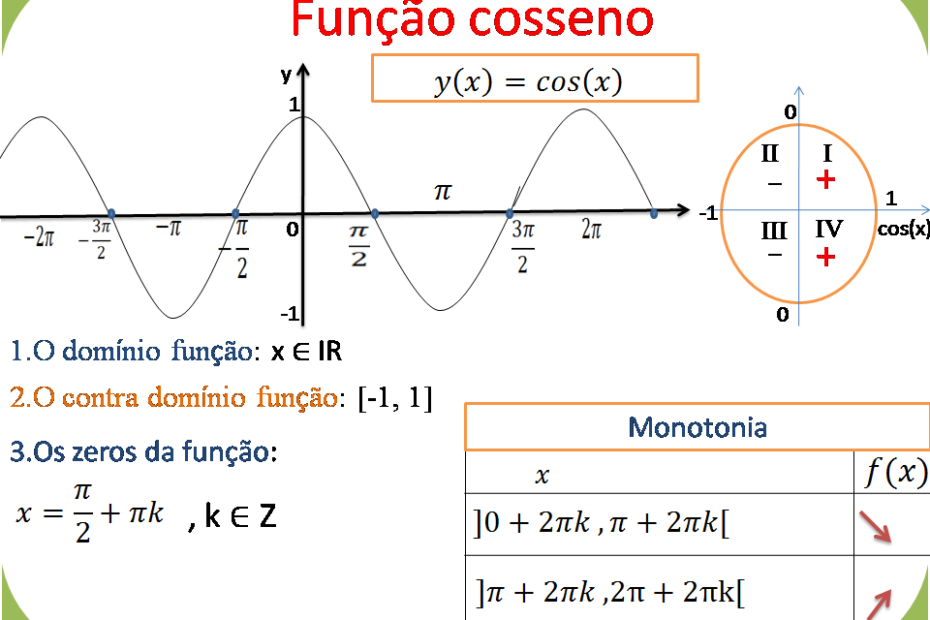
Função cosseno y=cos(x)
Representação gráfica da função y=cos(x)
Para representar o gráfico da função seno iremos construir uma tabela onde atribuiremos valores e x e encontrares com base nesses valores o valor de y.
| x | y=cos(x) |
| 0 | 1 |
| π/2 | 0 |
| π | -1 |
| 3π/2 | 0 |
| 2 π | 1 |
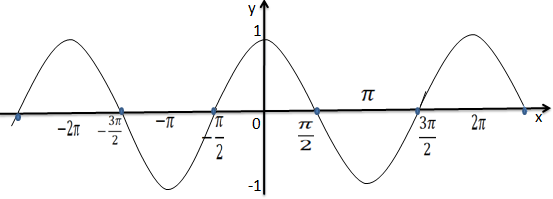
Dominio x ∈ R
Contra domínio y ∈ [-1,1]
Zeros x=π/2+2πk, sendo que k ∈ Z
Máximos: x=2πk,sendo que k ∈ Z
Mínimos: x= π+2πk,sendo que k ∈ Z
Paridade: Par
Monotonia
Variação do sinal
Representação gráfica da função f(x)=cos(x+b)
Esse tipo de função é feito a partir da função g(x)=cos(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=cos(x+b) a partir da função g(x)=cos(x) vamos;
– Deslocar b unidades para esquerda se b for positivo
– Deslocaremos b unidades para directa se b for negativo
Representação gráfica da função f(x)=cos(x)+c
Esse tipo de função é feito a partir da função g(x)= cos(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=cos(x)+c a partir da função g(x)= sen(x) iremos;
– Transladar a função f(x) b unidades para cima se b for positivo
– Transladaremos a função f(x) b unidades para baixo se b for negativo
Representação gráfica da função y=acos(x)
Esse tipo de função é feito a partir da função g(x)= cos(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=cos(x)+c a partir da função g(x)= sen(x) vamos;
– Multiplicar por a os valores de y= cos(x). Assim sendo a amplitude da função f(x)=acos(x) será [-a,a].
Exercícios resolvidos para fazer gráficos de funções trigonométricas
1.Represente graficamente a função y=cos(x)-3, e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
Primeiro vamos construir o gráfico da função g(x)=cos(x)
Vamos transladar duas unidades para cima e assim temos a função f(x)=cos(x)-3 a partir da função g(x)=cos(x)
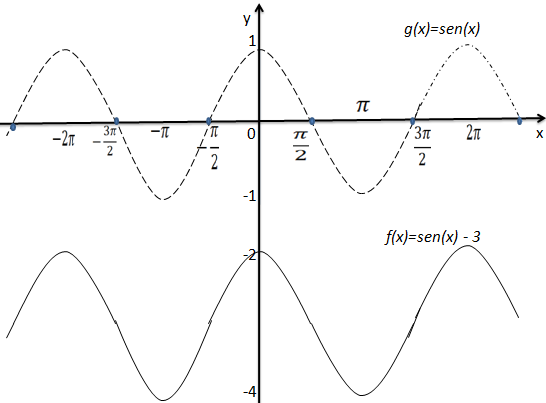
a) O domínio da função é R
b) O contradomínio é [-4,-2]
c) A ordenada na origem conforme podemos ver no gráfico é y=2.
d) A função intercepta não eixo das abcissas logo não tem zeros.
2.Represente graficamente a função y=cos(x+π), e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
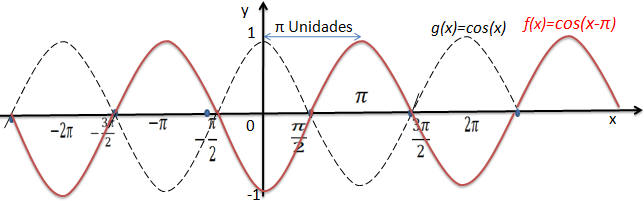
Primeiramente vamos construir o gráfico da função g(x)=cos(x)
Vamos transladar π unidades para esquerda e assim temos a função f(x)=cos(x+π ) a partir da função g(x)=cos(x)
3.Faça gráfico da função f(x)=2cos(x-π/4)-1
Para fazer o gráfico da função primeiro devemos fazer o gráfica da função h(x)=2cos(x-π/4) e depois deslocamos uma unidade para baixo.
E para fazer o gráfico da função h(x)=2cos(x-π/4) demos fazer o gráfico da função g(x)=cos(x-π/4) e multiplicamos por 2.
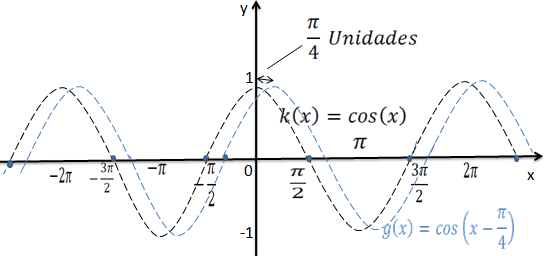
Sendo que para fazer o gráfico da função g(x)=cos(x-π/4) primeiro devemos fazer o gráfico da função k(x)=cos(x) e transladar π/4 unidades para direita.
Vamos transladar π/4 unidades para direita e assim temos a função g(x)=cos(x+π/4 ) a partir da função k(x)=cos(x)
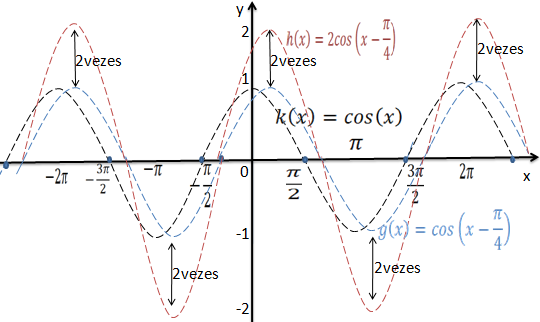
Vamos multiplicar a função g(x)= cos(x+π/4 ) por 2 e assim teremos a função h(x)=2cos(x+π/4 )
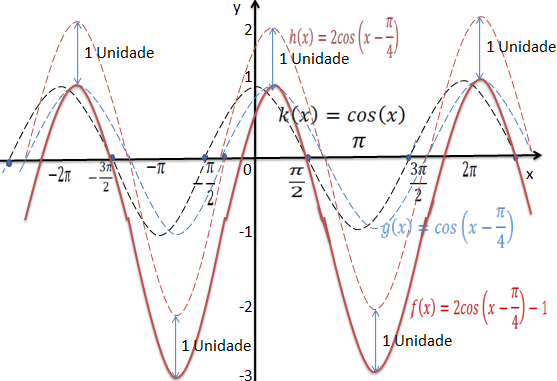
Vamos transladar uma unidade para baixo e assim temos a função f(x)=2cos(x- π/4)-1 a partir da função h(x)=2cos(x- π/4)
Exercícios sobre funções trigonométricas para praticar
Represente graficamente as seguintes funções trigonométricas e fazer o estudo completo para cada uma delas
a)y=cos(x)
c)y=cos(x- π/6)
c)y=-3cos(x)+3
d)y=cos(x)-2
e)y=3cos(x+ π)-2
Veja mais sobre as trigonometria
*Função trigonométrica seno y=sen(x)
*Trigonometria no triângulo rectângulo
*Derivada de funções trigonométricas