Funções trigonométricas
As principais funções trigonométricas são função seno, função cosseno, função tangente e a função co-tangente. Nesse capítulo iremos aprender a como representar graficamente essas funções, e depois dessa secção iremos aprender a representar as suas inversas
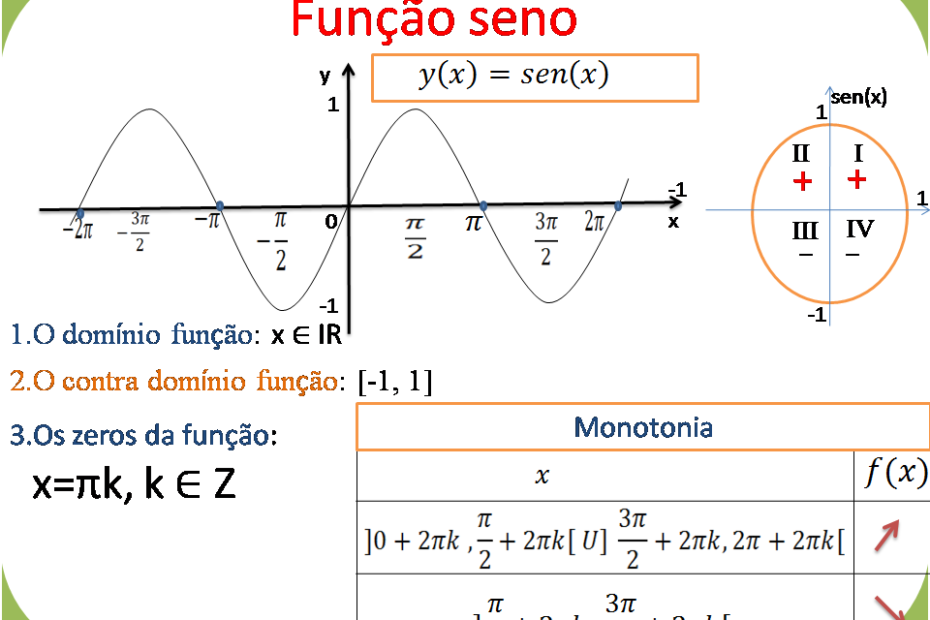
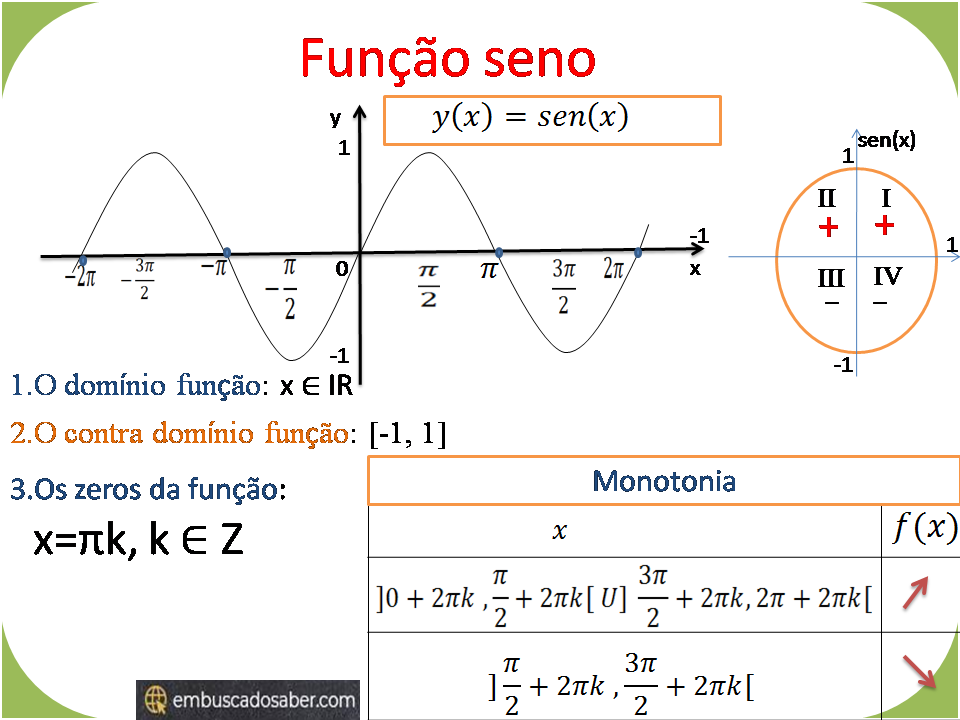
Função seno
Representação gráfica da função y=sen(x)
Para representar o gráfico da função seno iremos construir uma tabela onde atribuiremos valores e x e encontrares com base nesses valores o valor de y.
| x | y=sen(x) |
| 0 | 0 |
| π/2 | 1 |
| π | 0 |
| 3π/2 | -1 |
| 2π | 0 |
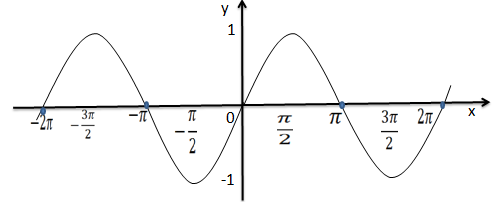
Estudo completo da função trigonométrica y=sen(x)
Dominio: x ∈ R
Contra domínio: y ∈ [-1,1]
Paridade: Impar
Zeros: x=πk, sendo que k ∈ Z
Máximos: x=π/2+2πk,sendo que k ∈ Z
Mínimos: : x=3π/2+2πk,sendo que k ∈ Z
Monotonia

Variação do sinal

Representação gráfica da função f(x)=sen(x+b)
Esse tipo de função é feito a partir da função g(x)=sen(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=sen(x+b) a partir da função g(x)=sen(x) vamos;
– Deslocar b unidades para esquerda se b for positivo
– Deslocar b unidades para directa se b for negativo
Representação gráfica da função f(x)=sen(x)+c
Esse tipo de função é feito a partir da função g(x)= sen(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=sen(x)+c a partir da função g(x)= sen(x) iremos;
– Transladas a função f(x) b unidades para cima se b for positivo
– Transladas a função f(x)b unidades para baixo se b for negativo
Representação gráfica da função y=asen(x)
Esse tipo de função é feito a partir da função g(x)= sen(x), recorrendo ao processo de translação,
Para fazer o gráfico da função f(x)=sen(x)+c a partir da função g(x)= sen(x) vamos;
– Multiplicar por a os valores de y= sen(x). Assim sendo a amplitude da função f(x)=asen(x) será [-a,a].
Exercícios resolvidos para fazer gráficos de funções trigonométricas
1.Represente graficamente a função y=sen(x)+2, e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
Primeiro vamos construir o gráfico da função g(x)=sen(x)
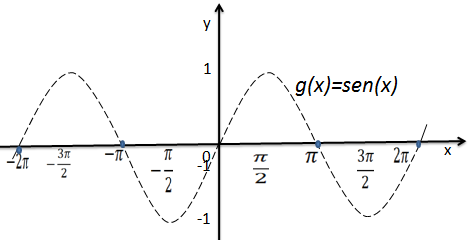
Vamos transladar duas unidades para cima e assim temos a função f(x)=sen(x)+2 a partir da função g(x)=sen(x)
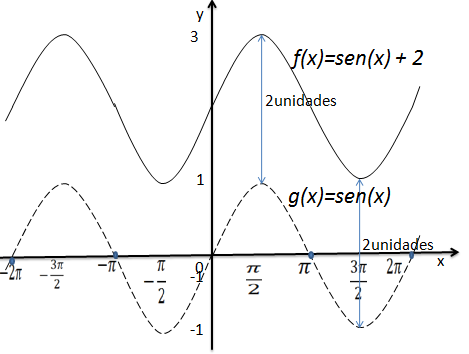
a) O domínio da função é R
b) O contradomínio é [1,3]
c) A ordenada na origem conforme podemos ver no gráfico é y=2.
d) A função em nenhum momento intercepta o eixo das abcissas, logo a função não tem zeros.
2. Esboce o gráfico da função trigonométrica f(x)=2sen(x), e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
Primeiro vamos construir o gráfico da função g(x)=sen(x)

Agora para termos a função f(x)=2sen(x) vamos multiplicar por 2 os valores de y=sen(x) assim os extremos passarão a ser 2•(-1)=-2 e 2•1=2 assim sendo o gráfico da função f(x)=2sen(x) é:
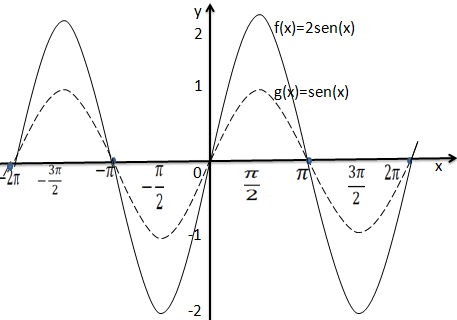
a) O domínio da função é R
b) O contradomínio é [-2,2]
c) A ordenada na origem conforme podemos ver no gráfico é y=0.
d) A função intercepta o eixo das abcissas de π em π , logo a função podemos dizer que os zeros são; x=πk, sendo que k ∈ Z
3.Represente graficamente a função y=sen(x+π /2), e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
Primeiro vamos construir o gráfico da função g(x)=sen(x)

Vamos transladar π /2 unidades para esquerda e assim temos a função f(x)=sen(x+π /2) a partir da função g(x)=sen(x)
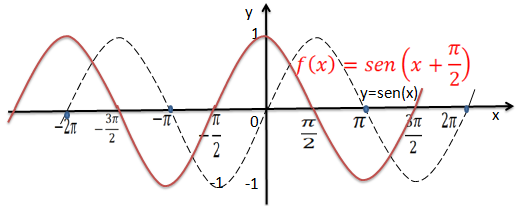
4.Represente graficamente a função y=sen(x-π /2), e indicar;
a) O domínio
b)O contradomínio
c)A ordenada na origem
d)Os zeros
Primeiro vamos construir o gráfico da função g(x)=sen(x)

Vamos transladar π /2 unidades para direita e assim temos a função f(x)=sen(x-π /2) a partir da função g(x)=sen(x)
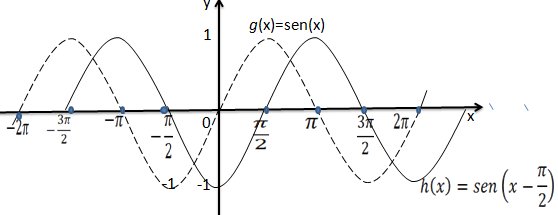
Vamos multiplicar a função h(x) por 0.5

Exercícios para praticar
Represente graficamente as seguintes funções trigonométricas e fazer o estudo completo para cada uma delas
a)y=sen(x)
c)y=sen(x-45)
c)y=sen(x)+3
d)y=sen(x)-2
e)y=sen(x+ π)-1
Veja mais sobre as trigonometria
*Função trigonométrica seno y=sen(x)
*Trigonometria no triângulo rectângulo
*Derivada de funções trigonométricas
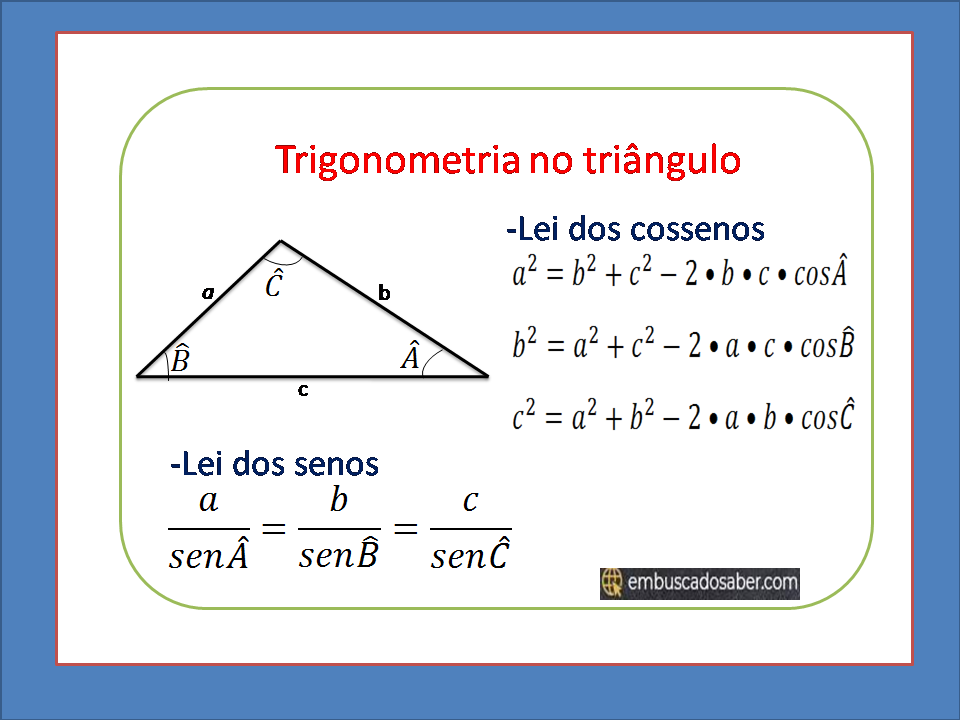
lei dos cossenos e lei dos senos
Lei dos cossenos Seja da um triângulo A lei dos cossenos relaciona os lados desse triângulo e os âng…
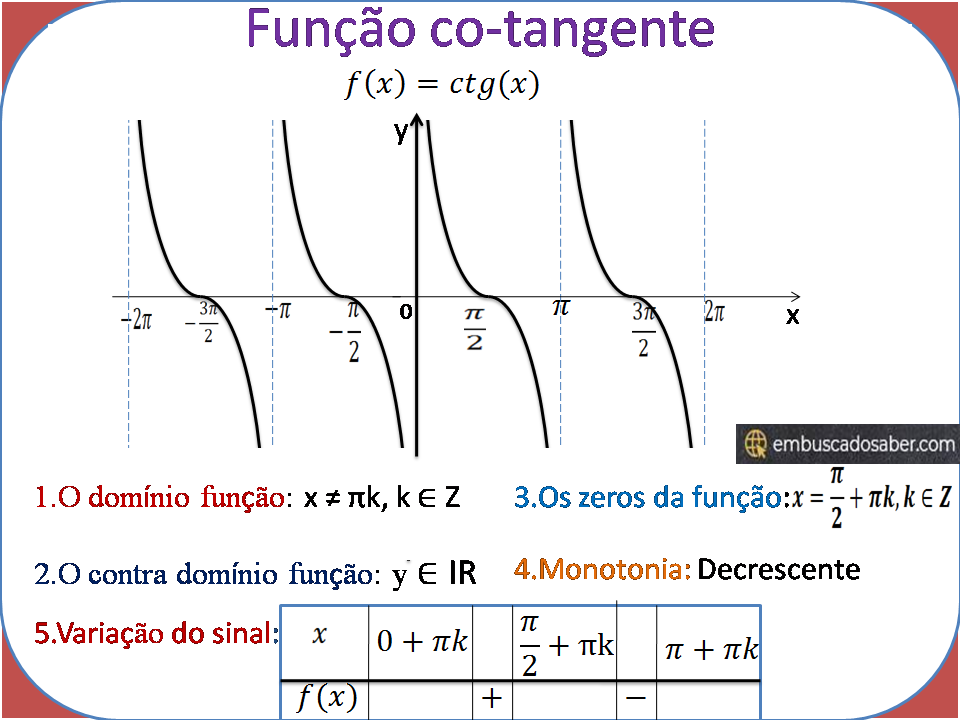
Funções trigonométricas função co-tangente
Funções trigonométricas função co-tangente y=ctg(x) A função co-tangente f(x)= ctg(x) é definida com…
Funções trigonométricas função tangente
Função tangente A função tangente f(x)=tan(x) é definida como a razão entre a função g(x)=sen(x) e a…
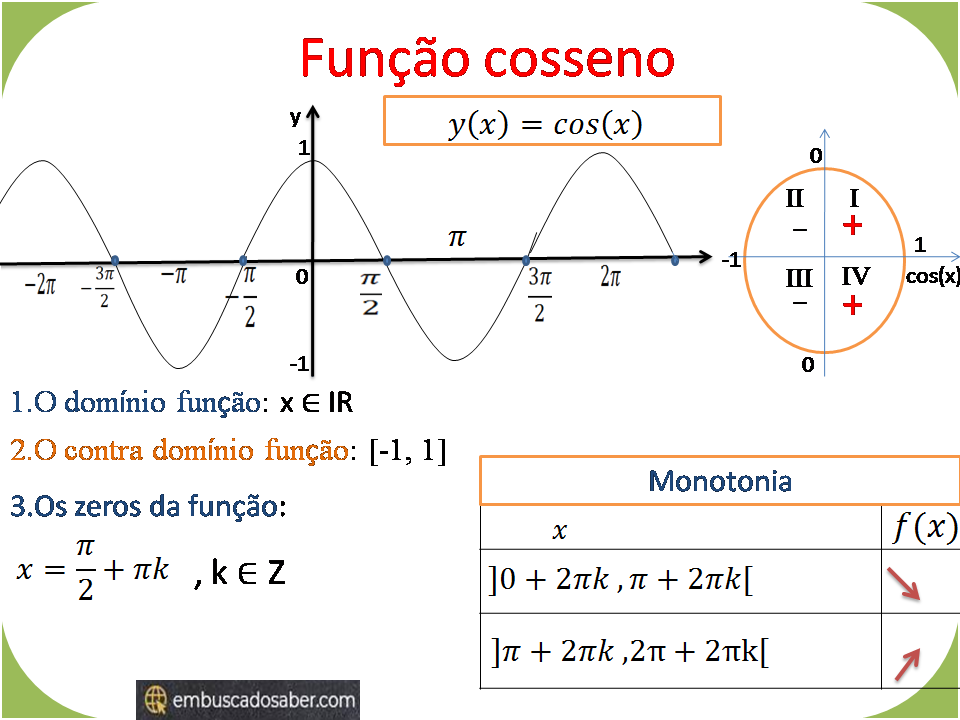
Funções trigonométricas função cosseno y=cos(x)
Função cosseno y=cos(x) Representação gráfica da função y=cos(x) Para representar o gráfico da funçã…
Funções trigonométricas função seno y=sen(x)
Funções trigonométricas As principais funções trigonométricas são função seno, função cosseno, funçã…
Resolução do exame de admissão ao ifp 2023
Acompanhe a resolução do exame de matemática admissão ao Instituto de formação de professores (IFP) …
Manual de preparação para exames de admissão de matemática ao IFP ano lectivo de 2024
Temos manual de preparação para exames de admissão de matemática ao IFP para o ano lectivo de 2024. …
Generalidades em equações paramétricas
Generalidades em equações paramétricas Podemos ter casos complexos em que o parâmetro se transforme …
Equações paramétricas
O que é uma Equações paramétricas ? Denomina-se por equação paramétrica a toda equação quadrática qu…
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Equações Lineares ou equação do 1º grau
Equação linear ou equação do 1º grau é toda a equação do tipo ax+b=0 onde: a é o coeficiente de x e…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …
Exercícios sobre limites e continuidades
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que:Como os limites …
Limites indeterminações do tipo zero sobre zero
Limites contendo indeterminações do tipo zero sobre zero são limites em que ao substituir a var…
Resolução de exercícios sobre limites trigonométricos
Uma vez que já vimos o limite trigonométrico fundamental a gora e a hora de usar esse conhecimentos …
Limites laterais (Limite lateral à esquerda e limite lateral à direita)
Seja dado uma função f(x) cujo o gráfico é representado na figura acima Como achar os limites latera…
As bolas do mundial 2022 são recarregadas?
A bola do mundial 2022 tem um sensor de toque e movimento dentro dela, com o objectivo de fornecer i…
Movimento uniformemente variado
O que é movimento uniformemente variado Movimento uniformemente variado é aquele em que a veloc…
Movimento uniforme
Movimento uniforme Movimento uniforme é aquele em que a velocidade instantânea permanece c…
Queda livre e lançamento vertical para baixo e para cima
Queda livre Durante a queda livre os corpos realizam um movimente uniformemente variado com uma acel…
Lançamento oblíquo
Lançamento oblíquo Para melhor compreende esse movimento vamos analisar o seguinte esquema de um cor…
Lançamento horizontal
O que é lançamento horizontal O lançamento horizontal é um caso particular do lançamento oblíquo. Ne…