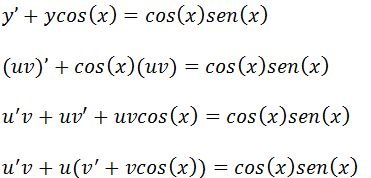Integral de fracções fraccionarias

Integral de funções do tipo

Para integramos essa função vamos transformar a expressão que esta na raiz numa expressão do tipo

Tendo já as integrais nesse formula vamos recorrer as formulas de integrais que fracções para integrais essas fracções de forma imediata;

Como para as nossas integrais u=x+m onde tem u substituiremos por x+m ;

Exercícios Integral de funções com fracções irracionais

Podemos colocar o numerados como uma soma de quadrados da seguinte forma;

x²-4x+8=x²-2•2x+8= x²-2•2x+2²-2²+8=(x-2)²+2² vamos substituir o numerador por essa expressão;

Usando as formulas que aprendemos acima temos;

Fazendo o completamente de quadrado temos x²+6x-16=x²+2•3x-16= x2+2•3x+3²-3²-16=(x+3)²-5²

De acordo com a formula que vimos no inicio da alua essa integral tem como resultado a função logarítmica

Multiplicando o 2 e 5 temos 10 e dessa forma temos concluindo o calculo da nossa integral fraccionaria

Inicialmente colocaremos o 2 em envidaria no denominador

Agora faremos a divisão de 10 e 2 que tem como resultado 5 e tiraremos o 5 para fora da integral

Transformaremos o denominador em uma diferença de quadrados

-x²+8x+20=-(x²-8x-20)= -(x²-2•4x+4²-4²-20)=-((x+4)²-36)=-( x+4)²+6²

vamos substituir na nossa integral o -x²+8x+20 por -( x+4)²+6² e assim temos;

Vamos evidenciar o menos no denominador e tirar para fora da integral

Essa integral tem como resultado a função logaritmo

Primeiro colocaremos o x⁴ na forma de (x²)²

Vamos aplicar uma substituição para reduzir o grão de denominar e assim transformar a integral em outra mais simples

x²=t

2xdx=dt

xdx=dt/2

Transformaremos o denominador em uma soma de quadrados fazendo o complemento de quadrados

t²+10t+34= t² +2•10t+5²-5²+34=(t+5)²+3²

Essa Integral de acordo com as formulas de integrais de funções fraccionarias tem como resultado função arctangente

vamos substituir t por x² uma veis que quando fizemos a nossa substituição dissemos que t=x²

Integrais de funções com fracções onde o denominador é uma equação quadrática

Como calcular essas integrais fraccionarias

Para integral uma função onde o numerador é uma função linear e o de denominador é uma função quadrática temos que fazer operações matemáticas de modo que no numerador tenhamos a derivada do denominador somado a uma conteste (um numero) depois separar a fracção em duas fracções onde uma das fracções é uma fracção onde o numerador é a derivada do denominador.

Temos que dar um fazer operações de modo que no numerador tenhamos 2x+b+k, e depois separar a fracção em duas onde a primeira fracção será (2x+b) /(x²+bx+c) e a segunda fracção será k/(x²+bx+c) .

Primeiramente vamos multiplicar o numerador por 2 e a integral por (1/2)

Vamos separa a nossa integral em duas como dissemos a primeira fracção será (2x+b)/(x²+bx+c) e a segunda fracção o estante.

Vamos distribuir o 1/2 e resolver caca uma das integrais

Exercício sobre Integrais de funções com fracções onde o denominador é uma função quadrática e o numerador função linear

Como queremos ter na derivada do denominador no numerador primeiro vamos multiplicar o numerador por 2

O -6 pode ser colocado como 4-10

Por conseguinte separemos a a nossa integral em duas integrais

Vamos distribuir o 1/2

Iremos calcular parcialmente cada integral

Agora substituiremos a expressão de I₁ e I₂ na nossa integral principal

Com forme os nossos cálculos a nossa integral tem como resposta;

Vamos evidenciar o 4 no denominador tirar fora da integral

Evidenciaremos o3 no numerador e tiraremos para fora da integral por ser uma contaste

Multiplicaremos o numerador por -2 e multiplicaremos a integral por (-1/2)

Vamos adicionar o 8-8 no numerador para podemos ter o 2x+8 no numerador que é a derivada do denominador

Vamos separa a integral em duas integrais depois integraremos cada uma das fracções

Aplicaremos a propriedade distributiva e Distribuiremos -3/ 8

Calcularemos separadamente I₁ e I₂

Vamos substituir essas soluções de I₁ e I₂ na nossa integral principal

Multiplicando o 3/ 2 e 1/12 temos 1/8

A solução da nossa integral e’:

Mas aulas

• Integral de uma função polinomial

• Integral de uma função exponencial

• Integral de funções que resulta em uma função logaritmo

• Integral da função trigonométrica

• Integral usando o método de substituição

• Integrais por partes