Integral de funções trigonométricas seno e cosseno

Como integral uma função trigonométrica seno?

As funções trigonométricas são funções com muita aplicação, saber calcular suas integrai ira nos ajudar a resolver diversos problemas na vida pratica e em problemas de calculo e não só, veja abaixo as formulas para calcular a integral da função sen(x) e da função cos(x);

Fórmula de Integral de uma função trigonométrica seno e cosseno

∫ sen(x) dx = –cos(x)+c

∫ cos(x) dx = sen(x)+c

Demonstração da integral da função trigonométrica seno

Para chegarmos a fórmula da Integral de uma função trigonométrica seno devemos parte do conhecimento da derivada das funções trigonométricas seno e cosseno onde vimos que a derivada de y=cos(x) é y’=-sen(x) o que significa que a integral de –sen(x) é cos(x) escrevendo isso de usando o símbolo de integral temos;

∫-sen(x) dx=cos(x)

Vamos agora multiplicar ambos membros por -1 de modo que na nossa integral fiquemos apenas com sen(x), fazendo esse processo temos;

∫sen(x) dx=-cos(x)

E como sempre quando integramos temos que depois colocar mais uma constante para generalizar a solução.

∫sen(x) dx=-cos(x)+c

Onde o é “c” nosso constante de integração

Demonstração da integral da função trigonométrica cosseno

A demonstração da integral da função trigonométrica cosseno é feita de forma análoga a Integral da função seno, basta recordar que a derivada da função seno é a função cosseno o que quer dizer que a integral de cosseno é a função seno.

∫cos(x)dx=sen(x)

Devemos colocar a nossa constante de integração para generalizar a integral

∫cos(x)dx=sen(x) + c

Propriedades do cálculo integral de uma função trigonométrica

* Como integral uma função do tipo ∫ cos(ax+b)dx

Se desejássemos a derivada seria a derivada de cosseno com argumento “(ax+b)” multiplicado por “a” então nesse caso de integral será a integral de cosseno que é seno com argumento (ax+b) dividido por “a” ou seja :

A integral de uma função trigonométrica do tipo cos(ax+b) é sen(ax+b) dividido por “a” .

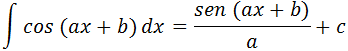
* Como integral uma função do tipo ∫ sen(ax+b)dx

Seguindo a mesma linha de pensamos explicado acima A integral de uma função trigonométrica do tipo sem (ax+b) é -cos(ax+b) dividido por “a” .

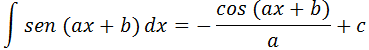
Usando as propriedades acima sobre integrais trigonométricos calcule as seguintes integral

a) calcule a seguinte integral trigonométrica; ∫sen(2x+3) dx

Conforma já sabemos a integral de seno é cosseno e como se fosse para derivar iríamos multiplicar pelo valor que esta antes do x , aqui como é integral iremos dividir per esse numero.

Seguindo a mesma formula de integrais trigonométricas tendo em conta que o nosso a=5/7

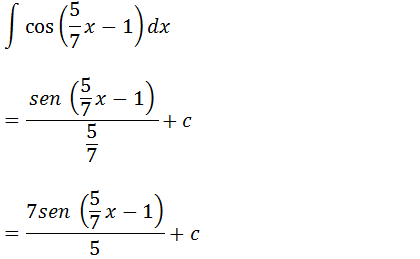
c)Achar o solução da seguinte integral ∫sen(-9x)dx

d) Calcular a seguinte integral ∫cos(4x) dx

A integral de ∫cos(4x) é sen(4x) dividido por 4.

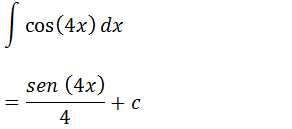
e) Encontrar a solução de ;∫sen(-x) dx

Vamos integral essa função trigonométrica de forma análoga ao anteriores exercícios tendo em conta que agora o valor que esta antes do x é -1.

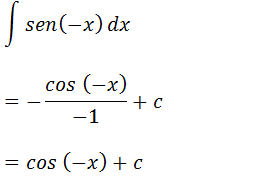
f) Calcular a seguinte integral ; ∫sen(2) dx

sen(2) É uma constante e para integral uma constante em relação a x basta multiplicar a constante por x.

∫sen(2) dx

=sen(2)x+c

Veja mais aulas sobre trigonométrica

• Trigonometria no triângulo rectângulo
• lei dos cossenos e lei dos senos
• Equações trigonométricas
• Funções trigonométricas função co-tangente

• Funções trigonométricas função tangente
• Gráficos de funções trigonométricas função cosseno y=cos(x)
• Funções trigonométricas função seno y=sen(x)
• Derivada de funções trigonométricas seno e cosseno
• Derivada de funções trigonométricas tangente e co-tangente
• Limite trigonométrico
• Resolução de exercícios sobre limites trigonométricos

Veja essa aula em video