Integral de funções que resultam em arctag(x)

Essa é uma integral imediata, bastando apenas nos recordar da derivada da função arctangente (a função arctan(x)) , Quando aprendemos derivada vimos que a derivada da função arctan(x) é a função 1/(x2+1), O que pelo conceito de integral quer dizer que a integral da função 1/(x2+1) é a função arctan(x) e podemos escrever usando o símbolo de integral como sendo;
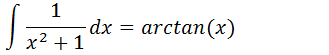
Sempre tivermos uma integral definida no fim depois de achar a solução devemos adicionar uma contaste arbitraria para generalizar a nossa solução vamos adicionar a contaste a nossa solução
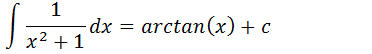
Usando as formulas aprendidas anteriormente
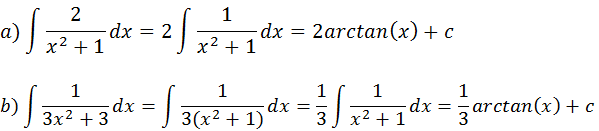
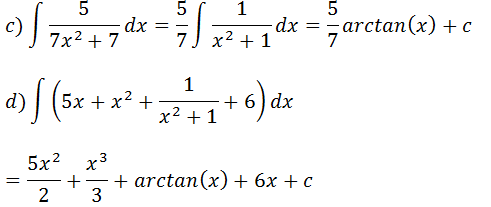
Formula generalizada da integral que resultam em arctangente
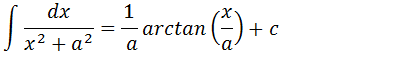
Demonstração da formula
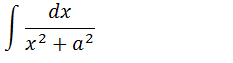
Iremos transformar a nossa fracção em uma função onde no numerador temos u2+1 para podemos aplicar que a integral se transforme em uma integral ja conhecida para isso vamos evidenciar o “a” no denominador
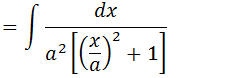
Recorrendo ao método de substituição, onde substituiremos x/ a por u
x/a=u
x=au
dx=adu
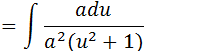
Vamos simplificar o “a2” do numerador com um “a” do denominar e depois tirar o “a” que sobra no denominar para fora da integral
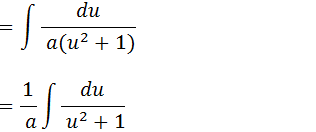
Sabemos que a integral de 1 sobre u2+1 tem como resultado arctan(u)
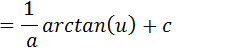
Vamos substituir u por x/a e assim temos demonstração
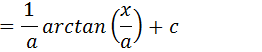
Exercícios de calculo de integrais que resultam em funções trigonométricas inversas arcseno
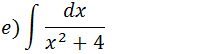
Colocando o 4 em forma de potencia de expoente 2

Usando a forma que aprendemos acima temos como solução
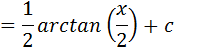
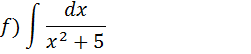
Vamos colocar cinco na raiz e elevar ao quadrado
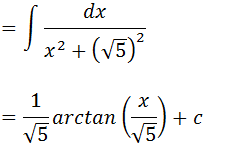
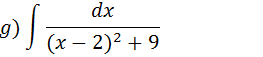
Podemos colocar 9 como 32
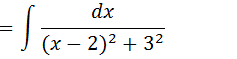
Seja ; x-2=u
dx=du
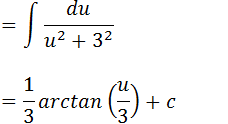
Como dissemos que u=x-2 onde tem u iremos substituir por x-2
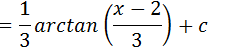
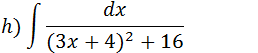
Podemos escrever 16 como sendo 42
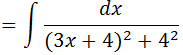
Fazendo; 3x+4=u
3dx=du
dx=du/3
Substituindo na nossa integral temos;
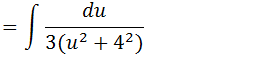
Tirando o 3 para fora da integrar
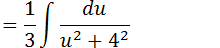
Essa integral tem como resultado a função arctagente
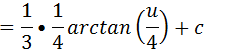
Podemos multiplicar 3 e 4 e assim temos o resultado final da nossa integral
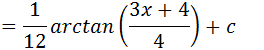
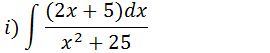
Vamos separa a nossa integral em duas integrais
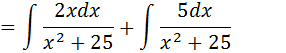
A primeira integra é uma integral do tipo du/u que resulta em ln|u| onde o nosso u é x2+25 e a segunda integral tem como em arctagente, mais na segunda primeiramente vamos tirar o 5 para fora da integral transformar 25 em 5 ao quadrado;
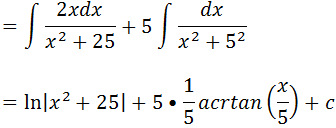
Fazendo a simplificação temos
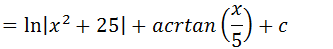
Integrais com fracções de uma diferença de quadrados no denominador
Integrais com fracções do tipo
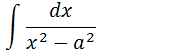
Essa integral tem como resultado;
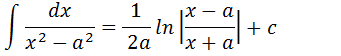
Demonstração da integral com fracções
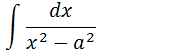
Quando aprendemos casos notáveis vimos que x2-a2=(x-a)(x+a)
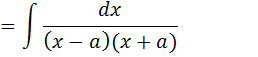
Vamos trabalhar com a fracção que esta dentro da integral separar ela em duas fracções
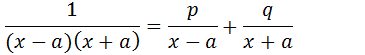
Vamos calcular o valor de “p” e “q”
1=p(x+a)+q(x-a)
1=px+pa+qx-qa
1=(p+q)x+pa-qa
p+q=0 e pa-qa=1
p=- q
-qa-qa=1
-2qa=1
q=-1/2a
p=-q=1/2a
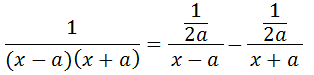
Vamos colocar o “1/2a” em envidecia
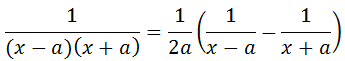
Vamos substituir essa espressao na nossa integral
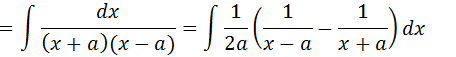
Vamos tira o “1/2a” para fora da integral e separa a nossa integral em duas integrais
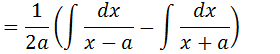
Sabemos que integral de 1/u é igual a ln|u| onde para a primeira integral o nosso u é “x-a” e para a segunda integral o u e’ “x+a”
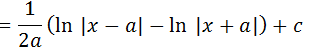
Aplicando a propriedades de diferença de logaritmos temos;
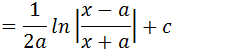
Exercícios para praticar integrais com fracções

Vamos colocar o denominador na formula x2-a2 , onde para isso vamos transformar 9 em 32
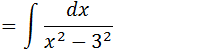
Usando a formula que aprendemos acima temos

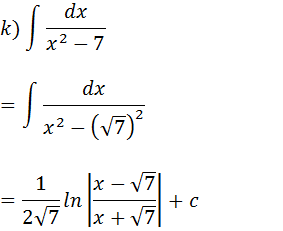
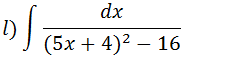
Vamos substituir 16 por 42
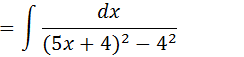
Usaremos o método de substituição
Seja ; 5x+4=u
5dx=du
dx=du/5
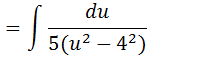
Vamos tira o 5 para fora da integral e depois aplicar a nossa formula de integrais com fracções
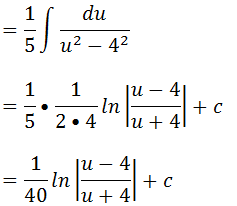
Como u=5x+4 vamos substituir u por essa expressão
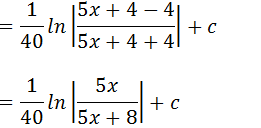
Aulas relacionadas
- Calculo integral
- Derivada de arctan
- Derivada de funções logaritmos
- Integral de funções exponencial
- Derivada de funções trigonométricas
- Limites trigonométricos
Resolução do exame de admissão ao ifp 2023
Acompanhe a resolução do exame de matemática admissão ao Instituto de formação de professores (IFP) …
Manual de preparação para exames de admissão de matemática ao IFP ano lectivo de 2024
Temos manual de preparação para exames de admissão de matemática ao IFP para o ano lectivo de 2024. …
Generalidades em equações paramétricas
Generalidades em equações paramétricas Podemos ter casos complexos em que o parâmetro se transforme …
Equações paramétricas
O que é uma Equações paramétricas ? Denomina-se por equação paramétrica a toda equação quadrática qu…
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Equações Lineares ou equação do 1º grau
Equação linear ou equação do 1º grau é toda a equação do tipo ax+b=0 onde: a é o coeficiente de x e…
Contradomínio de funções trigonométricas
Como encontrar o contradomínio de uma função trigonométrica? Para encontrar o contradomínio das funç…
Método de adição ordenada
Resolução de sistema de equações usando o Método de adição ordenada Vamos aprender como resolver sis…
Resolução de sistema de equações
Sistema de equações com duas variáveis Vamos aprender como resolver sistemas de equações com duas va…
Fórmula para encontrar números primo
Será que existe uma fórmula para encontrar um número primo? Muitos acreditam que não existe uma form…
Equações irracionais
o que são equações irracionais Equações irracionais são equações que contem uma expressão irracional…
Números primos
O que são números primos? Número primos são números naturais com apenas dois divisores o 1 e o própr…
Propriedades de potência
Quais são as propriedades de potência Existem diversas propriedades de potência iremos nos centrar n…
Quadrado de uma soma e quadrado de uma diferença
Quadrado de uma soma Quadrado de uma soma é uma expressão matemática do tipo: (a+b)2 O quadrado de u…
Livro de calculo integral
Livro de calculo Integral Caso você queira aprender calculo integral recomendamos a você adquirir o …
Números complexos
Números complexos (C) Os números complexos são representados pelo conjunto C, nesse conjunto encontr…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
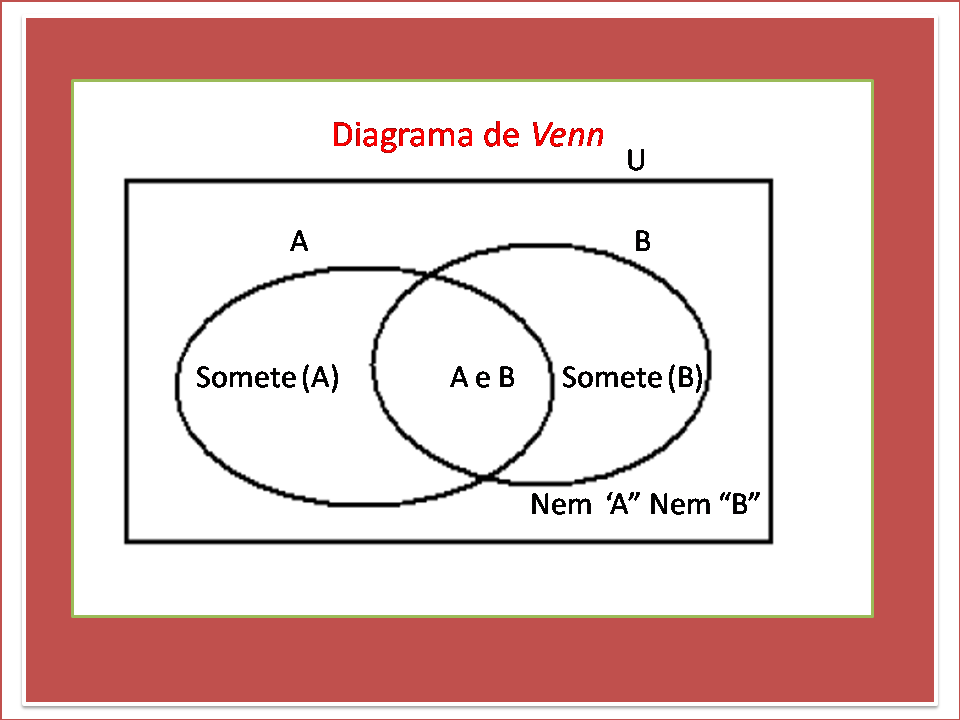
Diagrama de Venn
O que é diagrama de Venn O diagrama de Venn é uma forma Matemática usada para representar um conjunt…
Integral de fracções fraccionarias
Integral de funções do tipo Para integramos essa função vamos transformar a expressão que esta na ra…
Integral de funções com fracções
Integral de funções que resultam em arctag(x) Essa é uma integral imediata, bastando apenas nos reco…
Integral de funções com fracções ( com raiz no denominador)
Integral de fracções com raiz no denominador Primeiro tipo Para integramos essa função vamos transfo…
Integral de funções que resultam em arcseno
Vamos começar o estudo da Integral de funções com fracções, primeiramente vamos aprender funções bem…
Integrais por partes (calculo integral usando o método de integrais por partes)
Integrais por partes A técnica de Integral por partes é uma técnica usada para simplificar a resoluç…
Integral usando o método de substituição
Usar uma substituição no cálculo integral torna-se indispensável para resolver diversos exercícios d…
Integral de funções trigonométricas seno e cosseno
Como integral uma função trigonométrica seno? As funções trigonométricas são funções com muita aplic…
Integral de funções que resulta em uma função logaritmo
Como integral uma função do tipo? Como forma de introdução e para facilitar a nossa compressão nessa…
Integral de uma função exponencial
Como integral uma função exponencial? Se você já se perguntou como integral uma função exponencial n…
Cálculo integral
Calculo de integrais de funções tipo ∫ xn dx Tendo já com alguma noção de o que seja o cálculo integ…
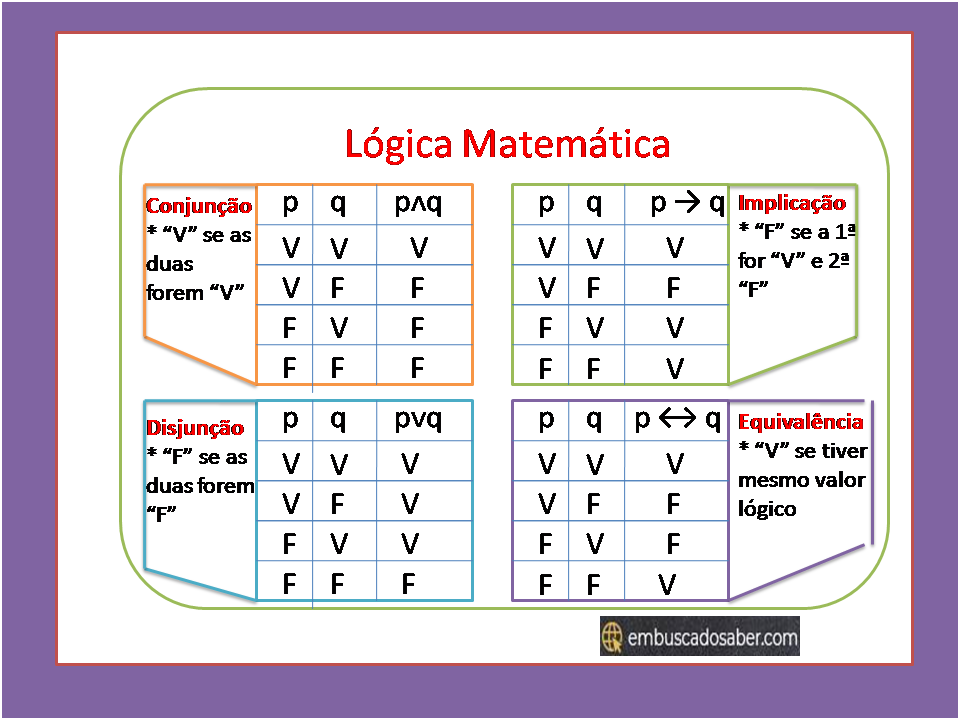
Lógica Matemática ( operações lógicas e proposições)
Lógica Matemática A lógica matemática estuda o raciocínio matemático Valor lógico Os valores lógicos…
Tipos de conjuntos (Teoria de conjuntos)
O que é um conjunto ? Conjunto é um agrupamento que pode ser de seres, números objectos etc, com as …