Integral usando o método de substituição

Usar uma substituição no cálculo integral torna-se indispensável para resolver diversos exercícios de cálculo integral. Em alguns casos pode ser opcional usar o método de substituição, mais em outros casos devido a complexidade do exercício usar o método de substituição torna-se o método mais pratico para resolver o exercício.

∫ (x+2)² dx

=∫ (x²+4x+4)dx

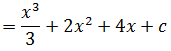
Agora vamos imaginar se o expoente fosse 100

∫ (x+2)¹⁰⁰dx

Com expoente 100 fica muito trabalhoso desfazer a potência, pois teremos muito termo ( 101 termos) sem cotar que para encontrar esses termos teremos que perder muito tempo, gastar muito espanco a escrever cada termo.

Imagina de fosse em víeis de x+2 tivéssemos u ou seja se fosse ∫ u ¹⁰⁰ dx ai já teríamos uma integral muito simples de calcular, o método de substituição é exactamente isso transformar uma integral aparentemente complicada ou trabalhosa em uma integral simples

∫ (x+2)¹⁰⁰dx

u=x+2

du=dx

∫ u¹⁰⁰du

Vamos recordar que u=x+2 vamos substituir o u por x+2 e assim temos o resultando da nossa integral

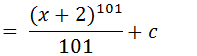
Agora que ja temos a integral inicial de calculo integral vamos continuar resolvendo exercício

Resolução de exercício de calculo integral usando o método de substituição

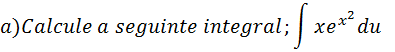
Seja: x²=u

2xdx=du

b)Calcule a seguinte integral; ∫ 6x²cos(x³) dx

∫ 6x²cos(x³) dx

x³=u

3x²=du

x² dx=du_/3 , colocando na nossa integral temos;

=∫6cos(u)du_/3

=∫2cos(u)du

=2sen(u)+c

=2sen(x³)+c

c) Calcule a seguinte integral: ∫ sen(x)cos²(x) dx

Para resolver essa integral vamos usar o método de substituição

∫sen(x)cos²(x)dx

cos(x)=u

-sen(x)dx=du

sen(x)dx=-du

=-∫u²dx

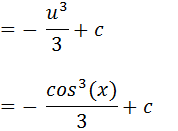
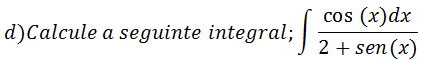
Vamos aplicar o método de substituição :

seja: 2+sen(x)=u

cos(x)dx=du

=ln|u|+c

=ln|2+sen(x)|+c

e)Calcule a seguinte integral; ∫ tag(x) dx

A função tangente e’ a razão da entre a função seno e a função cosseno , vamos substituir tan(x) por sen(x)/ cos(x) e depois aplicar o método de substituição.

∫ tag(x) dx

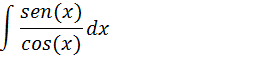
cos(x)=u

-sen(x)dx=du

sen(x)dx=-du

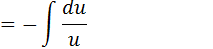
=-ln|u|+c

=-ln|cos(x)|+c

f)Calcule a seguinte integral; ∫ ctg(x) dx

A função co-tangente e’ a razão da entre a função cosseno e a função seno , vamos substituir ctg(x) por cos(x)/ sen(x) e depois aplicar o método de substituição.

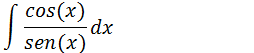
sen(x)=u

cos(x)dx=du

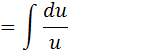
=ln|u|+c

=ln|sen(x)|+c

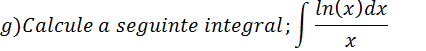
Seja: ln|x|=u

Substituindo na expressão da nossa integral temos;

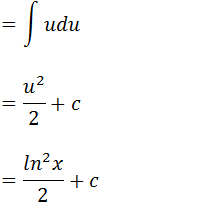
h) Encontrar a solução da seguinte integral; ∫x⁴(x⁵+8)⁹dx

∫x⁴(x⁵+8)⁹dx

x⁵ +8=u

5x⁴dx=du

x⁴=du/5

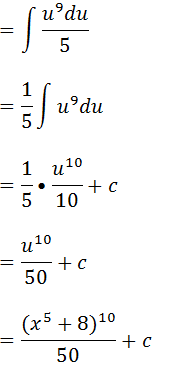
Veja a aula em video

Aulas relacionadas

• Calculo integral
• Integral de funções exponencial
• Integrais que resultam em logaritmo
• derivada de funções trigonométricas